Segment Tree 线段树算法
什么是线段树算法:
线段树(Segment Tree)是一种基于树结构的数据结构,用于解决区间查询问题,例如区间最大值、最小值、区间和等。线段树是一种高度平衡的二叉树,每个节点都代表了一个区间。下面我们来详细了解一下线段树算法。
线段树的构建
线段树的构建过程可以通过递归的方式实现。对于一个给定的数组,我们首先构建一个高度为 log n 的线段树,其中 n 是数组的长度。每个节点都代表了一个区间,例如左儿子节点代表[l, r],右儿子节点代表[r+1, r2]。具体的构建过程如下:
1.初始化根节点,区间为[0, n-1]。
2.对于每个节点,如果它的左右儿子节点存在,就递归构建左右儿子节点。
3.每个节点的值根据需要更新,例如查询最大值时,每个节点存储的值应该是该区间内的最大值
4.当构建到叶子节点时,将叶子节点的值存储为对应区间的值。
线段树查询
线段树查询可以通过递归的方式实现。对于一个查询区间[l, r],我们从根节点开始,根据区间与节点所代表区间的关系,逐步向下遍历子树,直到到达叶子节点。在遍历过程中,我们可以根据需要更新节点的值,例如查询最大值时,如果当前节点的值比查询区间的值更大,就将当前节点的值更新为查询区间的值。具体的查询过程如下:
1.从根节点开始,如果当前节点所代表的区间与查询区间有交集,就继续向下遍历。
2.如果当前节点的左儿子节点存在,并且左儿子节点所代表的区间与查询区间有交集,就递归查询左儿子节点。
3.如果当前节点的右
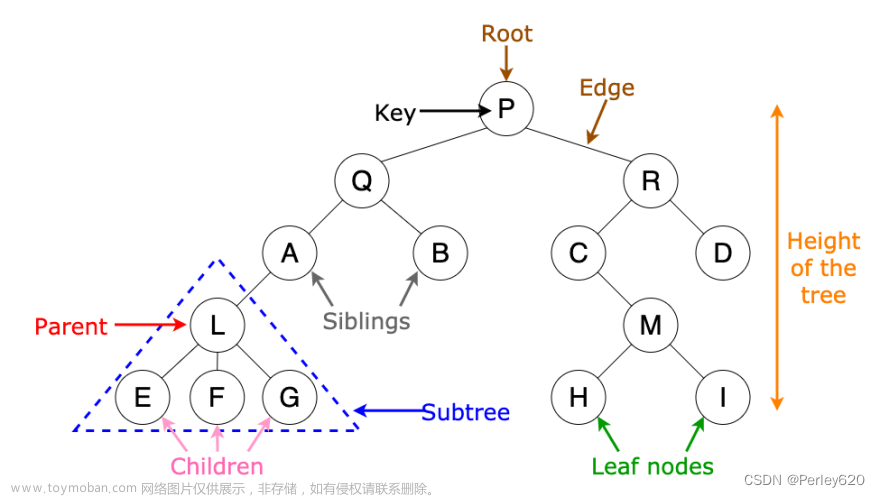
示例1: 线段树是一种二叉搜索树。他将一段区间划分为若干个单位区间,每个节点之间存储一个区间。思想类似于分治思想。
线段树是一种二叉搜索树。他将一段区间划分为若干个单位区间,每个节点之间存储一个区间。思想类似于分治思想。
如图所示,线段树中每一个节点都存储着区间[1,10]中的信息,叶子节点的L = R。大致思想为:将大区间平分为2个小区间,每一个小区间再平分为更小的2个区间,以此类推直到每个区间的L = R,通过对这些区间的修改和查询来实现对大区间的修改和查询。
单点查找、修改的时间复杂度:O(log2n)
线段树维护的问题必须满足区间加法 例如:[1,3] + [2,4] = [1,4]。文章来源:https://www.toymoban.com/news/detail-586433.html
代码演示
public static class SegmentTree{
//记录原数组的长度, 线段树下标是从1 开始,原数组是从0开始,
private int MAXN;
//保存原数组的信息,不过下标从1开始了
private int[]arr;
//模拟线段树维护记录区间和
private int[]sum;
//为累加和懒加载
private int[]lazy;
//区间更新的值
private int[]change;
//是否更新的标记
private boolean[]update;
public SegmentTree(int[] origin) {
MAXN = origin.length + 1;
for (int i = 1; i < MAXN;i++){
arr[i] = origin[i - 1];
}
//用来记录逻辑概念中,某一范围的累加和信息。
sum = new int[MAXN << 2];
//用来支持逻辑概念中,某一个范围沒有往下透传的累加任务
lazy = new int[MAXN << 2];
//用来支持逻辑概念中,某一个范围更新任务,更新成了什么
change = new int[MAXN << 2];
// 用来支持逻辑概念中,某一个范围有没有更新操作的任务
update = new boolean[MAXN << 2];
}
/**
* rt 代表逻辑概念中 所在的位置
* @param rt
*/
public void pushUp(int rt){
sum[rt] = sum[rt << 1] + sum[rt << 1 | 1];
}
/**
* 初始化线段树
* 初始化时 先把sum数组填好
* @param l
* @param r
* @param rt
*/
public void build(int l,int r,int rt){
if (l == r){
sum[rt] = arr[l];
return;
}
int mid = (r + l) >> 1;
build(l,mid,rt << 1);
build(mid + 1,r,rt << 1 | 1);
pushUp(rt);
}
/**
* 任务往下分配
* @param rt 当前位置
* @param ln 分配任务的左边界
* @param rn 分配任务的右边界
*/
private void pushDown(int rt,int ln,int rn){
if (update[rt]){
update[rt << 1] = true;
update[rt << 1 | 1] = true;
change[rt << 1] = change[rt];
change[rt << 1 | 1] = change[rt];
lazy[rt << 1] = 0;
lazy[rt << 1 | 1] = 0;
sum[rt << 1] = change[rt] * ln;
sum[rt << 1 | 1] = change[rt] * rn;
update[rt] = false;
}
//懒加载的数据分发下去
if (lazy[rt] != 0){
lazy[rt << 1] += lazy[rt];
sum[rt << 1] += lazy[rt] * ln;
lazy[rt << 1 | 1] += lazy[rt];
sum[rt << 1 | 1] += lazy[rt] * rn;
lazy[rt] = 0;
}
}
/**
* L - R 任务的范围,C 修改的大小
* l r ,rt 所负责的范围。
* @param L
* @param R
* @param C
* @param l
* @param r
* @param rt
*/
public void add(int L,int R,int C,int l,int r,int rt){
if (L <= l && r <= R){
sum[rt] += C * (r - l + 1);
lazy[rt] += C;
return;
}
int mid = (r + l) >> 1;
//任务没有全包,就下发。
pushDown(rt,mid - l + 1,r - mid);
if (L <= mid){
add(L,R,C,l,mid,rt << 1);
}
if (R > mid){
add(L,R,C,mid + 1,r,rt << 1 | 1);
}
pushUp(rt);
}
/**
* //L - R 范围内所有值都变成 C
* //l - r 是 rt 所在位置的包含数字的范围
* @param L
* @param R
* @param C
* @param l
* @param r
* @param rt
*/
public void update(int L,int R,int C,int l,int r,int rt){
//所在范围被全包了。
if (L <= l && r <= R){
change[rt] = C;
update[rt] = true;
sum[rt] = (r - l + 1) * C;
lazy[rt] = 0;
return ;
}
int mid = (r + l) >> 1;
pushDown(rt,mid - l + 1,r - mid);
if (L <= mid){
update(L,R,C,l,mid ,rt << 1);
}
if (R > mid){
update(L,R,C,mid + 1,r,rt << 1 | 1);
}
pushUp(rt);
}
/**
* 查询
* //L - R 要查询的范围
* //l - r 是 rt 所包含的范围。
* @param L
* @param R
* @param l
* @param r
* @param rt
* @return
*/
public long query(int L,int R,int l,int r,int rt){
if (L <= l && r <= R){
return sum[rt];
}
int mid = (r + l) >> 1;
pushDown(rt,mid - l + 1,r - mid);
long ans = 0;
if (L <= mid){
ans += query(L,R,l,mid,rt << 1);
}
if (R > mid){
ans += query(L,R,mid + 1, r, rt << 1 | 1);
}
return ans;
}
}
蓄水池算法
蓄水池算法文章来源地址https://www.toymoban.com/news/detail-586433.html
到了这里,关于Segment Tree 线段树算法(java)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!