实验内容：
输入：任意的有向图
输出：
1）每个节点的聚集系数
2）每个节点对的邻里重叠度
相关定义介绍：
聚集系数：节点A的聚集系数 = A的任意两个朋友之间也是朋友的概率（即邻居间朋友对的个数除以总对数）
邻里重叠度：与A、B均为邻居的节点数/ 与节点A、B中至少一个为邻居的节点数
实验思路说明：
在有向图中，可能出现自循环和双向边的情况，在计算聚集系数或邻里重叠度的时候，忽略自循环并将双向边视做一条边，因此在代码实现时会根据意义做相应处理。
1.首先创建一个graph类作为有向图的父类：
numberOfVertices():返回顶点总个数
numberOfEdges():返回邻边总条数
existsEdges(int,int):判断某条边是否存在
insertEdge(int,int,int):插入边
easeEdge(int,int):删除某条边
degree(int):计算某点的度数
inDegree(int):计算某点的入度
outDegree(int):计算某点的出度
directed():判断该图是否为有向图
Weighted():判断是否为加权图
2.创建以graph类为基类派生有向图子类adjacencyWDigraph:
因为是有向图，所以某些方法做特殊处理
public属性：
int n;//节点数
int e;//边数
T noEdge;//表示不存在的边
T** a;//邻接矩阵
public方法：
adjacencyWDigraph(int nV = 0, T theNoEdge = 0) ：初始化方法，将邻接矩阵二维数组中的每一条边都置为noEdge。
int numberOfVertices() ：返回顶点个数
int numberOfEdges()：返回边的条数
bool directed() ：判断是否有向，返回true
bool weighted()：判断是否加权
bool existsEdge(int i, int j)：判断（i，j）边是否存在，若查询的边不在邻接矩阵范围之内或者不存在则返回false，否则返回true。
void insertEdge(int v1, int v2, int weight)：插入边，输入要插入边的起点、终点、权重，当顶点不在邻接矩阵范围之内则判定为非法插入。否则判断边（v1,v2）是否存在，不存在则有向图边数加1，并令a[v1][v2] = weight。
void easeEdge(int i, int j)：删除边（i，j），如果该边存在则令a[i][j] = noEdge并让边数减一。
int outDegree(int theV)：计算theV点的出度，使用局部变量sum记录邻接矩阵theV行不为noEdge的数目。
int inDegree(int theV)：计算theV点的入度，使用局部变量sum记录邻接矩阵theV列不为noEdge的数目。
int getFriendsIsFriends(int iE)：返回节点iE任意两个朋友之间也是朋友的数目。在有向图中因为可能存在双向边或自循环，因此在计算iE点的邻边数目（即入度加上出度）时，若存在自循环要减去2以及iE点上双向边的条数；若不存在自循环，则只需要减去双向边条数即可。
大体思路是用friends数据记录iE点的所有朋友（即相邻点），后逐个判断friends数组中某一顶点与其他friends中其他顶点是否为朋友，使用变量friendsIsFriends记录数目并返回。
3.在执行主函数中：
首先创建有向图对象graph并输入邻接矩阵。用string aggCoeff[100]数组来记录每一个顶点的聚集系数。依次对每个顶点进行如下步骤，计算该点的总度数（忽略自循环以及把双向边看作一条边），该点总度数即为该点的朋友总数。
计算聚集系数：
计算聚集系数的分母，即为朋友两两之间能形成连边的总数（可用等差公式）。
分子可用有向类中的getFriendsIsFriends函数得到。
计算聚集系数并把结果记录到aggCoeff数组中的对应顶点编号上。
计算邻里重叠度：
使用degreeEdges数组记录每对顶点之间的邻里重叠度。对每对顶点m、j依次进行以下操作。用getAEdges数组记录与m点邻接的其他顶点，用getBEdges记录与点j邻接的顶点。legA、legB分别记录m、j点的邻边总数（注意自循环和双向边，处理方式同上）
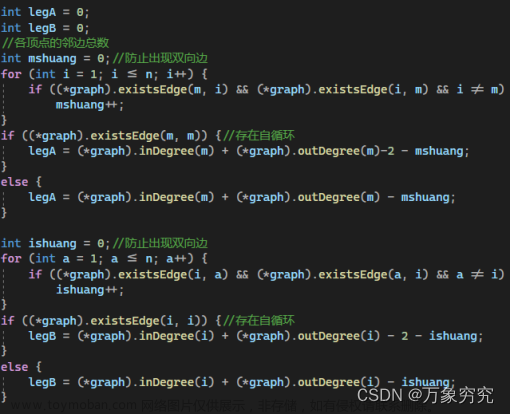
邻里重叠度的分母即为这对顶点的去重复总邻居顶点数，使用自定义getDeno（）函数计算：
如果getAEdges与getBEdges有重复顶点，记录重复顶点数为k。总邻居顶点数为总度数减去重复数。
邻里重叠度的分母为同时是A,也同时是B的邻居的节点个数，使用getCoin（）函数来获取分子，即getAEdges与getBEdges中的重复顶点数。
记录并输出邻里重叠度结果：
程序执行结果：
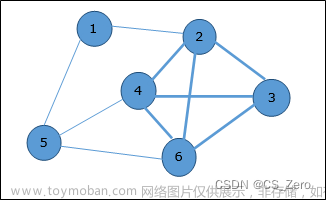
根据上图进行矩阵输入，输出结果如下：
文章来源：https://www.toymoban.com/news/detail-586472.html
以上是鄙人对实验内容的一些粗陋想法，若有不当之处欢迎指正。文章来源地址https://www.toymoban.com/news/detail-586472.html
到了这里，关于众智科学：计算聚集系数和邻里重叠度的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
![[QT编程系列-32]：科学计算 - QT支持的科学计算库](https://imgs.yssmx.com/Uploads/2024/02/604929-1.png)
