【KMP算法简介】
KMP算法中的next数组仅取决于模式串本身,而与相匹配的主串无关。
KMP算法中的next数组,是KMP算法的核心。
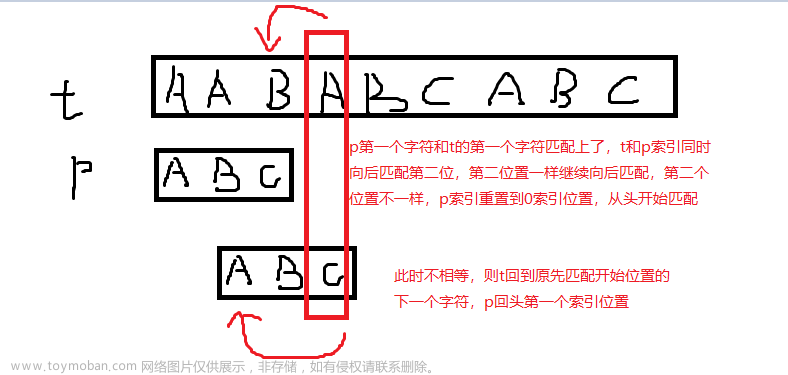
KMP算法是由克努特(Knuth)、莫里斯(Morris)和普拉特(Pratt)共同设计实现的,因此简称KMP算法。此算法可以在O(n+m)的时间数量级上完成串的模式匹配操作。其相对于BF算法的改进在于:每当失配时,无须回溯主串的指针,而是利用已经得到的“部分匹配”的结果将模式串向右“滑动”尽可能远的一段距离后,继续进行比较。这个滑动的距离就是由next数组确定的。
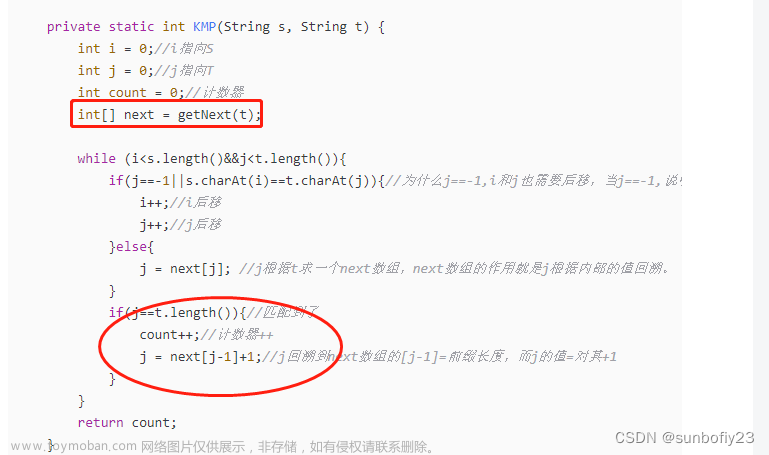
KMP算法本身并不复杂,主要分为两步:求next[ ]数组、匹配字符串。但绝大部分的文章把它讲混乱了,以致造成很多混淆。
【求next数组的算法】
求next数组 在KMP算法的众多实现中,有许多种定义next数组的方式。所以在使用和查看别人代码时,要特别注意KMP算法的next数组的定义,以免发生混淆。如:
• 严蔚敏《数据结构》将模式串下标从1开始计数,故定义next[1]=0,next[2]=1;
• 李春葆《数据结构》将模式串下标从0开始计数,故定义next[0]=-1,next[1]=0。
情况一: 模式串下标从1开始时求next数组的算法
若在KMP算法设计中,将模式串下标从1开始计数,则定义next[1]=0,next[2]=1。那么求next数组的算法步骤为: (1)若第j-1位的字符与第x位的字符相等,则next[j]=x+1; (2)若直到第1位依然没有字符与第j-1位的字符相等,则next[j]=1。
显然,若按严蔚敏《数据结构》中模式串的定义方式(即定义next[1]=0,next[2]=1),可得出模式串ababaaab的next数组如下:
-------------------------------------------------------
j 1 2 3 4 5 6 7 8
-------------------------------------------------------
a b a b a a a b
-------------------------------------------------------
next[j] 0 1 1 2 3 4 2 2
-------------------------------------------------------
情况二:模式串下标从0开始时求next数组的算法
若在KMP算法设计中,将模式串下标从0开始计数,则定义next[0]=-1,next[1]=0。那么求next数组的算法步骤为: (1)若第j-1位的字符与第x位的字符相等,则next[j]=x+1; (2)若直到第0位依然没有字符与第j-1位的字符相等,则next[j]=0。
显然,若按李春葆《数据结构》中模式串的定义方式(即定义next[0]=-1,next[1]=0),可得出模式串abcabaa的next数组如下:
-------------------------------------------------
j 0 1 2 3 4 5 6
-------------------------------------------------
a b c a b a a
-------------------------------------------------
next[j] -1 0 0 0 1 2 1
-------------------------------------------------
但这两种定义方式,不影响它们有一致的计算方法,即“若第j-1位的字符与第x位的字符相等,则next[j]=x+1”(特别注意:在此判别过程中,所谓的第x位是由已经计算出的next[j-1] → next[0]间的若干值跳转抵达)。
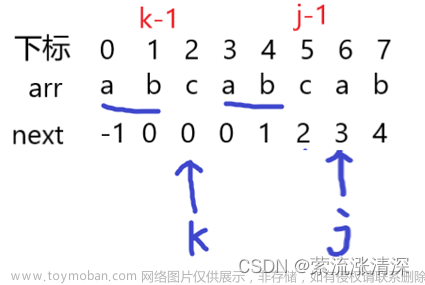
个人喜欢采用李春葆《数据结构》中模式串的定义方式(即定义next[0]=-1,next[1]=0),并据此给出了如下图所示的求j=4时模式串元素b的next数组值的图例。

【研究生考试2015年第8题】
已知字符串s为“abaabaabacacaabaabcc”,模式串t为“abaabc”。采用KMP算法进行匹配,第一次出现“失配”( s[i]!=t[j] )时,i=j=5,则下次开始匹配时,i和j的值分别是( C )。
A. i=1,j=0 B. i=5,j=0 C. i=5,j=2 D. i=6,j=2
【输出李春葆定义法next数组值的算法代码】
#include<iostream>
using namespace std;
const int maxn=100;
int ne[maxn];
void getNext(string s) {
int len=s.length(); //First of all, you must calculate the length of the string.
int i=0, j=-1;
ne[0]=-1;
while(i<len) {
if(j==-1 || s[i]==s[j]) {
ne[++i]=++j;
} else j=ne[j];
}
}
int main() {
string T;
getline(cin,T);
getNext(T);
for(int i=0; i<T.length(); i++) {
cout<<ne[i]<<" ";
}
return 0;
}
/*
input: ababaaababaa
output: -1 0 0 1 2 3 1 1 2 3 4 5
*/
【输出严蔚敏定义法next数组值的算法代码】
#include<iostream>
using namespace std;
const int maxn=100;
int ne[maxn];
void getNext(string s) {
int len=s.length(); //First of all, you must calculate the length of the string.
int i=0, j=-1;
ne[0]=-1;
while(i<len) {
if(j==-1 || s[i]==s[j]) {
ne[++i]=++j;
} else j=ne[j];
}
}
int main() {
string T;
getline(cin,T);
getNext(T);
for(int i=0; i<T.length(); i++) {
cout<<ne[i]+1<<" ";
}
return 0;
}
/*
input: ababaaababaa
output: 0 1 1 2 3 4 2 2 3 4 5 6
*/
文章来源:https://www.toymoban.com/news/detail-588397.html
【参考文献】
https://blog.csdn.net/dark_cy/article/details/88698736
https://www.zhihu.com/question/21923021
文章来源地址https://www.toymoban.com/news/detail-588397.html
到了这里,关于KMP算法 → 计算next数组的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!