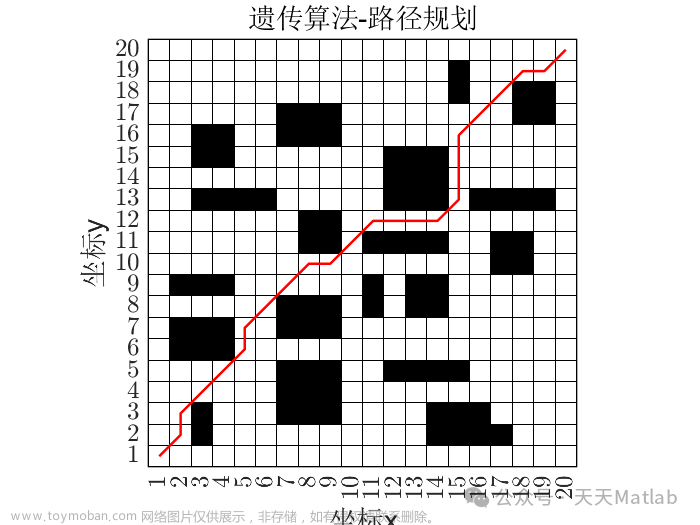
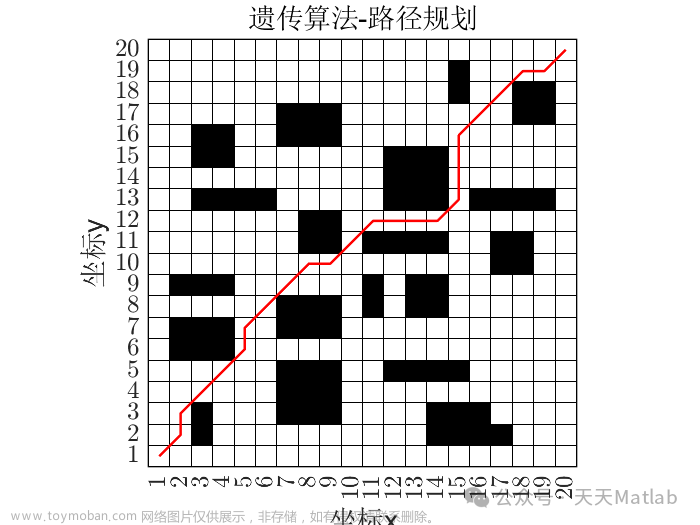
8.Roadmap路线图
即将学习的第一组离散化方法被称为路线图,该方法使用一个简单的连通图来表示配置空间——类似于用地铁地图来表示城市。

路线图方法通常分两个阶段实现:
—构建阶段从空间的连续表示中构建图形。这个阶段通常会花费大量的时间和精力,但是生成的图可以用于多个查询,只需要进行最小的修改。
—查询阶段评估图像以找到从开始位置到目标位置的路径。这是通过搜索算法来完成的。
在这个离散化部分,我们只讨论和评估每个路线图方法的构建阶段。而查询阶段将在离散化部分之后的图搜索部分中更详细地讨论。
接下来将学习的两个路线图方法是可视性(Visibility)图和Voronoi图方法。
9.可视性(Visibility)图
可视性图通过将开始节点、所有障碍物的顶点和目标节点相互连接(除了那些会导致与障碍物碰撞的节点)来构建路线图。可视性图之所以叫这个名字是有原因的——它将每个节点连接到从其位置“可见”的所有其他节点。
—节点:起点、目标和所有障碍顶点。
—边:两个节点之间不与障碍物相交的边,包括障碍物边。
下图显示了包含多边形障碍物的配置空间的可见性图。

构建可视性图的动机是,从开始节点到目标节点的最短路径将是一条分段线性路径,只在障碍物的顶点处弯曲。这在直觉上是有道理的——路径应该尽可能地贴近障碍物的边角,而不增加任何额外的长度。
一旦构建了可视性图,就可以应用搜索算法找到从起点到目标的最短路径。下图显示了可见性图中的最短路径。

小测试:
虽然用于搜索路线图的算法还没有引入,但是否有任何算法能够找到从开始到目标的路径,以及最优路径是否在路线图内,仍然值得分析。

完成测试后,现在应该已经看到了可见性图方法的优点。可见性图的一个缺点是它没有为错误留有余地。穿越最佳路径的机器人必须非常接近障碍物,这大大增加了碰撞的风险。在某些应用程序中,例如动画或视频游戏的路径规划,这是可以接受的。然而,现实世界机器人定位的不确定性使得该方法不切实际。
10.Voronoi(泰森多边形法)图
另一种生成路线图的离散化方法称为Voronoi图,与生成最短路径的可见性图方法不同,Voronoi图最大限度地提高了障碍物之间的间隙。Voronoi图是一种边缘平分障碍物之间自由空间的图。每条边都与周围的障碍物保持等距离——尽可能留出最大的间隙。如下图所示为配置空间的Voronoi图:


11.单元分解法
另一种可用于将配置空间转换为搜索算法可轻松探索的表示的离散化方法是单元分解法。单元格分解将空间划分为离散的单元格,每个单元格是一个节点,相邻单元格用边连接。有两种不同类型的单元分解:
-
精确单元格分解
- 近似单元格分解
精确单元格分解
精确单元格分解将空间划分为不重叠的网格。这通常是通过将空间分割成三角形和梯形来实现的,这可以通过在每个障碍物的顶点添加垂直线段来实现。在下面的图像中看到配置空间的精确单元格分解的结果:

一旦空间被分解,得到的图就可以用来搜索从起点到目标的最短路径。结果图如下图所示:

精确的单元格分解因为其精确性和完整性而显得优雅。每个单元要么是“满的”,意味着它完全被障碍物占据,要么是“空的”,意味着它是自由的。所有单元的并集恰好代表了配置空间。如果存在从起点到终点的路径,结果图将包含它。
为了实现精确的单元分解,算法必须沿x轴对所有障碍顶点进行排序,然后对每个顶点确定是否必须创建一个新单元,或者是否应该将两个单元合并在一起。这种算法称为平面扫描算法。
精确的单元格分解导致单元格形状怪异。形状独特的梯形和三角形的集合比规则的矩形网格更难处理。这导致了计算复杂度的增加,特别是对于具有较多维度的环境。当障碍物不是多边形而是不规则形状时,分解计算也很困难。
由于这个原因,存在另一种类型的单元格分解,它在实现中更加实用。
12.近似单元格分解
近似单元格分解将配置空间划分为简单、规则形状的离散单元格——例如矩形和正方形(或它们的多维等量物)。除了简化单元格的计算外,该方法还支持空间的层次分解(下面将详细介绍)。
简单的分解
二维配置空间可以分解为矩形单元格的网格。然后,每个单元格可以像之前一样标记为满或空。然后,搜索算法可以寻找一个空闲单元格序列来连接开始节点和目标节点。
这种方法比精确的细胞分解更有效,但失去了完整性。一个特定的配置空间可能包含一个可行路径,但是由于存在障碍物,单元格的分辨率导致一些包含路径的单元格被标记为“满”。不管单元格中99%的空间被障碍物占据,还是只有1%的空间被障碍物占据,它都会被标记为“满”。显然,这是不实在的。
迭代分解
还有一种将空间划分为简单单元格的方法。该方法不是立即将空间分解为大小相等的小单元,而是递归地将空间分解为四个象限。每个象限被标记为满、空或一个名为“混合”的新标签——用于表示一些被障碍物占据,但也包含一些空闲空间的单元格。如果从头到尾找不到一个空闲空间的单元,那么混合单元将进一步分解为另外四个象限。通过这个过程,更多的空闲单元将出现,最终揭示出一条路径(如果存在的话)。这种方法的二维实现称为四叉树分解。可以在下面的图表中看到:

算法
近似单元格分解背后的算法比精确单元格分解算法简单得多。下面提供了该算法的伪代码:


四叉树的三维等效物是八叉树,如下图所示。离散具有任意维数的空间的方法遵循与上面描述的算法相同的过程,但是扩展以适应额外的维数。

尽管精确的单元格分解是一种更优雅的方法,但对于非普通环境,它比近似的单元格分解计算成本要高得多。因此,在实践中通常采用近似的单元分解方法。经过足够的计算,近似的单元格分解接近完整。然而,这并不是最优的——最终的路径取决于单元格如何分解。
近似的单元格分解可以快速找到明显的解决方案。最优路径有可能挤过障碍物之间的一个极小的开口,但最终路径在广阔的开放空间中需要更长的路线——这是递归分解算法首先找到的。近似的单元分解是功能性的,但是像所有离散/组合路径规划方法一样,它开始在高维环境中难以计算。

13.势场Potential Field
本文要学习的最后一种离散化方法——势场法。与迄今为止讨论的将连续空间离散成连通图的方法不同,势场方法执行不同类型的离散化。
为了完成它的任务,势场法生成了两个函数——一个将机器人吸引到目标,另一个将机器人驱逐开障碍物。这两个函数可以相加以创建离散化表示。通过应用梯度下降等优化算法,机器人可以在绕过障碍物的同时向目标空间移动。让我们更详细地看看这些步骤是如何实现的。
吸引势场
吸引势场是在目标配置下具有全局最小值的函数。如果一个机器人被放置在任意一点,并被要求沿着下降最陡的方向,它将最终达到目标配置。这个函数不需要很复杂,一个简单的二次函数就可以实现上面讨论的所有要求。

排斥势场
排斥势场在自由空间中是一个等于零的函数,在障碍物附近增长到一个较大的值。创建这样一个势场的一种方法是使用下面的函数。

值ρ0控制势场离障碍物的非零距离,以及障碍物周围的区域有多陡。超过ρ0时,势场为0。在距离障碍物的ρ0范围内,势场随距离障碍物的远近而成比例。
势场和
将吸引函数和排斥函数相加,得到用于引导机器人从空间中的任何地方到达目标的势场。下图显示了函数的和,紧接着的图像显示了最终函数。


想象一下,在函数的表面上放置一个弹珠——它将从场上的任何地方朝目标的方向滚动,而不会与任何障碍物碰撞(只要ρ0设置得当)!
函数的梯度决定了机器人应该移动的方向,速度可以设置为常数,或者根据机器人和目标之间的距离缩放。
势场法的问题
势场法并非没有缺点,它既不完整也不最优。在某些环境下,该方法将引导机器人到达局部最小值,而不是全局最小值。下面的图片描述了这样一个例子。根据机器人从哪里开始,它可能会被引导到微笑图的底部。下图描述了配置空间,后面图显示了对应的势场。


机器人陷入局部最小值的问题可以通过添加随机行走和其他通常应用于梯度下降的策略来解决,但最终该方法并不完整。
势场法也不是最优的,因为它可能并不总是找到从起点到目标的最短(或最便宜)路径。最短的路不一定是最陡峭的下坡路。此外,势场没有考虑每一步的代价。
本文总结如下图示:

文章来源地址https://www.toymoban.com/news/detail-589053.html
文章来源:https://www.toymoban.com/news/detail-589053.html
到了这里,关于机器人学习-关于经典路径规划(二)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!