学堂在线数据结构(上)(2023春)邓俊辉 课后作业错题整理

CTRL+F可进行页面搜索~૮꒰ ˶• ༝ •˶꒱ა

1. The reverse number of a sequence is defined as the total number of reversed pairs in the sequence, and the total number of element comparisons performed by the insertion sort in the list of size n is:
   一个序列的逆序数定义为该序列中的逆序对总数，规模为n的列表中插入排序进行的元素比较总次数为:
   
   1答案：B

2. For ordered subsequences (set their length to k) during insertion sorting.
   对于插入排序过程中的已排序子序列（设其长度为k）：
   
   2答案：C

3. If in the recursive version of pre-order traversal, the access to the root node is followed by accessing the right subtree first and then the left subtree, then the call stack order of the left and right subtrees is:
   若在递归版先序遍历中规定访问完根节点后先访问右子树再访问左子树，则左、右子树的调用栈顺序是：
   
   3答案：A

4. 在一棵树中,顶点p是顶点v的父亲,则它们的高度的关系是
   
   4答案：A

5. Read the function below (where 1≤x, y≤16) and indicate its function:
   阅读下面函数(其中1≤x, y≤16)，指出其功能：
   
   
   5答案：A
解析：This function is a recursive version of the conversion of number systems
该函数是进制转换的递归版。

6. which of the following are equal
   ① Numbers of different n-bit binary
   ② The number of legal parentheses matched by n pairs of parenthesesn
   ③ Numbers of different stack shuffle for {1, 2 … n}
   ④ Number of operator stack push operations during infix expression evaluation with n operators
   以下几个量中相等的是:
   ①不同的n位二进制数个数
   ②对小括号所能构成的合法括号匹配个数
   ③{1, 2 … n}的不同栈混洗个数
   ④含n个运算符的中缀表达式求值过程中运算符栈push操作的次数
   6答案：②③
解析：The push and pop in the stack shuffle correspond to the "(" and ")" in the parentheses match, so they are equal in number. (1 is 2^n, 2 is Catalan(n), 3 is Catalan(n), 4 ≤n)
栈混洗中的push和pop分别对应于括号匹配中的”( ”和”) ”,故它们数量相等.(①为2^n,②为 Catalan(n),③ 为Catalan(n),④≤n)

7. The graph G contains n vertices (n>0), implemented with an adjacency matrix. How many items have been added to the adjacency matrix after adding a new vertex?
   图G包含n个顶点(n>0)，用邻接矩阵实现。在其中加入一个新的顶点后邻接矩阵增加了多少项？
   
   7答案：D
Adjacency matrix adds one row and one column 邻接矩阵增加了一行一列

8. Which of the following options is correct:
   下列说法中正确的是：
   
   8C

9. Is it possible to replace:
   for (int i = 0; i < _size; i++) _elem[i] = oldElem[i];
   in the vector expansion code in the video with:
   memcpy(_elem, oldElem, _size * sizeof(T));
   P.S.This question involves the relevant knowledge of C++
   是否可以将视频里向量扩容代码中的：for (int i = 0; i < _size; i++) _elem[i] = oldElem[i];替代为：memcpy(_elem, oldElem, _size * sizeof(T));P.S.本题涉及C++的相关知识
   
   9.D
解析：When T is a non-base type and there is a corresponding assignment operator to perform deep copy, the previous section of code calls the assignment operator, and the latter section can only perform shallow copy.
当T为非基本类型且有对应的赋值运算符以执行深复制时，前一段代码会调用赋值运算符，而后一段只能进行浅复制。

10. Using the expansion strategy of appending fixed memory space each time, the amortized time complexity of inserting element of vector of size n is:
    采用每次追加固定内存空间的扩容策略，规模为n的向量插入元素的分摊时间复杂度为：
    10答案O(n)

11. For a vector of size n, the optimal time complexity for binary search versions A and B is:
    对于规模为n的向量，二分查找版本A和B的最优时间复杂度分别为：
    
    11D
解析：The best case of version A is hitting at the first time, only Θ(1)
版本A的最优情况即第一次就命中，只需Θ(1)的时间

12. For binary search version C, what is the next search range when e<V[mi] is not established: 对于二分查找版本C，当e<V[mi]不成立时下一步的查找范围是：
    
    12.D

13. For binary search version C, when the length of the search interval is reduced to 0, V[lo] is: 对于二分查找版本C，当查找区间的长度缩小为0时，V[lo]是：
    
    13C
[nianjin原创解析]考察不变性。 不变性说的是，当lo == hi，A[lo]总是大于e的最左者。不变性的证明是通过归纳法证明的。考虑0~lo区间和hi~n区间由空集开始的扩张。第一种情况，如果e<A[mi]，hi~n扩张到mi+1~n，因为A[mi]>e 所以A[mi+1]>e，扩张是满足不变性的。另一种情况，A[mi]<=e，0~lo扩张到0~mi，因为A[mi]<=e，所以A[mi-1]<=e，扩张也是满足不变性的。证明完毕。该题B和C的区别在于，B描述的是A[lo-1]
    扩：版本C的二分查找返回的是A[lo-1]，插入的位置是后一个

14. Which of the following is NOT a component of a Turing machine? 以下哪项不是图灵机的组成要件？
    A. A tape of finite length 有限长的纸带
    B. A finite alphabet 有限的字母表
    C. A finite set of states 有限种状态
    D. A head for reading and writing 读写头
    A 无限长纸袋

15. True of false: The RAM model is equipped with a finite amount of storage, which differs from the Turing machine. 判断正误：RAM模型与图灵机模型的区别在于图灵机的存储空间无限，而RAM的存储空间有限。
    错
解析The RAM model poses no limitation on the number of registers (which is never the case for a real computer), making it equivalent to the Turing machine.
RAM模型中寄存器的总数没有限制（虽然我们平时使用的计算机无法做到），它与图灵机是等价的。

16. Which of the following equations is wrong? 下列对应关系中错误的是
    
    D logn

17. True or false: To apply decrease-and-conquer, we divide the original problem into two degenerated sub-problems, solve them, and merge their solutions. 判断：减而治之的思想是：将问题划分为两个平凡的子问题，分别求解子问题，来得到原问题的解。
    错
解析Rather than "divide the original problem into two degenerated sub-problems", we divide it into a degenerated sub-problem and a sub-problem with reduced size.We refer to a problem as "degenerated" when its solution is directly available. For example, sorting n numbers is a complex problem, but it becomes degenerated when n == 1, in which case we don't have to do anything.
“划分为两个平凡的子问题”这一描述有误，应当是划分为一个平凡、一个规模缩减的两个子问题。 所谓“平凡的问题”，是指无需进行复杂运算，可以直接给出结果的问题。例如，“对n个数进行排序”是一个复杂的问题，但当n等于1时，问题便成为了一个平凡的问题，因为序列长度为1，则序列自然是有序的。
    扩：“递归基”是递归函数的一种平凡情况，只有有递归基，递归才不会一直进行下去。
    扩2：减而治之的算法中，递归实例分别是：1个规模为n的实例、1个规模为n-1的实例、1个规模为n-2的实例、…，共有n个。分而治之的算法中，递归实例分别是：1个规模为n的实例、2个规模为n/2的实例、4个规模为n/4的实例、…，共有1+2+4+8+…+n个。

18. For the staircase problem in the video lecture, how many different ways can get you from the first step to the eighth. 对于视频中的上台阶问题（从第一层开始），上到第8层共有多少种不同的走法
    f8 = 21

19 bigO记号

O(1)<O(log n)<O(n^c)<O(aⁿ)

20. Why the suffix of the deleted element is moved from front to back in the interval deletion algorithm remove(lo, hi)?
    为什么区间删除算法remove(lo, hi)中要从前向后移动被删除元素的后缀？

B

21. Why doesn’t the algorithm need to call remove() to delete an element?
    为什么该算法中不需要调用remove()进行元素删除？

21 B

22. The repeating elements in the ordered vector must be adjacent, and the algorithm ignores duplicate elements between different elements. 有序向量中重复元素必然紧邻，而算法中忽略了互异元素间的重复元素
    V={2, 3, 5, 7, 11, 13, 17}. How many comparisons V.search(16, 0, 7) need to make? V={2, 3, 5, 7, 11, 13, 17}。V.search(16, 0, 7)需要进行多少次比较？
    5次

23. Insert the element e in the ordered vector V and keep it in order, which of the following code is correct: 在有序向量V中插入元素e并使之保持有序，下列代码正确的是:
    
    D

24. Which of the following functions grows fastest asymptotically?
    下列函数渐进增长速度最快的是：
    
    B C<D<A<B

25. For vectors of size n, the optimal and worst-case time complexity for merge sorting is: 对于规模为n的向量，归并排序的最优、最坏时间复杂度分别为：

什么是最优时间复杂度

B

26. The binary search for “version C” is extracted as follows:二分查找“版本C”摘录如下：
    The vector V={2, 3, 5, 7, 11, 13, 17, 19} is used to find the target element 16 in V. The elements that have been compared with the target element in the whole process are:向量V={2, 3, 5, 7, 11, 13, 17, 19}，在V中使用它查找目标元素16，整个过程中与目标元素发生过比较的元素依次为：
    
    
    26.A

27. The following function is a recursive version of the binary search:以下函数是二分查找的递归版：
    For a vector of size n, the time and space complexity of the recursive version and the iterated version learned in class are: 对于规模为n的向量，该递归版的时间、空间复杂度和课堂上所学的迭代版的时间、空间复杂度分别是：
    
    
    27. D
    The Implementation process of the recursive version is similar to the iterative version, with the same time complexity, but the space complexity of the recursive version is equal to the maximum recursion depth, which is Θ(〖log〗_2 n), and the iteration version uses only constant unit aids space. 该递归版与迭代版执行流程相似，时间复杂度相同，但是递归版的空间复杂度等于最大递归深度，在此处即Θ(〖log〗_2 n)，而迭代版只用了常数单位的辅助空间。

28. 如果把朋友圈视为一无向图，那么即使A君看不到你给B点的赞，你们仍可能属于同一双连通分量。
    对 考虑：ACBY，形成一个环。Y(You)代表你自己。

29. Searching for search elements 7 with interpolation in the vector V={2, 3, 5, 7, 11, 13, 17, 19, 23}
    在向量V={2, 3, 5, 7, 11, 13, 17, 19, 23}中用插值查找搜索元素7
    Guess the pivot point mi=?
    猜测的轴点mi=?
    1

30. How many nodes could be in complete binary tree of height h?
    高度为 h 的完全二叉树可能有多少个节点?
    
    B
解析：一颗高度为h的完全二叉树，其节点的取值范围为：[2^h, 2^(h+1)-1]。 请注意：一个节点的高度（height）是指从该节点到最深的叶子的边（edges）的数量。 例如，根据定义，具有 h 条边和 h+1 个节点的路径，其高度（height）为 h 而不是 h+1。又如，具有单个节点（根）的二叉树的长度为 0；具有 4 个节点的完全二叉树的高度为 2。

31. In order to traverse the binary tree, the successor of the node v in the order traversal is (assuming that the successor of v exists):对二叉树进行中序遍历，节点v在中序遍历下的后继为（假设v的后继存在）：
    
    C
When v does not have a right subtree, its successor is an ancestor, specifically the ancestor that first turned right along the parent pointer.
当v没有右子树时它的后继为某个祖先，具体地说是在沿着parent指针向上的过程中第一次向右的祖先。

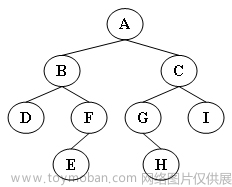
32. Similar to pre-order and in-order traversal, accessing the binary tree in the order of left child->right child->root node is called post-order traversal. The first visited node in the post-order traversal is与先序、中序遍历类似，以左子->右子->根节点的顺序来访问二叉树称为后序遍历。后序遍历中第一个被访问的节点是：
    
    D
解析： Starting from the root node, for each node in the middle, you can go left to the left and not to the left. If there is no way to go, then the node is the first node to be visited in the subsequent traversal.从根节点开始，对于中途每个节点，能往左就往左，不能往左就往右，若左右都无路可走，则该节点是后序遍历中第一个被访问的节点。

33. G is a directed acyclic graph, and (u, v) is an edge in G that points from u to v. The result of DFS on G is: G是有向无环图，(u, v)是G中的一条由u指向v的边。对G进行DFS的结果是：
    
    C
G does not contain a loop, (u, v) cannot be BACKWARD, and access to v must have ended when access to u ends G不含环路，(u, v)不可能是BACKWARD，对u的访问结束时对v的访问必然已经结束

34. G is a simple undigraph, A is an adjacency matrix of G, M is an associative matrix of G, and D is a diagonal matrix of the degree of the i-th element of the vertex on the diagonal. Their relationship is: G是简单无向图，A为G的邻接矩阵，M为G的关联矩阵，D是对角线上第i个元素为顶点i的度的对角矩阵,它们的关系是：
    
    B
Use the example to verify, or see the analysis of the textbook matching exercises 6-1 用例子验证，或见教材配套习题解析6-1文章来源地址https://www.toymoban.com/news/detail-589166.html

到了这里，关于学堂在线数据结构(上)(2023春)邓俊辉 课后作业错题整理的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！