机器学习笔记之高斯网络(二)高斯贝叶斯网络-Toy模板网

这篇具有很好参考价值的文章主要介绍了机器学习笔记之高斯网络(二)高斯贝叶斯网络。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

引言

上一节介绍了高斯网络及其条件独立性，本节将介绍高斯贝叶斯网络。

回顾

高斯网络

高斯网络最核心的特点是：随机变量集合中的随机变量均是连续型随机变量，并且均服从高斯分布：
已知某随机变量集合 $\mathcal X$ 中包含 $p$ 个特征，整个高斯网络中所有结点的联合概率分布服从多元高斯分布：
$\begin{aligned} \mathcal X & = (x_1,x_2,\cdots,x_p)^T \\ \mathcal P(\mathcal X) & = \frac{1}{(2\pi)^{\frac{p}{2}}|\Sigma|^{\frac{1}{2}}} \exp \left[-\frac{1}{2}(x - \mu)^T\Sigma^{-1}(x - \mu)\right] \end{aligned}$
其中期望 $\mu$ ，协方差矩阵 $\Sigma$ 表示如下：
$\mu = \begin{pmatrix} \mu_1\\ \mu_2 \\ \vdots \\ \mu_p \end{pmatrix}_{p \times 1} \quad \sigma = \begin{pmatrix} \sigma_{11},\sigma_{12},\cdots,\sigma_{1p} \\ \sigma_{21},\sigma_{22},\cdots,\sigma_{2p} \\ \vdots \\ \sigma_{p1},\sigma_{p2},\cdots,\sigma_{pp} \\ \end{pmatrix}_{p \times p}$

随机变量之间的边缘独立性：如果随机变量 $x_i,x_j (i,j \in \{1,2,\cdots,p\};i\neq j)$ 对应协方差矩阵的结果 $Cov(x_i,x_j) = \sigma_{ij} = 0$ ，那么称 $x_i,x_j$ 是不相关的。也称 $x_i,x_j$ 边缘独立或者绝对独立：
$\sigma_{ij} = 0 \Rightarrow x_i \perp x_j$
随机变量之间的条件独立性：如果随机变量 $x_i,x_j(i,j \in \{1,2,\cdots,p\};i \neq j)$ 对应精度矩阵(Precision Matrix)结果 $\lambda_{ij} = 0$ ,称给定除去 $x_i,x_j$ 之外其他结点的条件下， $x_i,x_j$ 相互独立：
其中 $\Lambda = [\lambda_{ij}]_{p \times p}$ 表示精度矩阵，它是协方差矩阵的‘逆矩阵’。
$\lambda_{ij} = 0 \Rightarrow x_i \perp x_j \mid x_{-i-j}$

贝叶斯网络：因子分解

基于贝叶斯网络有向图的性质，针对随机变量集合 $\mathcal X$ 的联合概率分布 $\mathcal P(\mathcal X)$ 进行表达。
已知随机变量集合 $\mathcal X$ 包含 $p$ 个维度特征，因而 $\mathcal X$ 的联合概率分布 $\mathcal P(\mathcal X)$ 表示如下：
$\mathcal P(\mathcal X) = \mathcal P(x_1,x_2,\cdots,x_p)$
针对联合概率分布求解，最朴素的方式是条件概率的链式法则(Chain Rule)：
$\mathcal P(x_1,x_2,\cdots,x_p) = \mathcal P(x_1) \cdot \prod_{i=2}^p \mathcal P(x_i \mid x_1,\cdots,x_{i-1})$
但如果随机变量集合 $\mathcal X$ 维度过高，这种链式法则计算代价很大。可以将对应的概率图模型视作完全图——任意两个特征之间都需要求解其关联关系。
而贝叶斯网络的条件独立性 可以极大程度地简化运算过程。给定贝叶斯网络的表达方式，可以直接写出各节点的联合概率分布：
$\mathcal P(x_1,x_2,\cdots,x_p) = \prod_{i=1}^p \mathcal P(x_i \mid x_{pa(i)})$
其中 $x_{pa(i)}$ 表示 $x_i$ 结点的父节点组成的集合。

高斯贝叶斯网络：因子分解

已知贝叶斯网络中一共包含 $p$ 个结点，它的联合概率分布(因子分解)表示如下：
$\mathcal P(\mathcal X) = \prod_{i=1}^p \mathcal P(x_i \mid x_{pa(i)})$

从 全局模型(Global Model) 角度观察，高斯贝叶斯网络是基于线性高斯模型(局部模型(Local Model))的模型架构。

局部模型架构：对于线性高斯模型并不陌生，在卡尔曼滤波中对线性高斯模型又了一定认识。

从宏观角度认识线性高斯模型，即模型中某节点与父结点之间存在线性关系，并且噪声服从高斯分布：
可以理解为：高斯贝叶斯网络中的‘有向边’表示节点与父节点之间的‘具有高斯分布噪声的线性关系’。
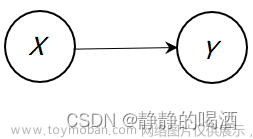
这里已知 $\mathcal X,\mathcal Y$ 是两个随机变量集合， $\mathcal X$ 的边缘概率分布 $\mathcal P(\mathcal X)$ 和条件概率分布 $\mathcal P(\mathcal Y \mid \mathcal X)$ 表示如下：
$\begin{cases} \mathcal P(\mathcal X) \sim \mathcal N(\mu_{\mathcal X},\Sigma_{\mathcal X}) \\ \mathcal P(\mathcal Y \mid \mathcal X) \sim \mathcal N(\mathcal A \mathcal X + \mathcal B,\Sigma_{\mathcal Y}) \end{cases}$
局部模型描述结点之间的关联关系 表示如下：

同理，关于结点 $\mathcal Y$ 的边缘概率分布 $\mathcal P(\mathcal Y)$ 以及 $\mathcal P(\mathcal X),\mathcal P(\mathcal Y \mid \mathcal X)$ 的推断结果 $\mathcal P(\mathcal X \mid \mathcal Y)$ 同样服从高斯分布。具体结果表示如下：
推导过程详见：高斯分布——推断任务之边缘概率分布与条件概率分布
$\begin{aligned} \mathcal P(\mathcal Y) & \sim \mathcal N(\mathcal A \mu + \mathcal B,\mathcal A\Sigma_{\mathcal X}\mathcal A^T + \Sigma_{\mathcal Y}) \\ \mathcal P(\mathcal X \mid \mathcal Y) & \sim \mathcal N(\Sigma\left\{\mathcal A^T\Sigma_{\mathcal Y}^{-1}(\mathcal Y - \mathcal B) + \mathcal A \mu\right\},\Sigma) \quad \Sigma = \Sigma_{\mathcal X}^{-1} + \mathcal A^T \Sigma_{\mathcal Y}^{-1}\mathcal A^{-1} \end{aligned}$

实际上，卡尔曼滤波(Kalman Filter)自身就是一个特殊的高斯贝叶斯网络。它的概率图模型表示如下：
高斯贝叶斯网络,机器学习,概率论,高斯贝叶斯网络,因子分解
由于齐次马尔可夫假设、观测独立性假设的约束，概率图中无论是观测变量 $\mathcal O = \{o_1,\cdots,o_T\}$ 还是隐变量 $\mathcal I = \{i_1,\cdots,i_T\}$ ，它们均仅有一个父节点：

基于齐次马尔可夫假设，相邻隐变量 $i_t,i_{t-1}$ 之间的条件概率表示为：
$\mathcal P(i_t \mid i_{t-1}) \sim \mathcal N(\mathcal A \cdot i_{t-1} + \mathcal B,\mathcal Q)$
基于观测独立性假设，隐变量 $i_t$ 与对应时刻观测变量 $o_t$ 之间的条件概率表示为：
$\mathcal P(o_t \mid i_t) \sim \mathcal N(\mathcal C\cdot {i_t} + \mathcal D,\mathcal R)$

基于上述假设，对随机变量之间关联关系的表示(Representation)描述为：
之所以将噪声均值设置为0 -> 均值偏差可以归纳到对应偏置项 $\mathcal B,\mathcal D$ 中。
$\begin{cases} i_t = \mathcal A \cdot i_{t-1} + \mathcal B + \epsilon \quad \epsilon \sim \mathcal N(0,\mathcal Q) \\ o_t = \mathcal C \cdot i_t + \mathcal D + \delta \quad \delta \sim \mathcal N(0,\mathcal R) \end{cases}$

相比之下，高斯贝叶斯网络并没有假设约束，结点中可能存在多个父节点组成的集合。
给定一个高斯贝叶斯网络的局部图如下：
这里仅讨论 $x_i$ 与其父节点们之间的关系，其余部分略掉了。
高斯贝叶斯网络,机器学习,概率论,高斯贝叶斯网络,因子分解
很明显： $x_1,x_2,\cdots,x_k$ 均是 $x_i$ 的父节点，将局部模型延伸到一个更大的局部模型。
这里 $x_1,x_2,\cdots,x_k$ 以及 $x_i$ 均是一维随机变量：

假设 $x_i$ 的父节点集合中仅包含一个随机变量( $x_1$ 为例)，那么 $\mathcal P(x_{i} \mid x_{pa(i)})$ 可表示为：
- 这里定义的 $\mu_i,\sigma_i^2$ 是表示 $x_1,x_i$ 之间线性关系中噪声的高斯分布，但是高斯贝叶斯网络中定义的噪声 $\epsilon\sim \mathcal N(0,\sigma_i^2)$ ,因而相当于 $\mu_i$ 单独被提出来，因为 $\mu_i$ 就是表示关于分布的‘位置信息’。因此，下面公式中的 $\epsilon$ 才是真正噪声的分布形态。
- 因而参数 $\mu_i$ 是自然存在的。文章参考：概率密度函数角度认识最小二乘法
  $\begin{aligned} x_i & = w_{i1} \cdot x_1 + \epsilon \quad \epsilon \sim \mathcal N(\mu_i,\sigma_i^2)\\ \mathcal P(x_{i} \mid x_{pa(i)}) & \to \mathcal P(x_i \mid x_1) \sim \mathcal N(w_{i1} \cdot x_1 + \mu_i,\sigma_{i}^2) \\ \end{aligned}$
对应 $x_i,x_1$ 随机变量之间关联关系的表示 为：
$x_i = \mu_i + w_{i1} \cdot (x_1 - \mu_1) + \sigma_{i}\cdot \epsilon_i \quad \epsilon \sim_i \mathcal N(0,1)$
关于上述公式的一些个人理解：
- 多出来的 $\mu_1$ 是哪来的：
  为了简化运算，通常对‘随机变量的分布’进行平移’，就是去中心化。
- 执行线性运算之后，方差必然会发生变化。应变化为 $w_{i1}^2 \cdot \sigma_i^2$ ,但是 $\mathcal P(x_i \mid x_1)$ 并没有变化,依旧是 $\sigma_i^2$ ：方差变化是 $x_i$ 的边缘概率分布 $\mathcal P(x_i)$ ,而不是 $\mathcal P(x_i \mid x_1)$ ,这也是线性高斯模型的假设方式。
- 偏置项去哪了：最终都需要‘去中心化’，将分布的均值(中心)回归零点，因而被省略掉了，或者也可理解为‘合并到’ $\mu_i$ 中。
欢迎小伙伴们交流讨论。
同理，父结点集合中包含多个随机变量，将父结点集合看成向量形式，因而 $x_{pa(i)}$ 以及对应权重信息 $\mathcal W_i$ 表示如下：
$\begin{aligned} x_{pa(i)} = (x_1,x_2,\cdots,x_k)_{k \times 1}^T \\ \mathcal W_i = (w_{i1},w_{i2},\cdots,w_{ik})_{k \times 1}^T \end{aligned}$
至此， $\mathcal P(x_i \mid x_{pa(i)})$ 表示如下：
$\begin{aligned} \mathcal P(x_i \mid x_{pa(i)}) & = \mathcal N(\mathcal W_i^T x_{pa(i)} + \mu_i,\sigma_i^2) \\ & = \mathcal N((x_1 \cdot w_{i1} + \cdots + x_k \cdot w_{ik}) + \mu_i,\sigma_i^2) \end{aligned}$
因而 $x_i,x_{pa(i)}$ 随机变量之间的关联关系表示为：
$\begin{aligned} x_i - \mu_i & = \mathcal W_i^T (x_{pa(i)} - \mu_{pa(i)}) + \sigma_i \cdot \epsilon_i \\ & = \begin{pmatrix}w_{i1},w_{i2},\cdots,w_{ik}\end{pmatrix}_{1 \times k} \left[\begin{pmatrix}x_1 \\ x_2 \\ \vdots \\ x_k \end{pmatrix} - \begin{pmatrix}\mu_1 \\ \mu_2 \\ \vdots \\ \mu_k \end{pmatrix}\right]_{k \times 1} + \sigma_i \cdot \epsilon_i\\ & = \sum_{j \in x_{pa(i)}} w_{ij}(x_j - \mu_j) + \sigma_i \cdot \epsilon_i \end{aligned}$