2022 RoboCom 世界机器人开发者大赛-本科组（省赛）-- 第五题树与二分图 (已完结)-Toy模板网

这篇具有很好参考价值的文章主要介绍了2022 RoboCom 世界机器人开发者大赛-本科组（省赛）-- 第五题树与二分图 (已完结)。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

其它题目

题目

RC-u5 树与二分图

设 G=(V,E) 是一个无向图，如果顶点集合 V 可分割为两个互不相交的子集 (A,B)，并且每条边 (i,j)∈E 的两个端点 i 和 j 分别属于这两个不同的顶点子集，则称图 G 为一个二分图。

现在给定一棵树 T，要求选择树中两个没有边相连的结点 i 和 j，使得将无向边 (i,j) 加进 T 后能够构成二分图。你的任务是计算满足这个要求的选择方案有多少种。

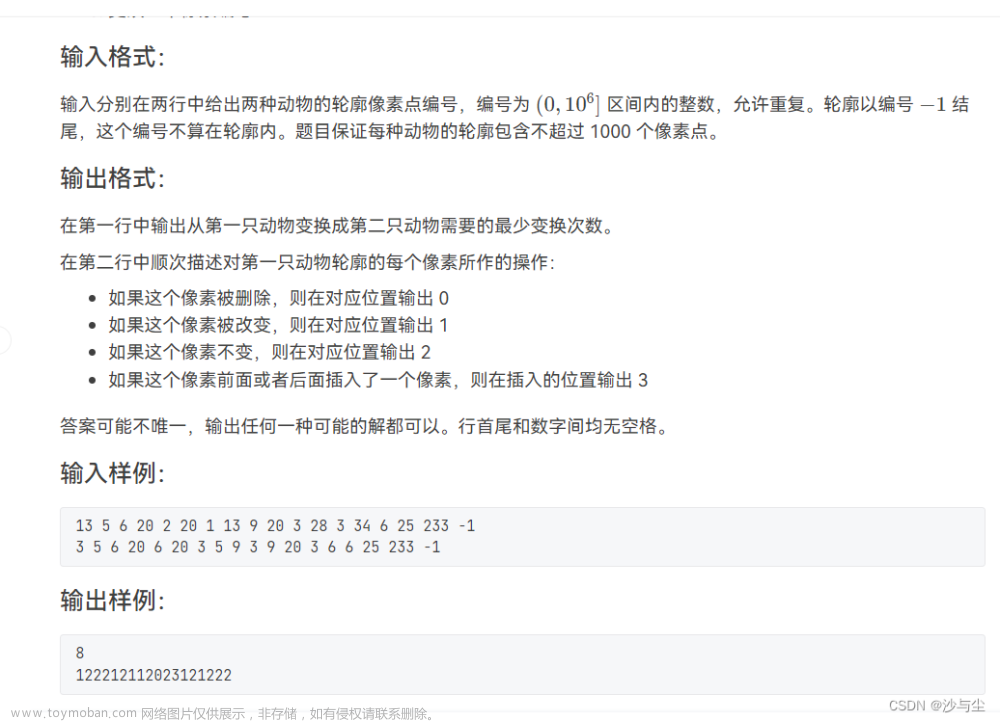
输入格式:
输入第一行给出一个正整数 N (2≤N≤1e6)，表示树中结点的个数。

接下来 N−1 行，每行给出树中一条边的两端结点编号，以空格分隔。结点编号从 1 开始。题目保证输入给出的是一棵树中所有的边。

输出格式:
在一行中输出方案数。注意：连接 (1,2) 和 (2,1) 视作同一个方案。

输入样例:
7
1 2
2 3
2 4
2 5
2 6
4 7
输出样例:
4

题解

思路分析
二分图, 简而言之，就是顶点集V可分割为两个互不相交的子集，并且图中每条边依附的两个顶点都分属于这两个互不相交的子集，两个子集内的顶点不相邻。

不难发现, 树一定是二分图. 因为树很重要的一个性质是除根结点外每个结点有且仅有一个父结点, 所以我们可以把树中的每个结点与它的父结点放到两个不同的集合中, 最后整颗树的结点集都可以划分到两个不相交集合中.

所以题意就是, 对于给定的二分图, 最多能加多少边使得它仍是二分图

对于顶点数为n的二分图, 假设划分的两个集合顶点数分别为m , n-m. 显然这个二分图的最大边数为m*(n-m), 即每个顶点与对面集合所有顶点都形成的边.

由此, 我们只需要得出任一集合数量, 就可以算出最大边数, 减去已有边数即为答案

关键点实现

在存储问题上, 虽然题目给的是一棵树, 但我们仍然要将它当成图来看待, N比较大, 所以用邻接表来存图.

int h[N], e[N], ne[N], idx;

void add(int x, int y)
{
    e[idx] = y, ne[idx] = h[x], h[x] = idx++;
}

在获取某个集合中顶点数量的问题上, 我们可以用类似染色法的技巧对图进行一次遍历.
用布尔值true/false来代表两种颜色, 只对一种颜色进行计数.
当前顶点的邻接点的颜色一定与当前顶点相反, 即在另一个集合

bool st[N];
ll m;
void dfs(int v, bool color)
{
    st[v] = true;
    if(color) m++;
    for(int i=h[v]; i!=-1; i=ne[i])
    {
        int j = e[i];
        if(!st[j]) dfs(j, !color);
    }
}

AC代码

#include <bits/stdc++.h>

using namespace std;
#define ll long long
const int N = 1e6 + 10;

ll n;
int h[N], e[N], ne[N], idx;

void add(int x, int y)
{
    e[idx] = y, ne[idx] = h[x], h[x] = idx++;
}

bool st[N];
ll m;
void dfs(int v, bool color)
{
    st[v] = true;
    if(color) m++;
    for(int i=h[v]; i!=-1; i=ne[i])
    {
        int j = e[i];
        if(!st[j]) dfs(j, !color);
    }
}

int main()
{
    cin >> n;
    for(int i=1; i<=n; i++) h[i] = -1;
    int x, y;
    for(int i=1; i<n; i++)
    {
        cin >> x >> y;
        add(x, y), add(y, x);
    }
    dfs(1, true);//从任一顶点开始遍历
    cout << m*(n-m) - (n-1);
    return 0;
}