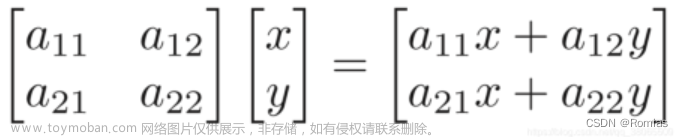说明
关于齐次变换矩阵的左乘与右乘问题,本质上是所有的变换都相对于最开始的坐标系,还是所有变换都相对于新得到的坐标系的问题。
结论
这里直接给出结论,所有的变换都相对于最开始的坐标系用左乘;所有变换都相对于新得到的坐标系用右乘。
注:如果想要深入理解,“所有的变换都相对于最开始的坐标系用左乘”可以从点的操作(point operator)去理解;“所有变换都相对于新得到的坐标系用右乘”可以从坐标系变换(coordinate transformation)去理解。文章来源:https://www.toymoban.com/news/detail-595265.html
点的操作(point operator)、坐标系变换(coordinate transformation)参见https://blog.csdn.net/jppdss/article/details/131686922文章来源地址https://www.toymoban.com/news/detail-595265.html
到了这里,关于随手笔记——关于齐次变换矩阵的左乘与右乘的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!