NP-hard问题
NP(Non-deterministic Polynomial)-hard problem
一、预备知识
1.多项式
多项式定义：就是一元
n
n
n次方式
2.时间复杂度
表明问题扩大后，程序需要的时间长度增长地有多快。
（1）多项式级的复杂度：eg.
O
(
1
)
O(1)
O(1),
O
(
l
o
g
n
)
O(log n)
O(logn),
O
(
n
a
)
O(n^a )
O(na)，时间复杂度为多项式的问题都很容易解出来.
（2）非多项式级的：eg.
O
(
a
n
)
O(a^n)
O(an),
O
(
n
!
)
O(n!)
O(n!)
3.约化
一个问题A可以约化为B的含义是，可以用问题B的解法解决问题A。
二、基础概念
问题定义：
P问题：一个问题可以在多项式
(
O
(
n
k
)
)
(O(n^k))
(O(nk))的时间复杂度内解决（简单的问题）；
例如：n个数的排序问题（不超过
O
(
n
2
)
O(n^2)
O(n2)）
NP问题： 一个问题的解可以在多项式的时间内被证实或证伪，即给出一个答案，可以很快地（在多项式时间内）验证这个答案是对的还是错的，但是不一定能在多项式时间求出正确的解；
例如： 背包客问题，任何一条路线方案都可以很快地被计算代价，但是无法在多项式时间内求出最优解。
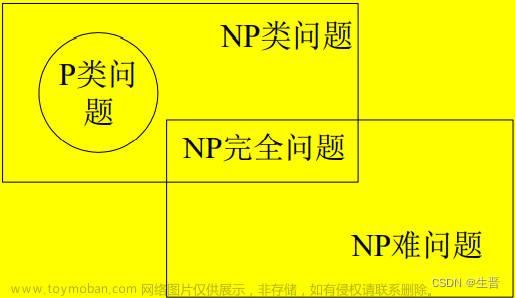
NP-hard问题： 假设存在这样一个问题，
1）任意np问题都可以在多项式时间内约化为该问题；
2）解决了该问题就解决了NP问题；这个问题就是NP-hard问题；
即 为了解决问题A，先将问题A约化为另一个问题B ， 解决问题B同时也间接解决了问题A。问题B就是一个NP-hard问题；
范围： 无多项式时间求解算法且不一定能在多项式时间内验证解的问题
例如，停机问题。
NPC问题：
理解一：如果存在一个问题可以在多项式时间内验证解的正确性，其他问题也可以约化为该问题，解决了该问题就解决了NP问题，该问题就是NPC问题。
理解二： 存在这样一个NP问题，所有的NP问题都可以约化成它。换句话说，只要解决了这个问题，那么所有的NP问题都解决了。
其定义要满足2个条件：
1） 首先它是一个NP问题；
2） 然后所有的NP问题都可以约化到它。文章来源：https://www.toymoban.com/news/detail-595671.html
范围： NPC问题既是NP问题，也是NP-hard问题。
文章来源地址https://www.toymoban.com/news/detail-595671.html
到了这里，关于NP-hard概念的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
