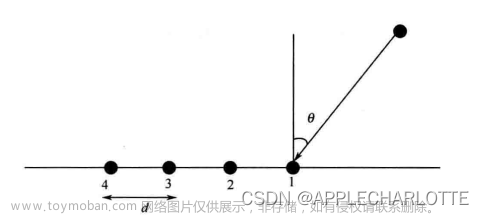
在阵列信号处理中,导向矢量矩阵(steering vector matrix)是描述阵列接收信号和信号源之间关系的重要工具。它用于计算不同到达角度(Direction of Arrival,DOA)下的阵列响应。
导向矢量矩阵是一个矩阵,其每一列代表一个特定的到达角度,而每一行代表阵列中的一个阵元。假设阵列由M个阵元组成,导向矢量矩阵的维度通常为M×L,其中L表示选择的离散角度的数量。
具体而言,对于给定的到达角度θ,导向矢量矩阵的第j列表示相对于第j个阵元的到达角度为θ的信号的复数权重。这个权重通常基于阵列的几何结构和阵元之间的距离。
导向矢量矩阵的构建方法取决于阵列的几何结构。以下是一些常见阵列结构的导向矢量矩阵计算示例:
-
线性阵列:对于线性阵列,阵元之间的间距为d,第j个阵元的导向矢量可表示为: a(j, θ) = [1, exp(-j2πdsin(θ)/λ), exp(-j2π2dsin(θ)/λ), ..., exp(-j2π(M-1)d*sin(θ)/λ)]^T 其中,λ表示信号波长。
-
均匀圆形阵列:对于均匀圆形阵列,阵元间距相等,构建导向矢量矩阵的方法类似于线性阵列,只是角度θ需要转换为极坐标形式。
-
矩形阵列:矩形阵列是一个二维阵列,阵元排列成矩形或方形。对于矩形阵列,需要计算阵列中每个阵元相对于指定到达角度的导向矢量。文章来源:https://www.toymoban.com/news/detail-595705.html
通过导向矢量矩阵,可以计算不同到达角度下阵列的响应。在DOA估计和波束成形等应用中,导向矢量矩阵与接收信号矩阵进行相关计算,从而实现对信号源的定位或波束形成。文章来源地址https://www.toymoban.com/news/detail-595705.html
到了这里,关于导向矢量矩阵(steering vector matrix)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!