【数学建模lingo学习】lingo解决规划问题1：投料问题-Toy模板网

这篇具有很好参考价值的文章主要介绍了【数学建模lingo学习】lingo解决规划问题1：投料问题。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

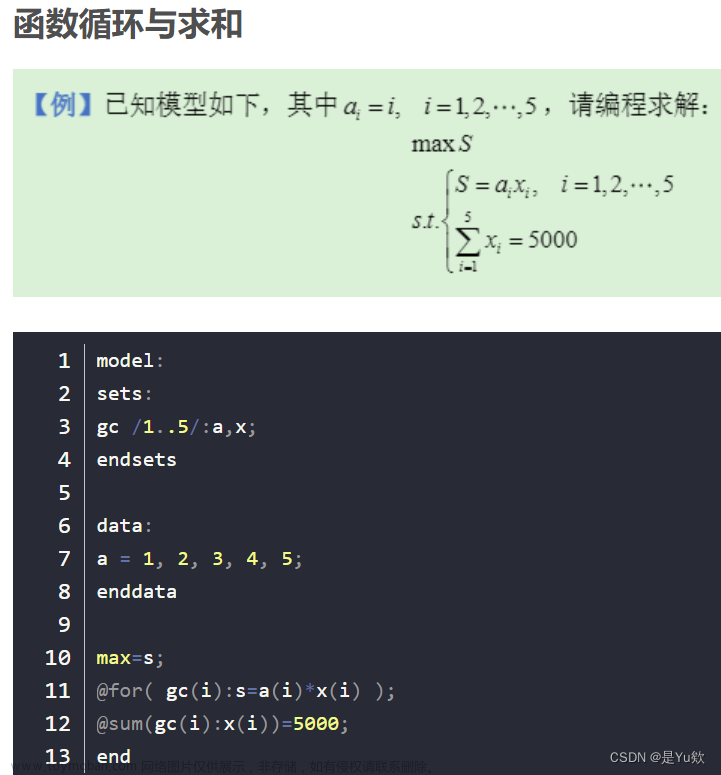
lingo相较于matlab实现规划问题更加简洁，但无法实现多目标规划，如果不了解lingo可以去看以下视频了解：

Lingo(1)：基础篇——基本界面与解方程_哔哩哔哩_bilibilihttps://www.bilibili.com/video/BV1CT4y177qS?spm_id_from=333.337.search-card.all.click那么废话不多说，我在这里分享一道例题及解法：

投料问题：

现有两个临时料场坐标分别为:A(5,1)，B(2,7);日储量各20吨
工地位置坐标及日需求量如下表所示：

	1	2	3	4	5	6
横坐标	1.25	8.75	0.5	5.75	3	7.25
纵坐标	1.25	0.75	4.75	5	6.5	7.25
日需求量	3	5	4	7	6	11

试制定每天的供应计划，即从两料场分别向各工地运送多少吨水泥，使总的吨千米数最小。

解设从第j个料场（j=1,2）送往第i(i=1,2,3...6)个工地的所需的水泥重量为xij吨,设工地的横坐标ai(i=1,2,3...6),纵坐标为bi(i=1,2,3...6)，料场的横坐标为xj(j=1,2),纵坐标为yj(j=1,2)每个料场的日需求量为di(i=1,2,3...6)

根据题目分析需要使总的吨千米数最小，则可设目标函数为：

糕点配料问题数学建模,学习,开发语言

由于每个工地的日需求量都有不同，可以得约束条件1:

糕点配料问题数学建模,学习,开发语言

由于两个料场的日存储量都为20吨，则有约束条件2：

糕点配料问题数学建模,学习,开发语言

由于往每个料场运送的吨数都为大于零的数，则有约束条件3：

糕点配料问题数学建模,学习,开发语言

lingo实现代码为

model:
!生成矩阵;
sets:
factory1/1..6/:a,b,d;
factory2/1..2/:x1,y1;
coo(factory1,factory2):x;
endsets

!输入题目中数据;
data:
!a,b表示工地坐标;
a=1.25,8.75,0.5,5.75,3,7.25;
b=1.25,0.75,4.75,5,6.5,7.25;
!x,y表示料场坐标;
x1=5,2;
y1=1,7;
!d表示工地日需求量;
d=3,5,4,7,6,11;


enddata
!列出表达式求解;
!目标函数;
min = @sum(coo(i,j):@sqrt((a(i)-x1(j))^2+(b(i)-y1(j))^2)*x(i,j));
!约束条件1;
@for(factory1(i):@sum(factory2(j):x(i,j))=d(i));
!约束条件2;
@for(factory2(j):@sum(factory1(i):x(i,j))<=20);

end

运行结果：

吨千米数最小为： 135.2815

需要往各个工地运送的物料如下表所示：文章来源地址https://www.toymoban.com/news/detail-597574.html