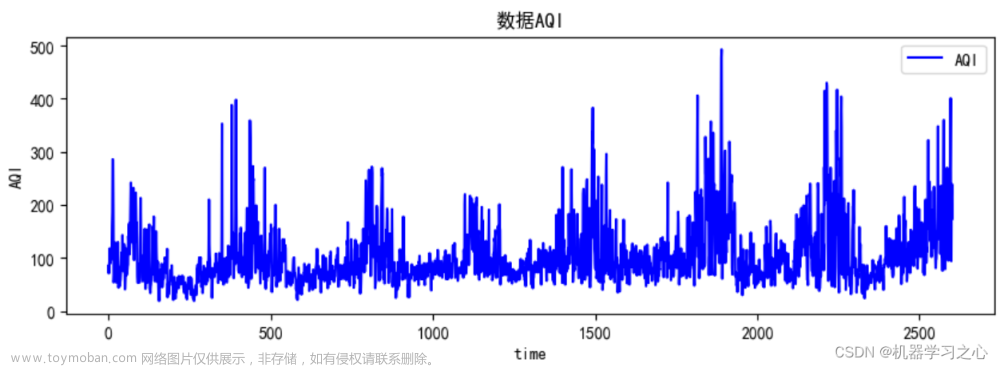
需要jar包Jama-1.0.2.jar,数据:时序数据的值 下载连接
https://download.csdn.net/download/dongyang1124/86265504文章来源地址https://www.toymoban.com/news/detail-598103.html
package arima;
import java.util.Vector;
public class ARMAModel
{
private double [] data = {};
private int p; //AR阶数
private int q; //MA阶数
public ARMAModel(double [] data, int p, int q)
{
this.data = data;
this.p = p;
this.q = q;
}
/**
* 在ARMA模型中,首先根据原始数据求得AR模型的自回归系数(AR系数)
* 利用AR系数与原始数据,求解的残差序列,根据残差序列的自协方差最终求得ARMA中MA系数
* @return ar, ma
*/
public Vector<double []> solveCoeOfARMA()
{
Vector<double []>vec = new Vector<>();
//ARMA模型
double [] armaCoe = new ARMAMethod().computeARMACoe(this.data, this.p, this.q);
//AR系数
double [] arCoe = new double[this.p + 1];
System.arraycopy(armaCoe, 0, arCoe, 0, arCoe.length);
//MA系数
double [] maCoe = new double[this.q + 1];
System.arraycopy(armaCoe, (this.p + 1), maCoe, 0, maCoe.length);
vec.add(arCoe);
vec.add(maCoe);
return vec;
}
}
package arima;
import java.util.Vector;
public class ARModel
{
private double [] data;
private int p;
public ARModel(double [] data, int p)
{
this.data = data;
this.p = p;
}
public Vector<double []> solveCoeOfAR()
{
Vector<double []>vec = new Vector<>();
double [] arCoe = new ARMAMethod().computeARCoe(this.data, this.p);
vec.add(arCoe);
return vec;
}
}
package arima;
import java.io.BufferedReader;
import java.io.File;
import java.io.FileInputStream;
import java.io.FileNotFoundException;
import java.io.IOException;
import java.io.InputStreamReader;
import java.nio.file.Path;
import java.nio.file.Paths;
import java.text.SimpleDateFormat;
import java.util.ArrayList;
import java.util.Date;
public class MainTest {
private static final SimpleDateFormat sdfWhole = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss");
public static void main(String args[]) {
Path path = Paths.get("./data/", "data_20220621.txt");
File file = path.toFile();
try (BufferedReader br = new BufferedReader(new InputStreamReader(
new FileInputStream(file)))) {
String line = null;
ArrayList<Double> al = new ArrayList<Double>();
while ((line = br.readLine()) != null) {
al.add(Double.parseDouble(line));
}
ArrayList<Double> samplingDataList = new ArrayList<>();
ArrayList<Double> comparisonDataList = new ArrayList<>();
System.out.println("开始时间"+sdfWhole.format(new Date()));
for (int i = 0; i < al.size(); i++) {
if (i < al.size() / 3 * 2) {
samplingDataList.add(al.get(i));
} else {
comparisonDataList.add(al.get(i));
}
}
for (double comData : comparisonDataList) {
double predict = predect(samplingDataList);
//System.out.println("Predict value=" + predict);
samplingDataList.add(predict);
/*System.out.println("Predict error=" + (predict - comData)
/ comData * 100 + "%");*/
}
System.out.println("结束时间"+sdfWhole.format(new Date()));
} catch (FileNotFoundException fnfe) {
fnfe.printStackTrace();
} catch (IOException ioe) {
ioe.printStackTrace();
}
}
/**
* 获取预测结果的值
*
* @param al
* @return
*/
public static double predect(ArrayList<Double> al) {
double[] data = null;
data = al.stream().mapToDouble(i -> i).toArray();
ARIMAModel arima = new ARIMAModel(data);
ArrayList<int[]> list = new ArrayList<>();
int period = 7;
int modelCnt = 3, cnt = 0;// 通过多次预测的平均值作为预测值
int[] tmpPredict = new int[modelCnt];
for (int k = 0; k < modelCnt; ++k) {// 控制通过多少组参数进行计算最终的结果
int[] bestModel = arima.getARIMAModel(period, list,
(k == 0) ? false : true);
if (bestModel.length == 0) {
tmpPredict[k] = (int) data[data.length - period];
cnt++;
break;
} else {
int predictDiff = arima.predictValue(bestModel[0],
bestModel[1], period);
tmpPredict[k] = arima.aftDeal(predictDiff, period);
cnt++;
}
list.add(bestModel);
}
double sumPredict = 0.0;
for (int k = 0; k < cnt; ++k) {
sumPredict += (double) tmpPredict[k] / (double) cnt;
}
double predict = (double) Math.round(sumPredict);
return predict;
}
}
package arima;
import java.util.Vector;
public class MAModel
{
private double [] data;
private int q;
public MAModel(double [] data, int q)
{
this.data = data;
this.q = q;
}
public Vector<double []> solveCoeOfMA()
{
Vector<double []>vec = new Vector<>();
double [] maCoe = new ARMAMethod().computeMACoe(this.data, this.q);
vec.add(maCoe);
return vec;
}
}
package arima;
import java.util.ArrayList;
import java.util.Random;
import java.util.Vector;
public class ARIMAModel
{
double [] originalData = {};
double [] dataFirDiff = {};
Vector<double []>arimaCoe = new Vector<>();
public ARIMAModel()
{
}
public ARIMAModel(double [] originalData)
{
this.originalData = originalData;
}
public double [] preFirDiff(double [] preData) //一阶差分(1)
{
double [] tmpData = new double[preData.length - 1];
for (int i = 0; i < preData.length - 1; ++i)
{
tmpData[i] = preData[i + 1] - preData[i];
}
return tmpData;
}
public double [] preSeasonDiff(double [] preData) //季节性差分(6, 7)
{
double [] tmpData = new double[preData.length - 7];
for (int i = 0; i < preData.length - 7; ++i)
{
tmpData[i] = preData[i + 7] - preData[i];
}
return tmpData;
}
public double [] preDealDiff(int period)
{
if (period >= originalData.length - 1) // 将6也归为季节性差分
{
period = 0;
}
switch (period)
{
case 0:
return this.originalData;
case 1:
this.dataFirDiff = this.preFirDiff(this.originalData);
return this.dataFirDiff;
default:
return preSeasonDiff(originalData);
}
}
public int [] getARIMAModel(int period, ArrayList<int []>notModel, boolean needNot)
{
double [] data = this.preDealDiff(period);
double minAIC = Double.MAX_VALUE;
int [] bestModel = new int[3];
int type = 0;
Vector<double []>coe = new Vector<>();
// model产生, 即产生相应的p, q参数
int len = data.length;
if (len > 5)
{
len = 5;
}
int size = ((len + 2) * (len + 1)) / 2 - 1;
int [][] model = new int[size][2];
int cnt = 0;
for (int i = 0; i <= len; ++i)
{
for (int j = 0; j <= len - i; ++j)
{
if (i == 0 && j == 0)
continue;
model[cnt][0] = i;
model[cnt++][1] = j;
}
}
for (int i = 0; i < model.length; ++i)
{
// 控制选择的参数
boolean token = false;
if (needNot)
{
for (int k = 0; k < notModel.size(); ++k)
{
if (model[i][0] == notModel.get(k)[0] && model[i][1] == notModel.get(k)[1])
{
token = true;
break;
}
}
}
if (token)
{
continue;
}
if (model[i][0] == 0)
{
MAModel ma = new MAModel(data, model[i][1]);
coe = ma.solveCoeOfMA();
type = 1;
}
else if (model[i][1] == 0)
{
ARModel ar = new ARModel(data, model[i][0]);
coe = ar.solveCoeOfAR();
type = 2;
}
else
{
ARMAModel arma = new ARMAModel(data, model[i][0], model[i][1]);
coe = arma.solveCoeOfARMA();
type = 3;
}
double aic = new ARMAMethod().getModelAIC(coe, data, type);
// 在求解过程中如果阶数选取过长,可能会出现NAN或者无穷大的情况
if (Double.isFinite(aic) && !Double.isNaN(aic) && aic < minAIC)
{
minAIC = aic;
bestModel[0] = model[i][0];
bestModel[1] = model[i][1];
bestModel[2] = (int)Math.round(minAIC);
this.arimaCoe = coe;
}
}
return bestModel;
}
public int aftDeal(int predictValue, int period)
{
if (period >= originalData.length)
{
period = 0;
}
switch (period)
{
case 0:
return (int)predictValue;
case 1:
return (int)(predictValue + originalData[originalData.length - 1]);
case 2:
default:
return (int)(predictValue + originalData[originalData.length - 7]);
}
}
public int predictValue(int p, int q, int period)
{
double [] data = this.preDealDiff(period);
int n = data.length;
int predict = 0;
double tmpAR = 0.0, tmpMA = 0.0;
double [] errData = new double[q + 1];
Random random = new Random();
if (p == 0)
{
if(null!=this.arimaCoe&&!this.arimaCoe.isEmpty()){
double [] maCoe = this.arimaCoe.get(0);
for(int k = q; k < n; ++k)
{
tmpMA = 0;
for(int i = 1; i <= q; ++i)
{
tmpMA += maCoe[i] * errData[i];
}
//产生各个时刻的噪声
for(int j = q; j > 0; --j)
{
errData[j] = errData[j - 1];
}
errData[0] = random.nextGaussian()*Math.sqrt(maCoe[0]);
}
}
predict = (int)(tmpMA);
}
else if (q == 0)
{
double [] arCoe = this.arimaCoe.get(0);
for(int k = p; k < n; ++k)
{
tmpAR = 0;
for(int i = 0; i < p; ++i)
{
tmpAR += arCoe[i] * data[k - i - 1];
}
}
predict = (int)(tmpAR);
}
else
{
double [] arCoe = this.arimaCoe.get(0);
double [] maCoe = this.arimaCoe.get(1);
for(int k = p; k < n; ++k)
{
tmpAR = 0;
tmpMA = 0;
for(int i = 0; i < p; ++i)
{
tmpAR += arCoe[i] * data[k- i - 1];
}
for(int i = 1; i <= q; ++i)
{
tmpMA += maCoe[i] * errData[i];
}
//产生各个时刻的噪声
for(int j = q; j > 0; --j)
{
errData[j] = errData[j-1];
}
errData[0] = random.nextGaussian() * Math.sqrt(maCoe[0]);
}
predict = (int)(tmpAR + tmpMA);
}
return predict;
}
}
package arima;
import java.util.Random;
import java.util.Vector;
import Jama.Matrix;
public class ARMAMethod
{
public ARMAMethod()
{
}
/**
* @param originalData
* @return 均值
*/
public double avgData(double [] originalData)
{
return this.sumData(originalData) / originalData.length;
}
/**
* @param originalData
* @return 求和
*/
public double sumData(double [] originalData)
{
double sum = 0.0;
for (int i = 0; i < originalData.length; ++i)
{
sum += originalData[i];
}
return sum;
}
/**
* 计算标准差 sigma = sqrt(var);
* @param originalData
* @return 标准差
*/
public double stdErrData(double [] originalData)
{
return Math.sqrt(this.varErrData(originalData));
}
/**
* 计算方差 var = sum(x - mu) ^2 / N;
* @param originalData
* @return 方差
*/
public double varErrData(double [] originalData)
{
if (originalData.length <= 1)
return 0.0;
double var = 0.0;
double mu = this.avgData(originalData);
for (int i = 0; i < originalData.length; ++i)
{
var += (originalData[i] - mu) * (originalData[i] - mu);
}
var /= (originalData.length - 1); //方差的无偏估计
return var;
}
/**
* 计算自相关函数(系数) rou(k) = C(k) / C(0);
* 其中 C(k) = sum((x(t) - mu)*(x(t - k) - mu)) / (N - k),
* C(0) = var = sum(x(t) - mu) ^2 / N;
* @param originalData
* @param order
* @return 自相关函数(rou(k))
*/
public double [] autoCorrData(double [] originalData, int order)
{
double [] autoCov = this.autoCovData(originalData, order);
double [] autoCorr = new double[order + 1]; //默认初始化为0
double var = this.varErrData(originalData);
if (var != 0)
{
for (int i = 0; i < autoCorr.length; ++i)
{
autoCorr[i] = autoCov[i] / var;
}
}
return autoCorr;
}
/**
* @param dataFir
* @param dataSec
* @return 皮尔逊相关系数(互相关)
*/
public double mutalCorr(double [] dataFir, double [] dataSec)
{
double sumX = 0.0;
double sumY = 0.0;
double sumXY = 0.0;
double sumXSq = 0.0;
double sumYSq = 0.0;
int len = 0;
if (dataFir.length != dataSec.length)
{
len = Math.min(dataFir.length, dataSec.length);
}
else
{
len = dataFir.length;
}
for (int i = 0; i < len; ++i)
{
sumX += dataFir[i];
sumY += dataSec[i];
sumXY += dataFir[i] * dataSec[i];
sumXSq += dataFir[i] * dataFir[i];
sumYSq += dataSec[i] * dataSec[i];
}
double numerator = sumXY - sumX * sumY / len;
double denominator = Math.sqrt((sumXSq - sumX * sumX / len) * (sumYSq - sumY * sumY / len));
if (denominator == 0)
{
return 0.0;
}
return numerator/ denominator;
}
/**
* @param data
* @return 互相关矩阵
*/
public double [][] computeMutalCorrMatrix(double [][] data)
{
double [][] result = new double[data.length][data.length];
for (int i = 0; i < data.length; ++i)
{
for (int j = 0; j < data.length; ++j)
{
result[i][j] = this.mutalCorr(data[i], data[j]);
}
}
return result;
}
/**
* 计算自协方差,C(k) = sum((x(t) - mu)*(x(t - k) - mu)) / (N - k);
* @param originalData
* @param order
* @return 自协方差(gama(k))-->认为是自相关系数
*/
public double [] autoCovData(double [] originalData, int order)
{
double mu = this.avgData(originalData);
double [] autoCov = new double[order + 1];
for (int i = 0; i <= order; ++i)
{
autoCov[i] = 0.0;
for (int j = 0; j < originalData.length - i; ++j)
{
autoCov[i] += (originalData[i + j] - mu) * (originalData[j] - mu);
}
autoCov[i] /= (originalData.length - i);
}
return autoCov;
}
/**
* @param vec 模型的系数
* @param data 数据
* @param type 选定的模型
* @return
*/
public double getModelAIC(Vector<double []>vec, double [] data, int type)
{
int n = data.length;
int p = 0, q = 0;
double tmpAR = 0.0, tmpMA = 0.0;
double sumErr = 0.0;
Random random = new Random();
/* MA */
if (type == 1)
{
double [] maCoe = vec.get(0);
q = maCoe.length;
double [] errData = new double[q];
for (int i = q - 1; i < n; ++i)
{
tmpMA = 0.0;
for (int j = 1; j < q; ++j)
{
tmpMA += maCoe[j] * errData[j];
}
for (int j = q - 1; j > 0; --j)
{
errData[j] = errData[j - 1];
}
errData[0] = random.nextGaussian() * Math.sqrt(maCoe[0]);
sumErr += (data[i] - tmpMA) * (data[i] - tmpMA);
}
// return Math.log(sumErr) + (q + 1) * 2 / n;
return (n - (q - 1)) * Math.log(sumErr / (n - (q - 1))) + (q + 1) * 2;
// return (n-(q-1))*Math.log(sumErr/(n-(q-1)))+(q)*Math.log(n-(q-1)); //AIC 最小二乘估计
}
/* AR */
else if (type == 2)
{
double [] arCoe = vec.get(0);
p = arCoe.length;
for (int i = p - 1; i < n; ++i)
{
tmpAR = 0.0;
for (int j = 0; j < p - 1; ++j)
{
tmpAR += arCoe[j] * data[i - j - 1];
}
sumErr += (data[i] - tmpAR) * (data[i] - tmpAR);
}
// return Math.log(sumErr) + (p + 1) * 2 / n;
return (n - (p - 1)) * Math.log(sumErr / (n - (p - 1))) + (p + 1) * 2;
// return (n-(p-1))*Math.log(sumErr/(n-(p-1)))+(p)*Math.log(n-(p-1)); //AIC 最小二乘估计
}
/* ARMA */
else
{
double [] arCoe = vec.get(0);
double [] maCoe = vec.get(1);
p = arCoe.length;
q = maCoe.length;
double [] errData = new double[q];
for (int i = p - 1; i < n; ++i)
{
tmpAR = 0.0;
for (int j = 0; j < p - 1; ++j)
{
tmpAR += arCoe[j] * data[i - j - 1];
}
tmpMA = 0.0;
for (int j = 1; j < q; ++j)
{
tmpMA += maCoe[j] * errData[j];
}
for (int j = q - 1; j > 0; --j)
{
errData[j] = errData[j - 1];
}
errData[0] = random.nextGaussian() * Math.sqrt(maCoe[0]);
sumErr += (data[i] - tmpAR - tmpMA) * (data[i] - tmpAR - tmpMA);
}
// return Math.log(sumErr) + (q + p + 1) * 2 / n;
return (n - (q + p - 1)) * Math.log(sumErr / (n - (q + p - 1))) + (p + q) * 2;
// return (n-(p-1))*Math.log(sumErr/(n-(p-1)))+(p+q-1)*Math.log(n-(p-1)); //AIC 最小二乘估计
}
}
// Y-W方程求解
/**
* @param garma 代表的是数据的协方差
* @return 返回经由Y-W方程求解的结果,其中最后数组的最后一个元素存储的是模型中的噪声方差
*/
public double [] YWSolve(double [] garma)
{
int order = garma.length - 1;
double [] garmaPart = new double[order];
System.arraycopy(garma, 1, garmaPart, 0, order);
// 将协方差转换为矩阵的形式
double [][] garmaArray = new double[order][order];
for (int i = 0; i < order; ++i)
{
// 对角线
garmaArray[i][i] = garma[0];
//下三角
int subIndex = i;
for (int j = 0; j < i; ++j)
{
garmaArray[i][j] = garma[subIndex--];
}
//上三角
int topIndex = i;
for (int j = i + 1; j < order; ++j)
{
garmaArray[i][j] = garma[++topIndex];
}
}
/* 调用了juma包,其实现了大部分对矩阵的操作 */
/* 可能会存在矩阵不可逆的情况,在矩阵不可逆时可以通过将对角线元素全部增加1e-6做修正 */
Matrix garmaMatrix = new Matrix(garmaArray);
Matrix garmaMatrixInverse = garmaMatrix.inverse();
Matrix autoReg = garmaMatrixInverse.times(new Matrix(garmaPart, order));
double [] result = new double[autoReg.getRowDimension() + 1];
for (int i = 0; i < autoReg.getRowDimension(); ++i)
{
result[i] = autoReg.get(i, 0);
}
double sum = 0.0;
for (int i = 0; i < order; ++i)
{
sum += result[i] * garma[i];
}
result[result.length - 1] = garma[0] - sum;
return result;
}
// Levinson 方法求解
/**
* @param garma 代表的是数据的协方差
* @return 返回结果的第一行元素代表的是在迭代过程中的方差,
* 其余的元素代表的是迭代过程中存储的系数
*/
public double [][] LevinsonSolve(double [] garma)
{
int order = garma.length - 1;
double [][] result = new double[order + 1][order + 1];
double [] sigmaSq = new double[order + 1];
sigmaSq[0] = garma[0];
result[1][1] = garma[1] / sigmaSq[0];
sigmaSq[1] = sigmaSq[0] * (1.0 - result[1][1] * result[1][1]);
for (int k = 1; k < order; ++k)
{
double sumTop = 0.0;
double sumSub = 0.0;
for (int j = 1; j <= k; ++j)
{
sumTop += garma[k + 1 - j] * result[k][j];
sumSub += garma[j] * result[k][j];
}
result[k + 1][k + 1] = (garma[k + 1] - sumTop) / (garma[0] - sumSub);
for (int j = 1; j <= k; ++j)
{
result[k + 1][j] = result[k][j] - result[k + 1][k + 1] * result[k][k + 1 - j];
}
sigmaSq[k + 1] = sigmaSq[k] * (1.0 - result[k + 1][k + 1] * result[k + 1][k + 1]);
}
result[0] = sigmaSq;
return result;
}
// 求解AR(p)的系数
/**
* @param originalData 原始数据
* @param p 模型的阶数
* @return AR模型的系数
*/
public double [] computeARCoe(double [] originalData, int p)
{
double [] garma = this.autoCovData(originalData, p); //p+1
double [][] result = this.LevinsonSolve(garma); //(p + 1) * (p + 1)
double [] ARCoe = new double[p + 1];
for (int i = 0; i < p; ++i)
{
ARCoe[i] = result[p][i + 1];
}
ARCoe[p] = result[0][p]; //噪声参数
// return this.YWSolve(garma);
return ARCoe;
}
// 求解MA(q)的系数
/**
* @param originalData 原始数据
* @param q 模型阶数
* @return MA系数
*/
public double [] computeMACoe(double [] originalData, int q)
{
// 确定最佳的p
// int p = 0;
// double minAIC = Double.MAX_VALUE;
// int len = originalData.length;
// for (int i = 1; i < len; ++i)
// {
// double [] garma = this.autoCovData(originalData, i);
// double [][] result = this.LevinsonSolve(garma);
//
// double [] ARCoe = new double[i + 1];
// for (int k = 0; k < i; ++k)
// {
// ARCoe[k] = result[i][k + 1];
// }
// ARCoe[i] = result[0][i];
double [] ARCoe = this.YWSolve(garma);
//
// Vector<double []> vec = new Vector<>();
// vec.add(ARCoe);
// double aic = this.getModelAIC(vec, originalData, 2);
// if (aic < minAIC)
// {
// minAIC = aic;
// p = i;
// }
// }
int p = (int)Math.log(originalData.length);
// System.out.println("The best p is " + p);
// 求取系数
double [] bestGarma = this.autoCovData(originalData, p);
double [][] bestResult = this.LevinsonSolve(bestGarma);
double [] alpha = new double[p + 1];
alpha[0] = -1;
for (int i = 1; i <= p; ++i)
{
alpha[i] = bestResult[p][i];
}
// double [] result = this.YWSolve(bestGarma);
// double [] alpha = new double[p + 1];
// alpha[0] = -1;
// for (int i = 1; i <= p; ++i)
// {
// alpha[i] = result[i - 1];
// }
double [] paraGarma = new double[q + 1];
for (int k = 0; k <= q; ++k)
{
double sum = 0.0;
for (int j = 0; j <= p - k; ++j)
{
sum += alpha[j] * alpha[k + j];
}
paraGarma[k] = sum / bestResult[0][p];
}
double [][] tmp = this.LevinsonSolve(paraGarma);
double [] MACoe = new double[q + 1];
for (int i = 1; i < MACoe.length; ++i)
{
MACoe[i] = -tmp[q][i];
}
MACoe[0] = 1 / tmp[0][q]; //噪声参数
// double [] tmp = this.YWSolve(paraGarma);
// double [] MACoe = new double[q + 1];
// System.arraycopy(tmp, 0, MACoe, 1, tmp.length - 1);
// MACoe[0] = tmp[tmp.length - 1];
return MACoe;
}
// 求解ARMA(p, q)的系数
/**
* @param originalData 原始数据
* @param p AR模型阶数
* @param q MA模型阶数
* @return ARMA模型系数
*/
public double [] computeARMACoe(double [] originalData, int p, int q)
{
double [] allGarma = this.autoCovData(originalData, p + q);
double [] garma = new double[p + 1];
for (int i = 0; i < garma.length; ++i)
{
garma[i] = allGarma[q + i];
}
double [][] arResult = this.LevinsonSolve(garma);
// AR
double [] ARCoe = new double[p + 1];
for (int i = 0; i < p; ++i)
{
ARCoe[i] = arResult[p][i + 1];
}
ARCoe[p] = arResult[0][p];
// double [] ARCoe = this.YWSolve(garma);
// MA
double [] alpha = new double[p + 1];
alpha[0] = -1;
for (int i = 1; i <= p; ++i)
{
alpha[i] = ARCoe[i - 1];
}
double [] paraGarma = new double[q + 1];
for (int k = 0; k <= q; ++k)
{
double sum = 0.0;
for (int i = 0; i <= p; ++i)
{
for (int j = 0; j <= p; ++j)
{
sum += alpha[i] * alpha[j] * allGarma[Math.abs(k + i - j)];
}
}
paraGarma[k] = sum;
}
double [][] maResult = this.LevinsonSolve(paraGarma);
double [] MACoe = new double[q + 1];
for (int i = 1; i <= q; ++i)
{
MACoe[i] = maResult[q][i];
}
MACoe[0] = maResult[0][q];
// double [] tmp = this.YWSolve(paraGarma);
// double [] MACoe = new double[q + 1];
// System.arraycopy(tmp, 0, MACoe, 1, tmp.length - 1);
// MACoe[0] = tmp[tmp.length - 1];
double [] ARMACoe = new double[p + q + 2];
for (int i = 0; i < ARMACoe.length; ++i)
{
if (i < ARCoe.length)
{
ARMACoe[i] = ARCoe[i];
}
else
{
ARMACoe[i] = MACoe[i - ARCoe.length];
}
}
return ARMACoe;
}
}
文章来源:https://www.toymoban.com/news/detail-598103.html
到了这里,关于ARIMA实现(亲测可用)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!