数据结构之List（双向链表）的实现-Toy模板网

这篇具有很好参考价值的文章主要介绍了数据结构之List（双向链表）的实现。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

链表要实现的对外方法

方法名	参数	功能	返回
find	const T & val, int n, listNode * p	区间查找从p往前数n个节点	指针或NULL
	const T & val, listNode * p	区间查找从p往前到首节点
	const T & val	查找
Size	void	链表规模	size
empty	void	判空	bool
first	void	返回首节点	首节点指针
clear	void	清空链表	void
insertAsFirst	const T & val	作为首节点插入	新节点指针
insertAsLast	const T & val	作为末节点插入
insertBefore	const T & val, listNode * node	在某节点前插入
insertAfter	const T & val, listNode * node	在某节点后插入
remove	listNode * node	移除	后一个节点的指针
unique	void	无序链表唯一化	删多少个
traverse	T2 & visit	遍历	void
unique_ordered	void	有序链表唯一化	删多少个
unique	void	无序链表唯一化	删多少个
unique	void	无序链表唯一化	删多少个
selectionSort	void	选择排序，范围全部	void
selectionSort	listNode* p, int n	范围从p往前数n个节点	void
insertionSort	void	插入排序，范围全部	void
insertionSort	listNode* p, int n	范围从p往前数n个节点	void

总结

函数的分割。插入操作就很方便。
在按指针遍历的循环中for (listNode<T> * p = head; p->succ != tail; p = p->succ，使用List<T>::remove()，是危险的。执行完remove(p)后，p将成为野指针。p=p->succ将发生错误。而Vector<T>::remove()是安全的。若非要执行remove(p)，请改成p = p->succ;remove(p->pred); 本程序中也可写为p = remove(p->pred);
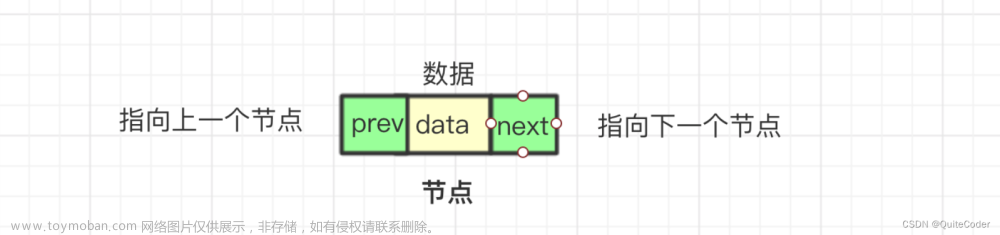
listNode为什么定义成struct而非class，因为List要经常对每个节点的前驱与后继做修改，所以pred、succ、data都是public的，所以listNode定义为struct
有序容器和无序容器的查找的区别在于，无序find()找不到返回NULL，有序search()可以返回失败位置。

code 链节

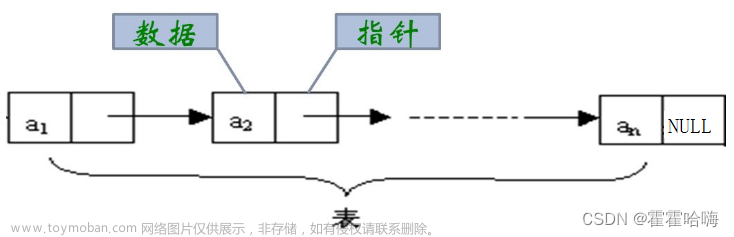
链表由节点连成，节点的定义如下文章来源地址https://www.toymoban.com/news/detail-598540.html

# pragma once
# include <iostream>

template <typename T>
struct listNode {
	T data;
	listNode <T>* pred;
	listNode <T>* succ;
	
	listNode(){}
	listNode(T d, listNode<T>* p, listNode<T>* s):data(d), pred(p), succ(s){}

	T getData(void) { return data; }
	listNode<T> getPred(void) { return pred; }
	listNode<T> getSucc(void) { return succ; }

	listNode <T>* insertAsPred(const T & e)
	{
		listNode <T> * tmp = new listNode <T>(e, pred, this);
		pred->succ = tmp;
		pred = tmp;
		return tmp;
	}

	listNode <T>* insertAsSucc(const T & e)
	{
		listNode <T> * tmp = new listNode <T>(e, this, succ);
		succ->pred = tmp;
		succ = tmp;
		return tmp;
	}
};

code 链表

# pragma once
# include "listNode.h"

template <typename T>
struct printList {
	void operator () (T* pnode)
	{
		std::cout << pnode->data << std::endl;
	}
};

template <typename T>
class List {
public:

	// 构造函数
	List() { init();}

	// 析构函数
	~List()
	{
		for (listNode<T> * currentNode = head->succ; currentNode; currentNode = currentNode->succ)
		{
			delete currentNode->pred;
		}
		delete tail;
	}

	//***********************************************************只读*********************************************************

	// 区间查找 从p往前数n个节点的范围
	listNode<T> * find(const T & val, int n, listNode<T> * p) const
	{
		while (n-- && p != head && p->data != val)
		{
			p = p->pred;
		}
		if (n == 0 && p == head) return NULL;
		else return p;
	}

	// 区间查找 从p往前到首节点的范围
	listNode<T> * find(const T & val, listNode<T> * p) const
	{
		while (p != head && p->data != val)
		{
			p = p->pred;
		}
		if (p == head) return NULL;
		else return p;
	}

	// 全体查找
	listNode<T> * find(const T & val) const
	{
		listNode<T> * find(val, tail->pred);
	}

	//***********************************************************可写*********************************************************

	// 清空
	void clear()
	{
		for (listNode<T> * currentNode = head->succ->succ; currentNode; currentNode = currentNode->succ)
		{
			delete currentNode->pred;
		}
		size = 0;
		head->pred = NULL;
		head->succ = tail;
		tail->pred = head;
		tail->succ = NULL;
	}

	// 作为首节点插入
	listNode<T> * insertAsFirst(const T & val) { ++size;  return head->insertAsSucc(val); }
	// 作为末节点插入
	listNode<T> * insertAsLast(const T & val) { ++size;  return tail->insertAsPred(val); }
	// 在某节点前插入
	listNode<T> * insertBefore(const T & val, listNode<T> * node) { ++size;  return node->insertAsPred(val); }
	// 在某节点后插入
	listNode<T> * insertAfter(const T & val, listNode<T> * node) { ++size;  return node->insertAsSucc(val); }

	// 移除
	listNode<T> * remove(listNode<T> * node)
	{
		if (node == NULL) return NULL;
		--size;
		listNode<T> * succNode = node->pred->succ = node->succ;
		node->succ->pred = node->pred;
		delete node;
		return succNode;
	}

	// 唯一化
	int unique(void)
	{
		int oldSize = size;
		for (listNode<T> * p = head->succ; p != tail; p = p->succ)
		{
			remove(find(p->data, p->pred));
		}
		return oldSize - size;
	}

	// 基于复制的构造

	//***********************************************************遍历*********************************************************
	template <typename T2> void traverse(T2 & visit)
	{
		for (listNode<T> * p = head->succ; p != tail; p = p->succ)
		{
			visit(p);
		}
	}

	//*****************************************************针对有序链表的操作***************************************************

	// 有序链表唯一化
	int unique_ordered(void)
	{
		// 如果该节点与前驱data一样，删掉前驱
		if (size < 2) return 0;
		int oldSize = size;
		for (listNode<T> *p = head->succ->succ; p != tail; p = p->succ)
		{
			if (p->data == p->pred->data)
			{
				remove(p->pred);
			}
		}
		return oldSize - size;
	}

	// 查找
	listNode<T> * search(const T & data, listNode<T> * p, int n)
	{
		while (n-- && p != head && data < p->data)
		{
			p = p->pred;
		}
		return p;
	}

	//***********************************************************排序*********************************************************
	
	// 插入排序
	void insertionSort(listNode<T>*p, int n);
	void insertionSort(void){ insertionSort(head->succ, size);}

	// 选择排序
	void selectionSort(listNode<T>*p, int n);
	void selectionSort(void) { selectionSort(head->succ, size);}

protected:

	// 初始化双向链表
	void init(void)
	{
		size = 0;
		head = new listNode<T>;
		tail = new listNode<T>;
		head->pred = NULL;
		head->succ = tail;
		tail->pred = head;
		tail->succ = NULL;
	}

	// 从p开始往前找n个，这些data之中最大的，且最右的
	listNode<T>* Max(listNode<T>* p, int n);

private:
	listNode<T> * head;
	listNode<T> * tail;
	int size;

};

// 选择排序
template <typename T>
void List<T>::selectionSort(listNode<T>*p, int n)
{
	// 找到有序后缀（注意，初始长度为0）
	listNode<T>* pos = p; //一会儿要在pos之前插入
	for (int i = 1; i <= n; ++i) pos = pos->succ;

	for (int rank = 0; rank < n; ++rank, pos = pos->pred) //有序后缀的长度
	{
		// 找前缀中最大值
		listNode<T> * tmp_max = Max(pos->pred, n - rank);

		// 插入后缀最前面
		insertBefore(tmp_max->data, pos);
		remove(tmp_max);
	}
}

// 从p开始往前找n个，这些data之中最大的，且最右的
template <typename T>
listNode<T>* List<T>::Max(listNode<T>* p, int n)
{
	listNode<T> * tmp_max = p;
	while (n-- && p != head)
	{
		if (p->data > tmp_max->data) tmp_max = p;
		p = p->pred;
	}
	return tmp_max;
}

// 插入排序
template <typename T>
void List<T>::insertionSort(listNode<T>*p, int n)
{
	for (int rank = 1; rank <= n; ++rank) //有序前缀的长度
	{
		listNode<T>* pos = search(p->data, p->pred, rank);
		insertAfter(p->data, pos);
		//p = p->succ;
		p = remove(p->pred);
	}
}