1917年,Radon 变换被提出。例如一个三维物体,如果知道它在各个方向的平面投影,能不能推出它的精确形状,这个数学问题可以由拉东变换解决。
拉东变换
R n R^n Rn 上实值函数的拉东变换定义为 n - 1 n - 1 n-1 维超平面上的积分值,它是由拉东引入的. 拉东变换与从函数在空间 R n R^n Rn 的所有超平面上计算的积分值去还原该函数的问题直接相联系(即拉东变换反演问题).
拉东变换以及特别是相应的反演公式(即从函数 f f f 的拉东变换还原 f f f 的公式)在断层照相法中具有最关键的重要性。拉东变换是调和分析和积分几何领域中的重要课题. 它与 Fourier 变换、Laplace 算子和球面调和函数有着密切的联系.
R 2 R^2 R2 上的拉东变换
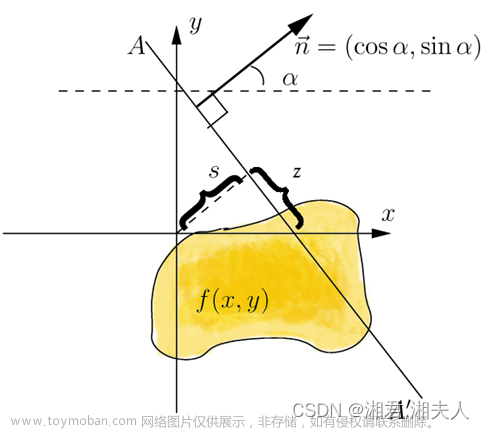
定义平面上函数 f ( x , y ) f(x,y) f(x,y) 的拉东变换为 R f ( L ) = ∫ L f ( x , y ) d s Rf(L)=\int_L f(x,y)ds Rf(L)=∫Lf(x,y)ds ,由积分学的知识, ∫ L f ( x , y ) d s \int_L f(x,y) ds ∫Lf(x,y)ds 表示函数 f ( x , y ) f(x,y) f(x,y) 在积分路径 L L L 上的第一型曲线积分。
若光滑曲线 L : { x = φ ( t ) y = ψ ( t ) , t ∈ [ α , β ] L:\begin{cases} x=\varphi(t)\\ y=\psi(t) \end{cases},t\in[\alpha,\beta] L:{x=φ(t)y=ψ(t),t∈[α,β],函数 f ( x , y ) f(x,y) f(x,y) 为定义在 L L L 上的连续函数,则 ∫ L f ( x , y ) d s = ∫ α β f ( φ ( t ) , ψ ( t ) ) [ φ ‘ ( t ) ] 2 + [ ψ ‘ ( t ) ] 2 d t . \int_L f(x,y) ds=\int_\alpha^\beta f(\varphi(t),\psi(t))\sqrt{[\varphi^`(t)]^2+[\psi^`(t)]^2} dt. ∫Lf(x,y)ds=∫αβf(φ(t),ψ(t))[φ‘(t)]2+[ψ‘(t)]2dt.
令 L L L 表示平面上任何一条直线,方差 ℓ t , θ : x cos θ + y sin θ = t \ell_{t,\theta}:x\cos \theta +y\sin \theta=t ℓt,θ:xcosθ+ysinθ=t,它的位置由两个参数 ( t , θ ) (t,\theta) (t,θ) 来决定,其中 t t t 表示向量 X = ( x , y ) X=(x,y) X=(x,y) 在单位向量 n → = ( cos θ , sin θ ) \overrightarrow{n}=(\cos \theta,\sin \theta) n=(cosθ,sinθ) 上的投影,即 X ⋅ n → = t . X\cdot \overrightarrow{n}=t. X⋅n=t. 将单位向量 n → = ( cos θ , sin θ ) \overrightarrow{n}=(\cos \theta,\sin \theta) n=(cosθ,sinθ) 逆时针旋转 90 度得到单位向量 n → ⊥ = ( − sin θ , cos θ ) \overrightarrow{n}^\perp=(-\sin \theta,\cos \theta) n⊥=(−sinθ,cosθ),记 X ⋅ n → ⊥ = t . X\cdot \overrightarrow{n}^\perp=t. X⋅n⊥=t. 由 X = t n ⃗ + s n ⃗ ⊥ X=t\vec n+s\vec n ^\perp X=tn+sn⊥,得直线 L L L 以 s s s 为参数的参数方程: { x = t cos θ − s sin θ y = t sin θ + s cos θ . \begin{cases} x=t\cos \theta-s\sin \theta \\ y=t\sin \theta+ s\cos \theta \end{cases}. {x=tcosθ−ssinθy=tsinθ+scosθ.
定义:设函数 f ( x , y ) f(x,y) f(x,y) 沿平面上任意一条直线 ℓ t , θ : x cos θ + y sin θ = t \ell_{t,\theta}:x\cos \theta +y\sin \theta=t ℓt,θ:xcosθ+ysinθ=t,称 R f ( t , θ ) = ∫ − ∞ + ∞ f ( t cos θ − s sin θ , t sin θ + s cos θ ) d s Rf(t,\theta)=\int_{-\infin}^{+\infin}f(t\cos \theta-s\sin \theta,t\sin \theta + s \cos \theta)ds Rf(t,θ)=∫−∞+∞f(tcosθ−ssinθ,tsinθ+scosθ)ds 为函数 f ( x , y ) f(x,y) f(x,y) 的拉东变换。
- 习惯上称
∫
L
f
(
x
,
y
)
d
s
\int_L f(x,y) ds
∫Lf(x,y)ds 为投影值。当
θ
=
0
\theta=0
θ=0 时,
R
f
(
t
,
0
)
=
∫
−
∞
+
∞
f
(
x
,
y
)
d
y
Rf(t,0)=\int_{-\infin}^{+\infin}f(x,y)dy
Rf(t,0)=∫−∞+∞f(x,y)dy 表示在
x
x
x 轴的投影;当
θ = π 2 \theta=\frac \pi 2 θ=2π时, R f ( t , π 2 ) = ∫ − ∞ + ∞ f ( x , y ) d x Rf(t,\frac \pi 2)=\int_{-\infin}^{+\infin}f(x,y)dx Rf(t,2π)=∫−∞+∞f(x,y)dx 表示在 y y y 轴的投影。 - 从形式上看, R f ( t , θ ) Rf(t,\theta ) Rf(t,θ) 是一个无穷区间上的广义积分,但在实际应用中函数 f ( x , y ) f(x,y) f(x,y) 有紧支集,即在某个圆外为零,广义积分变成了特定区间上的定积分。
拉东变换的性质
(1)平移性
若
f
(
x
,
y
)
=
g
(
x
−
a
,
y
−
b
)
f(x,y)=g(x-a,y-b)
f(x,y)=g(x−a,y−b),则
R
f
(
t
,
θ
)
=
R
g
(
t
−
a
cos
θ
−
b
sin
θ
,
θ
)
Rf(t,\theta)=Rg(t-a\cos \theta-b\sin \theta , \theta)
Rf(t,θ)=Rg(t−acosθ−bsinθ,θ).
(2)旋转性
若
f
(
x
,
y
)
=
g
(
x
cos
φ
−
y
sin
φ
,
x
sin
φ
+
y
cos
φ
)
f(x,y)=g(x\cos \varphi - y\sin \varphi, x\sin \varphi + y \cos \varphi)
f(x,y)=g(xcosφ−ysinφ,xsinφ+ycosφ),则
R
f
(
t
,
θ
)
=
R
g
(
t
,
θ
+
φ
)
.
Rf(t,\theta)=Rg(t,\theta+\varphi).
Rf(t,θ)=Rg(t,θ+φ).
(3)伸缩性
若
c
≠
0
,
f
(
x
,
y
)
=
g
(
c
s
,
c
y
)
c\not =0,f(x,y)=g(cs,cy)
c=0,f(x,y)=g(cs,cy),则
R
f
(
t
,
θ
)
=
1
∣
c
∣
R
g
(
c
t
,
θ
)
.
Rf(t,\theta)=\frac 1 {|c|}Rg(ct,\theta).
Rf(t,θ)=∣c∣1Rg(ct,θ).
(4)线性
R
(
a
f
+
b
g
)
(
t
,
θ
)
=
a
R
f
(
t
,
θ
)
+
b
R
g
(
t
,
θ
)
.
R(af+bg)(t,\theta)=aRf(t,\theta)+bRg(t,\theta).
R(af+bg)(t,θ)=aRf(t,θ)+bRg(t,θ).
R 2 R^2 R2 上的拉东变换的逆变换
固定 θ \theta θ,将 R f ( t , θ ) Rf(t,\theta) Rf(t,θ) 的一维傅里叶变换(关于变量 t t t) 写为 R ^ f ( w , θ ) = ∫ − ∞ + ∞ R f ( t , θ ) e − i w t d t = ∫ − ∞ + ∞ ∫ − ∞ + ∞ f ( t cos θ − s sin θ , t sin θ + s cos θ ) d s e − i w t d t = ∫ − ∞ + ∞ ∫ − ∞ + ∞ f ( x , y ) e − i w ( x cos θ + y sin θ ) d x d y = ∫ − ∞ + ∞ ∫ − ∞ + ∞ f ( x , y ) e − i ( x , y ) ⋅ ( w cos θ , w sin θ ) d x d y = f ^ ( w cos θ , w sin θ ) \hat Rf(w,\theta)=\int_{-\infin}^{+\infin}Rf(t,\theta)e^{-iwt}dt=\int_{-\infin}^{+\infin}\int_{-\infin}^{+\infin}f(t\cos \theta-s \sin \theta,t \sin \theta + s \cos \theta)ds\space e^{-iwt}dt \\=\int_{-\infin}^{+\infin}\int_{-\infin}^{+\infin}f(x,y)e^{-iw(x\cos \theta+y\sin \theta)} dxdy =\int_{-\infin}^{+\infin}\int_{-\infin}^{+\infin}f(x,y)e^{-i(x,y)\cdot (w \cos \theta , w \sin \theta)}dxdy=\hat f(w \cos \theta,w\sin \theta) R^f(w,θ)=∫−∞+∞Rf(t,θ)e−iwtdt=∫−∞+∞∫−∞+∞f(tcosθ−ssinθ,tsinθ+scosθ)ds e−iwtdt=∫−∞+∞∫−∞+∞f(x,y)e−iw(xcosθ+ysinθ)dxdy=∫−∞+∞∫−∞+∞f(x,y)e−i(x,y)⋅(wcosθ,wsinθ)dxdy=f^(wcosθ,wsinθ)这表明对图像投影 R f ( t , θ ) Rf(t,\theta) Rf(t,θ) 的一维傅里叶变换(关于变量 t t t) 等于对图像 f ( x , y ) f(x,y) f(x,y) 的二维傅里叶变换,称为中心切片定理.文章来源:https://www.toymoban.com/news/detail-598841.html
图像重构就是求投影 R f ( t , θ ) Rf(t,θ) Rf(t,θ) 的逆变换(反演变换). 对一切 ( t , θ ) (t,θ) (t,θ) 值知道了函数 f ( x , y ) f(x,y) f(x,y) 的拉东变换时,相当于知道了函数 f ( x , y ) f(x,y) f(x,y) 的二维傅里叶变换,因此对 f ^ ( ω c o s θ , ω s i n θ ) \hat f(ωcosθ,ωsinθ) f^(ωcosθ,ωsinθ) 作傅里叶逆变换,从而得到拉东变换的逆变换: f ( x , y ) = 1 4 π 2 ∫ − ∞ + ∞ ∫ − ∞ + ∞ f ^ ( u , v ) e i ( u x + v y ) d u d v = 1 4 π 2 ∫ 0 2 π ∫ 0 + ∞ f ^ ( w cos θ , w sin θ ) e i w ( x cos θ + y sin θ ) w d w d θ = 1 4 π 2 ∫ 0 2 π ∫ 0 + ∞ R ^ f ( w , θ ) e i w ( x cos θ + y sin θ ) w d w d θ . f(x,y)=\frac 1 {4\pi^2}\int_{-\infin}^{+\infin}\int_{-\infin}^{+\infin}\hat f(u,v)e^{i(ux + vy)}dudv\\ =\frac 1 {4\pi^2}\int_{0}^{2\pi}\int_{0}^{+\infin}\hat f(w\cos \theta,w\sin \theta)e^{iw(x\cos \theta + y\sin \theta)} w \space dwd\theta \\=\frac 1 {4\pi^2}\int_{0}^{2\pi}\int_{0}^{+\infin}\hat Rf(w,\theta)e^{iw(x\cos \theta + y\sin \theta)}w\space dwd\theta. f(x,y)=4π21∫−∞+∞∫−∞+∞f^(u,v)ei(ux+vy)dudv=4π21∫02π∫0+∞f^(wcosθ,wsinθ)eiw(xcosθ+ysinθ)w dwdθ=4π21∫02π∫0+∞R^f(w,θ)eiw(xcosθ+ysinθ)w dwdθ.文章来源地址https://www.toymoban.com/news/detail-598841.html
到了这里,关于拉东(Radon)变换的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!