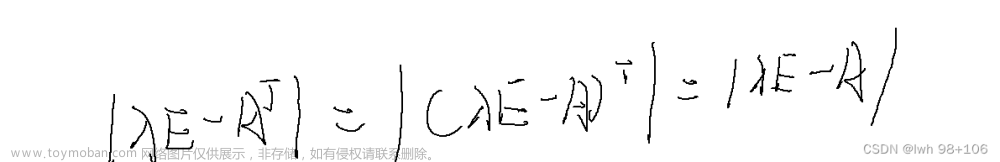6.7 广义特征向量与特征空间-Toy模板网

这篇具有很好参考价值的文章主要介绍了6.7 广义特征向量与特征空间。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

之前把广义特征向量放在特征值的第一篇文章里，我后来觉得对初学者太不友好了，所以剪出来，单独作为一篇文章。

1 特征空间

前面说过矩阵不过是把自己的特征向量给延长或缩短了，为了求特征值和特征向量，我们有以下的方程：
$(A-\lambda I)v=0$
把某个特征值代进去，得到的 $A-\lambda I$ 是一个矩阵，这个矩阵会把对应的特征向量变成0向量。这群向量构成了一个空间，这个空间就叫做特征空间。
可以举个例子：
$A=\begin{pmatrix} 2.0 & 1.0 & -1.0\\ 1.0 & 2.0 & -1.0\\ -1.0 & -1.0 & 2.0 \end{pmatrix}\\ A-\lambda I=\begin{pmatrix} 1.0 & 1.0 & -1.0\\ 1.0 & 1.0 & -1.0\\ -1.0 & -1.0 & 1.0 \end{pmatrix}\\$
然后我们根据定义解下齐次线性方程组就可以了。
$\begin{pmatrix} 1.0 & 1.0 & -1.0\\ 1.0 & 1.0 & -1.0\\ -1.0 & -1.0 & 1.0 \end{pmatrix} \sim \begin{pmatrix} 1.0 & 1.0 & -1.0\\ 0.0 & 0.0 & 0.0\\ 0.0 & 0.0 & 0.0 \end{pmatrix}\\ \therefore v=k_1\begin{pmatrix}1\\0\\1\end{pmatrix}+k_2\begin{pmatrix}0\\1\\1\end{pmatrix}$
所以这个特征空间的两个基就求出来了。我们再试一下下一个特征值4：
$A=\begin{pmatrix} 2.0 & 1.0 & -1.0\\ 1.0 & 2.0 & -1.0\\ -1.0 & -1.0 & 2.0 \end{pmatrix}\\ A-\lambda I=\begin{pmatrix} -2.0 & 1.0 & -1.0\\ 1.0 & -2.0 & -1.0\\ -1.0 & -1.0 & -2.0 \end{pmatrix}\\$
同样，解一下这个齐次方程组：
$\begin{pmatrix} -2.0 & 1.0 & -1.0\\ 1.0 & -2.0 & -1.0\\ -1.0 & -1.0 & -2.0 \end{pmatrix} \sim \begin{pmatrix} -2.0 & 1.0 & -1.0\\ 0.0 & 1.0 & 1.0\\ 0.0 & 0.0 & 0.0 \end{pmatrix}\\ \therefore v=k\begin{pmatrix}0\\1\\1\end{pmatrix}$
这样两个特征值的特征空间就求出来了。

2 广义特征向量

有了特征向量和特征向量构成的特征空间，我们知道 $A-\lambda I$ 可以把特征空间里的向量变成0。我们再想想， $(A-\lambda I)^2$ 能不能把某个向量变成0呢？三次方呢？四次方呢？有了方向，数学家们就开始思考了，于是有了广义特征向量的定义：
$(A-\lambda I)^jv=0$
公式中v被成为广义特征向量generalized eigenvector,对于某个固定的v，上述公式中的 $j$ 的最小值是广义特征向量的下标index。毫无疑问,特征向量本身是一个j=1的广义特征向量。我们举个例子：
$\begin{pmatrix} 2 & 1 & 1\\ -2 & -1 & -2\\ 1 & 1 & 2 \end{pmatrix}\\ \lambda=1$
以 $\lambda_1=2$ 为例子，求它的特征方程：
$A=\begin{pmatrix} 3 & 1 & 1\\ -2 & 0 & -2\\ 1 & 1 & 3 \end{pmatrix} \\ A-2I= \begin{pmatrix} 1 & 1 & 1\\ -2 & -2 & -2\\ 1 & 1 & 1 \end{pmatrix} \sim \begin{pmatrix} 1 & 1 & 1\\ 0 & 0 & 0\\ 0 & 0 & 0 \end{pmatrix}\\ v=k_1\begin{pmatrix}-1\\1\\0\end{pmatrix}+k_2\begin{pmatrix}-1\\0\\1\end{pmatrix}\\ (A-2I)^2= \begin{pmatrix} 0 & 0 & 0\\ 0 & 0 & 0\\ 0 & 0 & 0 \end{pmatrix}\\ v=k_1\begin{pmatrix}1\\0\\0\end{pmatrix}+k_2\begin{pmatrix}0\\1\\0\end{pmatrix}+k_3\begin{pmatrix}0\\0\\1\end{pmatrix}\\$
所以j到2时，再乘什么都是0矩阵了，广义特征向量就是任意向量，再乘方就没意义了。

3 广义特征空间

对于上述的规律，我们总在j增大到一定程度后，广义特征向量所在的空间是不会增大的。所以对某个特定的特征值定义了以下空间：
$E_j(\lambda)=\{v|(A-\lambda I)^jv=0\}$
当 $j$ 无穷大时定义的空间 $E_\infty(\lambda)$ ，被称为广义特征空间generalized eigenspace。但是也不要看到无穷就悲观，因为前面我们说了当j到一定程度时， $E_j(\lambda)$ 空间不再扩大，这个时候就等于广义特征空间，这时候的 $j$ 被称为广义特征向量最大下标maximum index of
a generalized eigenvector of A associated to λ,数学符号为 $ma x$ - $ind(\lambda)$ 。实际上 $ma x$ - $ind(\lambda)$ 等于该特征值最大约当块的行数。所以利用这个特性，可以快速确定矩阵的约当标准型。如下面的矩阵：
$\begin{pmatrix} 2 & 1 & -1\\ 1 & 2 & -1\\ -1 & -1 & 2 \end{pmatrix}\\ \lambda_1=\lambda_2=1,\lambda_3=4$
它的约当标准型有两种可能：
$\begin{pmatrix} 1 & 1 & 0\\ 0 & 1& 0\\ 0 & 0 & 4 \end{pmatrix}or \begin{pmatrix} 1 & 0 & 0\\ 0 & 1& 0\\ 0 & 0 & 4 \end{pmatrix}$
那么到底是哪一种？这个时候就需要用特征空间了，求出 $ma x$ - $in d (1)$ 。那只能拿特征方程计算下呗：
$A-\lambda I=\begin{pmatrix} 1 & 1 & -1\\ 1 & 1 & -1\\ -1 & -1 & 1 \end{pmatrix} \sim \begin{pmatrix} 1 & 1 & -1\\ 0 & 0 & 0\\ 0 & 0 & 0\end{pmatrix}\\ (A-\lambda I)^2=\begin{pmatrix} 3 & 3 & -3\\ 3 & 3 & -3\\ -3 & -3 & 3 \end{pmatrix}\sim \begin{pmatrix} 1 & 1 & -1\\ 0 & 0 & 0\\ 0 & 0 & 0 \end{pmatrix}\\$
特征方程的二次方并没有变成0矩阵，说明 ${max}$ - ${ind}(1)=1$ ，所以约当标准型为：
$\begin{pmatrix} 1 & 0 & 0\\ 0 & 1& 0\\ 0 & 0 & 4 \end{pmatrix}$ 文章来源地址https://www.toymoban.com/news/detail-599054.html