P1387 最大正方形题解-Toy模板网

这篇具有很好参考价值的文章主要介绍了P1387 最大正方形题解。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

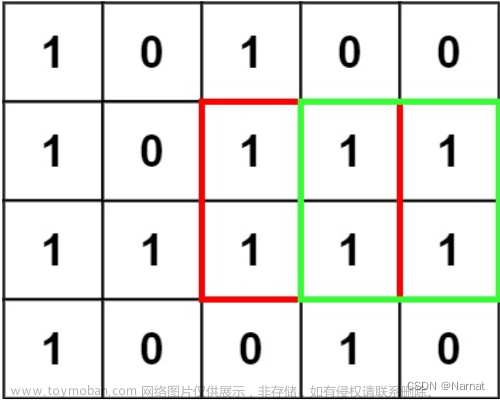
方法1 二分+暴力+前缀和Check

注意细节

通过二维前缀和判定矩形内是否全为1，计算和等于长度的平方就判断为是

复杂度\(\Theta (n^2\log{n})\)

#include <bits/stdc++.h>

#define N (int)(105)

using namespace std;

int mp[N][N];
int s[N][N];
int n,m;

bool check(int lenth)
{
	for(int i = 1;i + lenth - 1 <= n;i++)
	{
		for(int j = 1;j + lenth - 1 <= m;j++)
		{
			if(s[i + lenth - 1][j + lenth - 1] - s[i-1][j + lenth - 1] - s[i + lenth - 1][j-1] + s[i-1][j-1] == lenth * lenth)//
			{
				return true;
			}
		}
	}
	return false;
}

int main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin >> n >> m;
	for(int i = 1;i <= n;i++)
	{
		for(int j =1;j <= m;j++)
		{
			cin >> mp[i][j];
			s[i][j] = s[i-1][j] + s[i][j-1] - s[i-1][j-1] + mp[i][j];
		}
	}
	
	int l = 1, r = min(n,m);
	while(l < r)
	{
		int mid = (l + r) / 2 + 1;
		if(check(mid)) l = mid;
		else r = mid - 1;
	}
	cout << l;
	return 0;
}

方法2 DP

设状态\(f_{i,j}\)为以第\(i\)行\(j\)列为右下角的最大正方形的边长,\(a_{i,j}\)表示输入矩阵中的数值，有转移方程：

\[f_{i,j} = (min(f_{i-1,j},f_{i,j-1},f_{i-1,j-1}) + 1) * a_{i,j} \]

解释：考虑\(a_{i,j}\)为0，那么\(f_{i,j}\)为零是正确的。

\(a_{i,j}\)不为0，那么最少边长就是1，考虑像上向右延伸边，由于正方形的相关性质，取可以延伸的宽和高的最小，可以延伸的高就是\(min(f_{i-1,j},f_{i-1,j-1})\), 可延伸的宽就是\(min(f_{i,j-1},f_{i-1,j-1})\)。这样就解释完了。

不过我们可以逆向思考一下如何想出这种DP，首先我们是拿一块已经确定了的正方形然后考虑如何将它拓展（刷表思路）；或者我们思考如何将其他正方形的交拼成一个新的正方形（填表思路）。

我们画出一幅由1（或者0）组成的地图，并在其中寻找正方形。（建议画图）

刷表思路：我们考虑将一个正方形扩展到它右下一格的位置，那么我们发现，根据状态的定义，右下正方形最大边长，就是1加上当前最大正方形的边长，更长的边长是不支持的。然后我们发现还需要两个条件，就是下侧和右侧两个“条”状部位需要全部都是1，那么这里就可以推出\(min\)的使用了。可见思考\(min\)可以先固定化一部分，再想另一部分。

填表思路：我们考虑以一个位置为右下角、某个固定大小的正方形，如何用三个正方形把它拼出来（取交集），实际上我们发现，我们把右下角刨去之后，观察剩下的部分，需要\(f_{i-1,j},f_{i,j-1},f_{i-1,j-1}\)综合判断，不能缺在边上(\(f_{i-1,j},f_{i,j-1},\))，也不能缺在左上角(\(f_{i-1,j-1}\))，对于这三个量的贡献，我们固定其他两个，看其中一个，都能够发现\(min\)的贡献关系。文章来源地址https://www.toymoban.com/news/detail-599104.html

总结：设置状态的时候占右下角，是为了带最优性质和推理基础；转移的时候从具体例子考虑。

#include <bits/stdc++.h>

#define N (int)(105)

using namespace std;

int mp[N][N];
int f[N][N];
int n,m,ans;

int main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin >> n >> m;
	for(int i = 1;i <= n;i++)
	{
		for(int j = 1;j <= m;j++)
		{
			cin >> mp[i][j];
		}
	}
	for(int i = 1;i <= n;i++)
	{
		for(int j = 1;j <= m;j++)
		{
			f[i][j] = (min(min(f[i-1][j-1],f[i-1][j]),f[i][j-1]) + 1) * mp[i][j];
			ans = max(ans,f[i][j]);
		}
	}
	cout << ans;
	
	return 0;
}

到了这里，关于P1387 最大正方形题解的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！