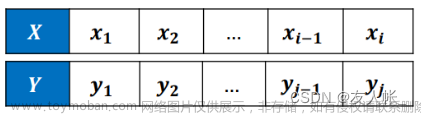
最长公共子序列,英文缩写为LCS(Longest Common Subsequence)。其定义是,一个序列 S ,如果分别是两个或多个已知序列的子序列,且是所有符合此条件序列中最长的,则 S 称为已知序列的最长公共子序列。
子串、子序列还有公共子序列的概念(在上篇LIS中也曾涉及过) ,我们以字符子串和字符子序列为例,更为形象,也能顺带着理解字符的子串和子序列:
(1)字符子串:指的是字符串中连续的n个字符,如abcdefg中,ab,cde,fg等都属于它的字串。 (2)字符子序列:指的是字符串中不一定连续但先后顺序一致的n个字符,即可以去掉字符串中的部分字符,但不可改变其前后顺序。如abcdefg中,acdg,bdf属于它的子序列,而bac,dbfg则不是,因为它们与字符串的字符顺序不一致。 (3) 公共子序列:如果序列C既是序列A的子序列,同时也是序列B的子序列,则称它为序列A和序列B的公共子序列。如对序列 1,3,5,4,2,6,8,7和序列 1,4,8,6,7,5 来说,序列1,8,7是它们的一个公共子序列。 那么现在,我们再通俗的总结一下最长公共子序列(LCS):就是A和B的公共子序列中长度最长的(包含元素最多的)
其实从上面的对比,我们不难发现公共子序列不严格要求其公共部分是连续的,只要其出现的先后顺序是一致即可,同上方1,3,5,4,2,6,8,7和序列1,4,8,6,7,5;序列1,8,7都是1先出现,8后出现,7最后出现。
仍然用序列1,3,5,4,2,6,8,7和序列1,4,8,6,7,5为例,它们的最长公共子序列有1,4,8,7和1,4,6,7两种,但最长公共子序列的长度是4。由此可见,最长公共子序列(LCS)也不一定唯一。
动态规划解决最长子序列思路
概念描述:
解决LCS问题,需要把原问题分解成若干个子问题,所以需要刻画LCS的特征。 设A=“a0,a1,…,am”,B=“b0,b1,…,bn”,且Z=“z0,z1,…,zk”为它们的最长公共子序列。不难证明有以下性质: 如果am=bn,则zk=am=bn,且“z0,z1,…,z(k-1)”是“a0,a1,…,a(m-1)”和“b0,b1,…,b(n-1)”的一个最长公共子序列; 如果am!=bn,则若zk!=am,蕴涵“z0,z1,…,zk”是“a0,a1,…,a(m-1)”和“b0,b1,…,bn”的一个最长公共子序列; 如果am!=bn,则若zk!=bn,蕴涵“z0,z1,…,zk”是“a0,a1,…,am”和“b0,b1,…,b(n-1)”的一个最长公共子序列。
对应图解:
假如S1的最后一个元素与S2的最后一个元素相等,那么S1和S2的LCS就等于 {S1减去最后一个元素} 与 {S2减去最后一个元素} 的 LCS 再加上 S1和S2相等的最后一个元素。
假如S1的最后一个元素与S2的最后一个元素不等(本例子就是属于这种情况),那么S1和S2的LCS就等于 : {S1减去最后一个元素} 与 S2 的LCS, {S2减去最后一个元素} 与 S1 的LCS 中的最大的那个序列。
引进一个二维数组c[ ] [ ],用记录X[ i ]与Y[ j ]的LCS 的长度,b[ i ] [ j ]记录c[ i ] [ j ]是通过哪一个子问题的值求得的,以决定搜索的方向。 我们是自底向上进行递推计算,那么在计算c[i,j]之前,c[ i - 1 ] [ j - 1 ],c[ i - 1 ] [ j ]和c[ i ] [ j - 1 ]均已计算出来。此时我们根据X[ i ]==Y[ j ]还是X[ i ]!=Y[ j ],就可以计算出c[ i ] [ j ]。递推公式如下:

代码思路整合:
如下图,也正是由于在求解过程当中,有些步骤的结果会被反复使用,这也就是为什么使用动态规划建立表格,以空间换取时间的办法

建立二维数组及分析字符的比较情况

二维数组初始情况及转移方程(也就是填写记录表的情况)

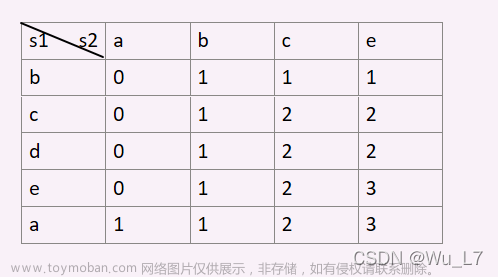
填写dp表格的两种情况:

dp表格填写过程说明:
如填写dp[2] [2]时,X[2-1] = b与Y[2-1] = c不相等,就是选择第二种情况,选择其左、上格子较大值填入,发现都是1,填入1;

如填写dp[3] [2]时,X[3-1] = c与Y[2-1] = c相等,就是选择第一种情况,选择其dp[i-1] [j-1]填入,发现是1,填入1+1=2;

最终结果:

代码:
#define Max 51//字符的最大个数
int m,n;
char a[m],b[n];//两个字符数组
int dp[Max][Max];//动态规划数组
char subs[Max];//存放LCS
void LCSLength()//求dp的过程
{
int i,j;
for (i = 0; i <= m; i++)//边界条件,将dp[i][0]也就是第一列全置为0
dp[i][0] = 0;
for (j = 0; j<= n; j++)//边界条件,将dp[0][j]也就是第一行全置为0
dp[0][j] = 0;
for (i = 1; i <= m; i++)//问题规模m*n
{
for (j = 1; j<= n; j++)
{
if (a[i-1] == b[j-1])//第一种情况,两个序列最后的一个字符相等
dp[i][j] = dp[i-1][j-1] + 1;
else//第二种情况,两个序列最后一个字符不相等
dp[i][j] = max(dp[i-1][j],dp[i][j-1]);//将该结点的左、上结点比较,将更大的值填入该结点
}
}
}那么到了这里我们只是填好了dp表格,但是我们要怎么样根据这个表格得到我们想要的LCS序列字符数组呢?
原理:由于我们填表的时候,当找到一个公共字符我们就会将dp[i] [j]的值设置为dp[i-1] [j-1] + 1的值,那么这个值也就是我们根据dp表找公共子序列的那个字符

寻找字符的过程:


最终情况:

回溯输出最长公共子序列过程:

对应代码:
void BuildSubs()
{
int k = dp[m][n];//填完了dp表之后,dp最右下角的那个数值就是子序列的最大长度
int i = m,j = n;
int len = 1;
while (k > 0)//子序列长度大于0时,在subs中放入最长公共子序列(反向)
{
if (dp[i][j] == dp[i-1][j])//与上方元素不相等,往上方回溯可能会遇见子序列
i--;
else if (dp[i][j] == dp[i][j-1])//与左方元素不相等,往左方回溯可能会遇见子序列
j--;
else//与上方、左给、方元素均不相等,即填表时X[i]==Y[j]遇见了子序列情况
{
subs[len++] = a[i-1];//subs中添加公共字符
i--;
j--;
k--;
}
}
}或者直接整合代码:
#include <stdio.h>
#include <string.h>
#define MAXLEN 51
void LCSLength(char *x, char *y, int m, int n, int c[][MAXLEN], int b[][MAXLEN])
{
int i, j;
for (i = 0; i <= m; i++)
c[i][0] = 0;
for (j = 1; j <= n; j++)
c[0][j] = 0;
for (i = 1; i <= m; i++)
{
for (j = 1; j <= n; j++)
{
if (x[i - 1] == y[j - 1])
{
c[i][j] = c[i - 1][j - 1] + 1;
b[i][j] = 0;//为了后面回溯,作为公共子序列的判定
}
else if (c[i - 1][j] >= c[i][j - 1])
{
c[i][j] = c[i - 1][j];
b[i][j] = 1;//为了后面向上回溯,向上寻找子序列的判定
}
else
{
c[i][j] = c[i][j - 1];
b[i][j] = -1;//为了后面向左回溯,向左寻找子序列的判定
}
}
}
}
void PrintLCS(int b[][MAXLEN], char *x, int i, int j)
{
if (i == 0 || j == 0)
return;
if (b[i][j] == 0)//找到了公共字符
{
PrintLCS(b, x, i - 1, j - 1);
printf("%c ", x[i - 1]);
}
else if (b[i][j] == 1)//向上回溯的过程
PrintLCS(b, x, i - 1, j);
else//向左回溯的过程
PrintLCS(b, x, i, j - 1);
}
int main(int argc, char **argv)
{
char x[MAXLEN] = { "ABCBDAB" };
char y[MAXLEN] = { "BDCABA" };
int b[MAXLEN][MAXLEN];
int c[MAXLEN][MAXLEN];
int m, n;
m = strlen(x);
n = strlen(y);
LCSLength(x, y, m, n, c, b);//填写动态规划表格
PrintLCS(b, x, m, n);//回溯输出最长公共子序列
return 0;
}部分文档参考:
BiliBili侠姐聊算法
程序员编程艺术第十一章:最长公共子序列(LCS)问题_v_JULY_v的博客-CSDN博客
部分图片引用:
(1条消息) 动态规划 最长公共子序列 过程图解_Running07的博客-CSDN博客_最长公共子序列文章来源:https://www.toymoban.com/news/detail-599423.html
鉴于个人见解整个代码以及动态规划的过程希望能帮助大家理解,制作不易文章来源地址https://www.toymoban.com/news/detail-599423.html
到了这里,关于最长公共子序列的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!