图论最短路径求解——手把手教你数学建模-Toy模板网

这篇具有很好参考价值的文章主要介绍了图论最短路径求解——手把手教你数学建模。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

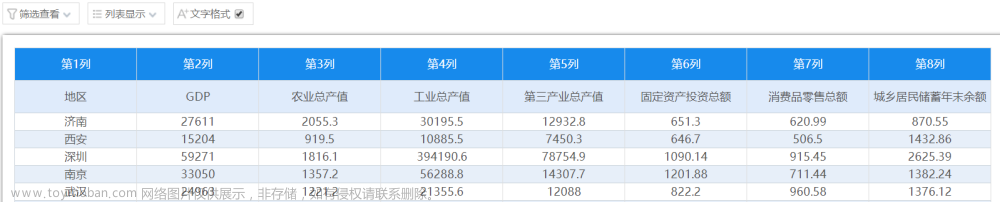
很多朋友在学习图论，或是数学建模的时候都会碰到最短路径问题。本讲将从如何作图开始，手把手教你图论中的最短路径问题。根据图的不同，我们将介绍两种不同的算法：迪杰斯特拉Dijkstra算法和Bellman‐Ford（贝尔曼‐福特）算法。

如何作图？

在线作图：https://csacademy.com/app/graph_editor/

MatLab作图：

% 函数graph(s,t)：可在 s 和 t 中的对应节点之间创建边，并生成一个图
G1 = graph(s1, t1);
plot(G1)  % plot函数用于MatLab中图的展示

% 函数graph(s,t,w)：可在 s 和 t 中的对应节点之间以w的权重创建边，并生成一个图
G2 = graph(s2, t2);
plot(G2, 'linewidth', 2)  % 设置线的宽度

% 下面的命令是在画图后不显示坐标
set( gca, 'XTick', [], 'YTick', [] ); 

% 有权重的图（如 s = [1,2,3,4]; t = [2,3,1,1]; w = [3,8,9,2]; ）
G3 = graph(s3, t3, w)
plot(G, 'EdgeLabel', G.Edges.Weight, 'linewidth', 2)  % 同时展示权重
set( gca, 'XTick', [], 'YTick', [] );

上面都是无向图，要做出有向图，只需要将graph改为digraph就行了。

注：Matlab做出来的图不是很漂亮，要是节点比较少，还是推荐使用在线作图

最短路径算法

迪杰斯特拉算法——贪心算法

原理：将节点分为是否访问的状态，每次增加已访问节点与未访问节点之间的最短路径。
使用范围：有向图、无向图。
缺点：不能处理负权重。

Bellman‐Ford（贝尔曼‐福特）算法

原理：利用循环来进行更新权重，且每循环一次，贝尔曼福特算法都会更新所有的节点的信息。（不再将节点区分为是否已访问的状态）
适用范围：支持带负权重的有向图，不支持含有负权回路的图。
缺点：运行时间较慢

Matlab函数求解

计算最短路径

[P,d] = shortestpath(G,start,end [,'Method',algorithm] )  %注意：该函数matlab2015b之后才有哦

功能：返回图G中start节点到end节点的最短路径

输入参数：
（1）G ‐ 输入图（graph 对象——无向图 | digraph 对象——有向图）
（2）start 起始的节点
（3）end 目标的节点
（4）[,‘Method’,algorithm]是可选的参数，表示计算最短路径的算法。一般我们不用手动设置，默认使用的是“auto”。MatLab会自动为我们匹配相应算法

输出参数：
（1）P – 最短路径经过的节点
（2）d – 最短距离

注：Matlab中的图节点要从1开始编号，所以要把0全部改为9

返回任意两点的距离矩阵

d = distances(G [,'Method',algorithm])  %注意：该函数matlab2015b之后才有哦

找给定范围内所有的点

[nodeIDs,dist] = nearest(G,s,d [,'Method',algorithm])  %注意：该函数matlab2016a之后才有哦

返回图形 G 中与节点 s 的距离在 d 之内的所有节点。
nodeIDs是符合条件的节点
Dist是这些节点与s的距离

来道例题

题目

下图为单行线交通网，每弧旁的数字表示通过这条线所需的费用。现在某人要从v1出发，通过这个交通网到v8去，求使总费用最小的旅行路线。
求源节点s到目标节点t的最短路径,数学建模,图论,matlab,算法,线性代数文章来源地址https://www.toymoban.com/news/detail-599462.html

题解

代码：

s = [1 1 1 2 3 3 4 5 5 5 5 6 6 7 9 9]; % 在 s 和 t 中的对应节点之间创建边
t = [2 3 4 5 2 4 6 4 6 7 8 5 7 8 5 8];
w = [6 3 1 1 2 2 10 6 4 3 6 10 2 4 2 3]; % 线路费用 —— 边的权重

G = digraph(s, t, w);  % 生成有向图
myplot = plot(G, 'EdgeLabel', G.Edges.Weight, 'linewidth', 2) % 通过MatLab画图
set( gca, 'XTick', [], 'YTick', [] );  % 画图后不显示坐标

[P,d] = shortestpath(G, 1, 8) % 求出最短路径（P）及其距离（d）
highlight(myplot, P, 'EdgeColor', 'r') % 高亮最短路径