图的存储结构
对于图结构而言,常见的存储结构主要有两种:邻接表和邻接矩阵:


邻接表很直观,我把每个节点
x的邻居都存到一个列表里,然后把x和这个列表关联起来,这样就可以通过一个节点x找到它的所有相邻节点。邻接矩阵则是一个二维布尔数组,我们权且称为
matrix,如果节点x和y是相连的,那么就把matrix[x][y]设为true(上图中绿色的方格代表true)。如果想找节点x的邻居,去扫一圈matrix[x][..]就行了。那么,为什么有这两种存储图的方式呢?肯定是因为他们各有优劣。
对于邻接表,好处是占用的空间少。
你看邻接矩阵里面空着那么多位置,肯定需要更多的存储空间。
但是,邻接表无法快速判断两个节点是否相邻。
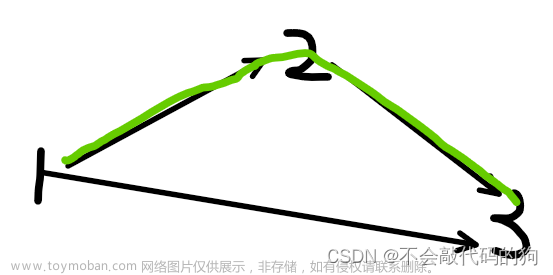
比如说我想判断节点
1是否和节点3相邻,我要去邻接表里1对应的邻居列表里查找3是否存在。但对于邻接矩阵就简单了,只要看看matrix[1][3]就知道了,效率高。所以说,使用哪一种方式实现图,要看具体情况。
图的遍历模板
在图论题目中,最常见的遍历方法是DFS,即深度优先遍历,图与二叉树不同,二叉树的遍历不会产生重复,但是图的遍历会产生重复,因此我们需要使用额外的存储空间来判断是否重复遍历该点,具体的深度优先遍历的遍历模板如下:
// 记录被遍历过的节点
boolean[] visited;
// 记录从起点到当前节点的路径
boolean[] onPath;
/* 图遍历框架 */
void traverse(Graph graph, int s) {
if (visited[s]) return;
// 经过节点 s,标记为已遍历
visited[s] = true;
// 做选择:标记节点 s 在路径上
onPath[s] = true;
for (int neighbor : graph.neighbors(s)) {
traverse(graph, neighbor);
}
// 撤销选择:节点 s 离开路径
onPath[s] = false;
}题目
题目描述
给定一个有 n 个节点的有向无环图,用二维数组 graph 表示,请找到所有从 0 到 n-1 的路径并输出(不要求按顺序)。
graph 的第 i 个数组中的单元都表示有向图中 i 号节点所能到达的下一些结点(译者注:有向图是有方向的,即规定了 a→b 你就不能从 b→a ),若为空,就是没有下一个节点了。
示例 1:
输入:graph = [[1,2],[3],[3],[]]
输出:[[0,1,3],[0,2,3]]
解释:有两条路径 0 -> 1 -> 3 和 0 -> 2 -> 3
示例 2:输入:graph = [[4,3,1],[3,2,4],[3],[4],[]]
输出:[[0,4],[0,3,4],[0,1,3,4],[0,1,2,3,4],[0,1,4]]
示例 3:输入:graph = [[1],[]]
输出:[[0,1]]
示例 4:输入:graph = [[1,2,3],[2],[3],[]]
输出:[[0,1,2,3],[0,2,3],[0,3]]
示例 5:输入:graph = [[1,3],[2],[3],[]]
输出:[[0,1,2,3],[0,3]]
提示:
n == graph.length
2 <= n <= 15
0 <= graph[i][j] < n
graph[i][j] != i
保证输入为有向无环图 (GAD)文章来源:https://www.toymoban.com/news/detail-601470.html
解题思路
由题意可得:graph[i]代表与i直接连接的元素,换句话说,graph实际上是在维护一张邻接表,题目中明确说明不存在环(结点不会相互指向),所以我们不需要设置visit[][]来判断是否访问过该结点,只需要按照dfs末班进行循环遍历,直到我们到达最后一个结点文章来源地址https://www.toymoban.com/news/detail-601470.html
实例代码
class Solution {
int size;
LinkedList<List<Integer>>res=new LinkedList<>();
LinkedList<Integer>path=new LinkedList<>();
public List<List<Integer>> allPathsSourceTarget(int[][] graph) {
size=graph.length;
path=new LinkedList<>();
dfs(graph,0);
return res;
}
public void dfs(int[][]graph,int index){
//添加
path.add(index);
//定义递归出口
if(index==size-1){
//添加最后一个元素
res.add(new LinkedList(path));
}
//循环
for(int i=0;i<graph[index].length;++i){
dfs(graph,graph[index][i]);
}
//删除
path.removeLast();
}
}到了这里,关于刷题日记09《图论基础》的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!