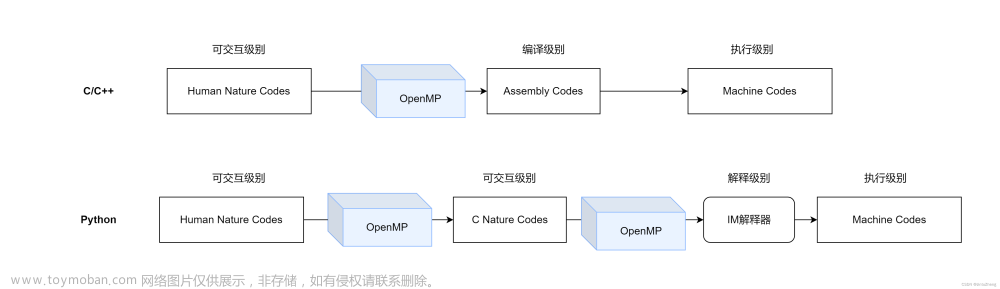
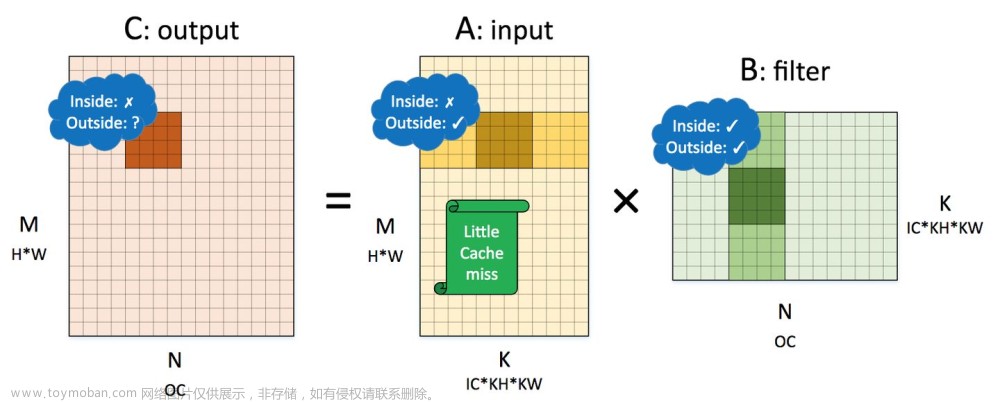
矩阵乘法优化的知名论文goto paper:
矩阵乘法的优化需要将矩阵切分成子矩阵,用子矩阵相乘的结果组合为原矩阵相乘的结果:

上图是拆分矩阵的方法,M表示矩阵,X方向和Y方向的两个维度都是未知的。P表示横条或竖条,X方向或Y方向有一个方向的维度是极小的。B表示block块,X方向和Y方向的两个维度都是极小的。
为了减小单个子矩阵计算量,要拆开A的整行和B的整列。不能让A的整行和B的整列作为子矩阵放入缓存进行计算。因此下图中第二列的Fig8和Fig10拆得最好,把A按列拆,使A的行不再完整,把B按行拆,使B的列不再完整。
下图是拆分矩阵后矩阵相乘的优化方法:

图中每列算法的含义:
第一列是 Matrix += Matrix * Matrix,就是矩阵乘加C += A * B。
第二列,(只讨论图8和图10,别的图不一样)是把 A 拆成多列、B 拆成多行,每次得到 与C尺寸相同的薄片,多层叠加得到完整的 C。
第三列是 更细致的拆分选择,A 的一列乘以 B 的一行,对于A 的一列乘以 B 的一行这一过程:
在第三列,Fig.8是把 A 的一列先拆成M个block,再将每个block(第i个)依次和 B 行相乘,相乘的结果是得到一个片(尺寸与C的子矩阵Ci相同),多个片叠加起来得到C矩阵;

在第三列,Fig.10是把 B 行拆成N个 block,再将每个block(第j个)依次被 A 乘,也是A列乘B行,得到C的一个片(尺寸与C的子矩阵Cj相同),再将C的多个片叠加得到C:

第四列和第三列的含义类似。
在第四列,Fig.8一个block乘以一行,共N个block。由于要放到register里,要减少数据的大小。必然行切成更小的slice;即把B竖着切成小块放进寄存器:

在第四列,Fig.10含义类似,把A横着切成小块放进寄存器。共M个block:

Fig.8在第四列处理竖着的小slice时,列主序是内存连续的,但行主序不连续。因此Fig.8更适合列主序。同理,此Fig.10更适合行主序。

因此最终结论是:列主序用Fig.8最优,因为竖着切;行主序用Fig.10最优,因为横着切。
对于Fig8的GEBP计算:

在如下 5 个前提都满足的情况下,理想的GEBP的计算过程和开销是怎么样的?
(前 3 个前提不考虑内存和寄存器存储结构中的 TLB,假设只有 内存、cache 和 ALU :)
- mc * kc 要小,小到 『 A + B的 nr 列 + C 的 nr 列 』能够一起塞进 cache
- 如果 1. 被满足,CPU 计算时不再受内存速度的限制,即得到的
gflops值就是真实的计算能力 - A 或 A 的分块只会被加载进 Cache 一次,
gemm过程中不会被换入又换出
(后 2 个前提要考虑 TLB,因为 TLB miss 会 stall CPU:)
4. mc 和 kc 要小,小到 『 A + B的 nr 列 + C 的 nr 列 』能够被 TLB 索引,即一定是小于 L2 cache 的。
5. A 或 A 的分块只被加载到 L2 cache 一次文章来源:https://www.toymoban.com/news/detail-601479.html
因为Fig.8用的就是GEBP,所以想要高性能(高gflops)就得满足上面 5 个前提。落到实处上就是如下4个参数限制,这些限制也是 OpenBLAS level3.c循环里写一堆if-else的理论根源:文章来源地址https://www.toymoban.com/news/detail-601479.html
- mc ≈ kc
- nr ≥ (Rcomp / 2 / Rload),其中 Rcomp 是算力、Rload 是 L2 cache 到 register 的带宽
- mc * kc ≤ K
- mc * kc 只能占 cache 的一半
到了这里,关于论文阅读:矩阵乘法GEMM的cache优化,子矩阵的切分方法Anatomy of High-Performance MatrixMultiplication的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!