线性代数——线性方程组

系列文章目录

• 学习高等数学和线性代数需要的初等数学知识
• 线性代数——行列式
• 线性代数——矩阵
• 线性代数——向量
• 线性代数——线性方程组
• 线性代数——特征值和特征向量
• 线性代数——二次型

版权声明

本文大部分内容皆来自李永乐老师考研教材和视频课。

线性方程组

方程组
$$\{\begin{array}{l}{a}_{11}{x}_1+a_{12}{x}_2+\cdots +a_{1n}{x}_n=b_1\\ a_{21}{x}_1+a_{22}{x}_2+\cdots +a_{2n}{x}_n=b_2\\ \dots \\ a_{m1}{x}_1+a_{m2}{x}_2+\cdots +a_{mn}{x}_n=b_m\end{array}\text{\hspace{1em}①}$$
称为$n$个未知数$m$个方程的非齐次线性方程组，如果$b_i=0(\forall i=1,2,\dots ,m)$，则方程组
$$\{\begin{array}{l}{a}_{11}{x}_1+a_{12}{x}_2+\cdots +a_{1n}{x}_n=0\\ a_{21}{x}_1+a_{22}{x}_2+\cdots +a_{2n}{x}_n=0\\ \dots \\ a_{m1}{x}_1+a_{m2}{x}_2+\cdots +a_{mn}{x}_n=0\end{array}\text{\hspace{1em}②}$$
称为齐次线性方程组，他是方程组①的导出组。若用一组数$c_1,c_2,\dots ,c_n$分别代替①中的$x_1,x_2,\dots ,x_n$，使①中$m$个等式都成立，则称有序组$c_1,c_2,\dots ,c_n$是①的一组解，解方程就是要找出方程组的全部解。如果①和②有相同的解集合，则称他们是同解方程组。方程组①的全体系数和常数项构成的矩阵
A ˉ = [ a 11 a 12 … a 1 n b 1 a 21 a 22 … a 2 n b 2 ⋮ ⋮ ⋮ ⋮ a m 1 a m 2 … a m n b m ] \bar{A}= \begin{bmatrix} a_{11}&a_{12}&\dots&a_{1n}&b_1\\ a_{21}&a_{22}&\dots&a_{2n}&b_2\\ \vdots&\vdots&&\vdots&\vdots\\ a_{m1}&a_{m2}&\dots&a_{mn}&b_m\\ \end{bmatrix} Aˉ= ​a11​a21​⋮am1​​a12​a22​⋮am2​​………​a1n​a2n​⋮amn​​b1​b2​⋮bm​​ ​
称为①的增广矩阵。由全体系数组成的矩阵
A = [ a 11 a 12 … a 1 n a 21 a 22 … a 2 n ⋮ ⋮ ⋮ a m 1 a m 2 … a m n ] A= \begin{bmatrix} a_{11}&a_{12}&\dots&a_{1n}\\ a_{21}&a_{22}&\dots&a_{2n}\\ \vdots&\vdots&&\vdots\\ a_{m1}&a_{m2}&\dots&a_{mn}\\ \end{bmatrix} A= ​a11​a21​⋮am1​​a12​a22​⋮am2​​………​a1n​a2n​⋮amn​​ ​
称为①的系数矩阵。方程组①和②可以分别表示为：
$$Ax=b\text{\hspace{1em}①}$$
$$Ax=0\text{\hspace{1em}②}$$
其中$x=(x_1,x_2,\dots ,x_n{)}^T,b=(b_1,b_2,\dots ,b_m{)}^T$。

有解判定定理

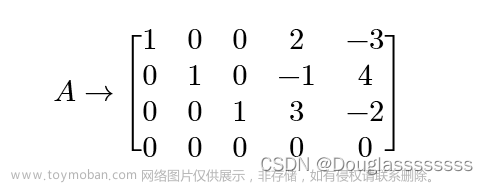
如果对$\bar{A}$进行初等行变换，得到行阶梯矩阵（这个过程叫做正向消元）
A ˉ = [ a 11 a 12 … a 1 n b 1 a 22 … a 2 n b 2 ⋱ ⋮ ⋮ 0 a r n b r 0 b r + 1 ⋮ ⋮ 0 0 ] \bar{A}= \begin{bmatrix} a_{11}&a_{12}&\dots&a_{1n}&b_1\\ &a_{22}&\dots&a_{2n}&b_2\\ &&\ddots&\vdots&\vdots\\ &&0&a_{rn}&b_r\\ &&&0&b_{r+1}\\ &&&\vdots&\vdots\\ &&&0&0 \end{bmatrix} Aˉ= ​a11​​a12​a22​​……⋱0​a1n​a2n​⋮arn​0⋮0​b1​b2​⋮br​br+1​⋮0​ ​
接着由下往上将化简后的矩阵加入未知数，即可得出线性方程的解（这个过程叫做反向求解），那么：

• 如果$b_{r+1}\ne 0$，则方程组①无解；
• 如果$b_{r+1}=0$，则方程组①有解，当$r=n$时有唯一解；当$r<n$时有无穷多解。

即：

• 方程组①有解的充要条件是$r(A)=r(\bar{A})$：
  • 若$r(A)=r(\bar{A})=n$，则方程组有唯一解；
  • 若$r(A)=r(\bar{A})<n$，则方程组有无穷多解；
• 方程组①无解$\iff r(A)+1=r(\bar{A})\iff b$不能由$A$的列向量线性表示。

同理，如果对$A$进行初等变换，得到行阶梯矩阵
A = [ a 11 a 12 … a 1 n a 22 … a 2 n ⋱ ⋮ 0 a r n 0 ⋮ 0 ] A= \begin{bmatrix} a_{11}&a_{12}&\dots&a_{1n}\\ &a_{22}&\dots&a_{2n}\\ &&\ddots&\vdots\\ &&0&a_{rn}\\ &&&0\\ &&&\vdots\\ &&&0 \end{bmatrix} A= ​a11​​a12​a22​​……⋱0​a1n​a2n​⋮arn​0⋮0​ ​
那么：

• 如果$a_{rn}\ne 0$，则方程组②只有零解；
• 如果$a_{rn}=0$，则方程组②有解，且有无穷多解。

即：方程组②有非零解$\iff r(A)<n\iff A$的列向量线性相关。

齐次线性方程组的基础解系

如果向量组${\eta }_1,{\eta }_2,\dots ,{\eta }_t$满足：

• ${\eta }_1,{\eta }_2,\dots ,{\eta }_t$是②的解；
• ${\eta }_1,{\eta }_2,\dots ,{\eta }_t$线性无关；
• ②的任意一个解都能由${\eta }_1,{\eta }_2,\dots ,{\eta }_t$线性表出。

则称${\eta }_1,{\eta }_2,\dots ,{\eta }_t$为齐次线性方程组②的基础解系，那么对任意常数$c_1,c_2,\dots ,c_t$
$$c_1{\eta }_1+c_2{\eta }_2+\cdots +c_t{\eta }_t$$
是齐次方程组②的通解。齐次线性方程组解的性质如下：

• 如果${\eta }_1,{\eta }_2$是方程组②的两个解，那么其线性组合仍是②的解。
  证明：
  $$\begin{gathered} \because A{\eta }_1=0,A{\eta }_2=0 \\ \therefore A(k{\eta }_1+l{\eta }_2)=kA{\eta }_1+lA{\eta }_2=0 \end{gathered}$$
• 若$r(A)=r<n$，则②有$n-r$个线性无关的解，且②的任何一个解都可这由$n-r$个线性无关的解线性表示。
  证明：设$A$的前$r$个列向量线性无关，对$A$进行初等行变换化为行阶梯矩阵：
  A = [ 1 0 … a 1 r + 1 … a 1 n 1 … a 2 r + 1 … a 2 n ⋱ ⋮ ⋮ ⋮ a r r + 1 … a r n 0 … 0 0 … 0 ] A= \begin{bmatrix} 1&0&\dots&a_{1r+1}&\dots&a_{1n}\\ &1&\dots&a_{2r+1}&\dots&a_{2n}\\ &&\ddots&\vdots&\vdots&\vdots\\ &&&a_{rr+1}&\dots&a_{rn}\\ &&&0&\dots&0\\ &&&0&\dots&0\\ \end{bmatrix} A= ​1​01​……⋱​a1r+1​a2r+1​⋮arr+1​00​……⋮………​a1n​a2n​⋮arn​00​ ​
  那么可得方程组：
  $$\{\begin{array}{l}{x}_1=c_{1r+1}{x}_{r+1}-\cdots -c_{1n}{x}_n\\ x_2=c_{2r+1}{x}_{r+1}-\cdots -c_{2n}{x}_n\\ \dots \\ x_r=c_{rr+1}{x}_{rr+1}-\cdots -c_{rn}{x}_n\end{array}$$
  令
  [ x r + 1 x r + 2 ⋮ x n ] \begin{bmatrix} x_{r+1}\\ x_{r+2}\\ \vdots\\ x_{n} \end{bmatrix} ​xr+1​xr+2​⋮xn​​ ​
  分别是
  [ 1 0 ⋮ 0 ] [ 0 1 ⋮ 0 ] … [ 0 0 ⋮ 1 ] \begin{bmatrix} 1\\ 0\\ \vdots\\ 0 \end{bmatrix} \begin{bmatrix} 0\\ 1\\ \vdots\\ 0 \end{bmatrix} \dots \begin{bmatrix} 0\\ 0\\ \vdots\\ 1 \end{bmatrix} ​10⋮0​ ​ ​01⋮0​ ​… ​00⋮1​ ​
  代入方程组得②的$n-r$个解：
  η 1 = [ − c 1 r + 1 ⋮ − c r r + 1 1 0 ⋮ 0 ] η 2 = [ − c 1 r + 2 ⋮ − c r r + 2 0 1 ⋮ 0 ] … η n − r = [ − c 1 n ⋮ − c r n 0 0 ⋮ 1 ] \eta_1=\begin{bmatrix} -c_{1r+1}\\ \vdots\\ -c_{rr+1}\\ 1\\ 0\\ \vdots\\ 0 \end{bmatrix} \eta_2=\begin{bmatrix} -c_{1r+2}\\ \vdots\\ -c_{rr+2}\\ 0\\ 1\\ \vdots\\ 0 \end{bmatrix} \dots \eta_{n-r}=\begin{bmatrix} -c_{1n}\\ \vdots\\ -c_{rn}\\ 0\\ 0\\ \vdots\\ 1 \end{bmatrix} η1​= ​−c1r+1​⋮−crr+1​10⋮0​ ​η2​= ​−c1r+2​⋮−crr+2​01⋮0​ ​…ηn−r​= ​−c1n​⋮−crn​00⋮1​ ​
  因为$(1,0,\dots ,0{)}^T,(0,1,\dots ,0{)}^T,(0,0,\dots ,1{)}^T$线性无关，所以${\eta }_1,{\eta }_2,\dots ,{\eta }_{n-r}$线性无关。设$$\eta =(d_1,d_2,\dots ,d_n{)}^T$$是②的任一解，则：
  $$\gamma =d_{r+1}{\eta }_1+d_{r+2}{\eta }_2+\cdots +d_n{\eta }_{n-r}-\eta =(l_1,l_2,\dots .l_r,0,0,\dots ,0{)}^T$$
  必为②的一个解，带入②得：
  $$l_1=0,l_2=0,\dots ,l_r=0$$
  即$\gamma =0$，所以
  $$\eta =d_{r+1}{\eta }_1+d_{r+2}{\eta }_2+\cdots +d_n{\eta }_{n-r}$$
  因此②的任何一个解都可这由$n-r$个线性无关的解线性表示。

非齐次线性方程组解的结构

对方程组①，若$r(A)=r(\bar{A})=r$，且已知${\eta }_1,{\eta }_2,\dots ,{\eta }_{n-r}$是②的基础解系，${\xi }_0$是①的某个已知解，则①的通解为：
$${\xi }_0+c_1{\eta }_1+c_2{\eta }_2+\cdots +c_{n-r}{\eta }_{n-r}$$
其中$c_1,c_2,\dots ,c_{n-r}$为任意常数。非齐次线性方程组解的性质如下：

• 如果$\alpha ,\beta$是①的两个解，那么$\alpha -\beta$是②的解。
  证明：
  $$\begin{gathered} \because A\alpha =b,A\beta =b \\ \therefore A(\alpha -\beta )=0 \end{gathered}$$
• 如果$\alpha$是①的解，$\eta$是②的解，则$\alpha +\eta$是①的解。
  证明：
  $$\begin{gathered} \because A\alpha =b,A\eta =0 \\ \therefore A(\alpha +k\eta )=A\alpha +kA\eta =b+0=b \end{gathered}$$

公共解

如果已知两个方程组Ⅰ和Ⅱ，欲求其公共解，那么有以下三个方法：

• 将其联立$\{\begin{array}{l}Ⅰ\\ Ⅱ\end{array}$，联立方程组的通解就是Ⅰ和Ⅱ的公共解。
• 如果已知Ⅰ和Ⅱ的基础解系分别是${\alpha }_1,{\alpha }_2$和${\beta }_1,{\beta }_2$，那么可设公共解为$\gamma$，则
  $$\gamma =k_1{\alpha }_1+k_2{\alpha }_2=l_1{\beta }_1+l_2{\beta }_2$$
  两式相减联立方程组解出系数即可求得公共解$\gamma$。
• 如果已知Ⅰ的通解为$k_1{\alpha }_1+k_2{\alpha }_2$，就将其带入到Ⅱ，如果仍是Ⅱ的解，那么求出$k_1,k_2$满足的关系式从而求出通解。

两方程组解的关系

• $Ax=0$的解是$BAx=O$的解
• 如果$Ax=O$的解是$Bx=O$的解，则$B$的行向量可由$A$的行向量线性表示。
• 如果$Ax=O$的解是$Bx=O$的解，$Bx=O$的解是$Ax=O$的解，则$Ax=O$、$Bx=O$同解。
  • 两个方程组同解$\iff$系数矩阵行向量组等价
  • $A^{T}Ax=O$和$Ax=O$同解

克拉默法则

若$n$个未知数、$n$个方程的线性方程组：$$\{\begin{array}{l}{a}_{11}{x}_1+a_{12}{x}_2+\cdots +a_{1n}{x}_n=b_1\\ a_{21}{x}_1+a_{22}{x}_2+\cdots +a_{2n}{x}_n=b_2\\ \dots \\ a_{n1}{x}_1+a_{n2}{x}_2+\cdots +a_{nn}{x}_n=b_n\end{array}$$的系数行列式： D = ∣ a 11 a 12 … a 1 n a 21 a 22 … a 2 n ⋮ ⋮ ⋮ a n 1 a n 2 … a n n ∣ ≠ 0 D=\begin{vmatrix}a_{11}&a_{12}&\dots&a_{1n}\\a_{21}&a_{22}&\dots&a_{2n}\\\vdots&\vdots&&\vdots\\a_{n1}&a_{n2}&\dots&a_{nn}\end{vmatrix}≠0 D= ​a11​a21​⋮an1​​a12​a22​⋮an2​​………​a1n​a2n​⋮ann​​ ​=0则方程组有唯一解：$$x_1=\frac{D_1}{D},x_2=\frac{D_2}{D},\dots ,x_n=\frac{D_n}{D}$$其中 D j = ∑ i = 1 n b i A i j = ∣ a 11 … a 1 , j − 1 b 1 a 1 , j + 1 … a 1 n a 21 … a 2 , j − 1 b 2 a 2 , j + 1 … a 2 n ⋮ ⋮ ⋮ ⋮ ⋮ a n 1 … a n , j − 1 b n a n , j + 1 … a n n ∣ ( j = 1 , 2 , … , n ) D_j=\sum_{i=1}^nb_iA_{ij}=\begin{vmatrix}a_{11}&\dots&a_{1,j-1}&b_1&a_{1,j+1}&\dots&a_{1n}\\a_{21}&\dots&a_{2,j-1}&b_2&a_{2,j+1}&\dots&a_{2n}\\\vdots&&\vdots&\vdots&\vdots&&\vdots\\a_{n1}&\dots&a_{n,j-1}&b_n&a_{n,j+1}&\dots&a_{nn}\end{vmatrix}(j=1,2,\dots,n) Dj​=i=1∑n​bi​Aij​= ​a11​a21​⋮an1​​………​a1,j−1​a2,j−1​⋮an,j−1​​b1​b2​⋮bn​​a1,j+1​a2,j+1​⋮an,j+1​​………​a1n​a2n​⋮ann​​ ​(j=1,2,…,n)
若齐次方程组：$$\{\begin{array}{l}{a}_{11}{x}_1+a_{12}{x}_2+\cdots +a_{1n}{x}_n=0\\ a_{21}{x}_1+a_{22}{x}_2+\cdots +a_{2n}{x}_n=0\\ \dots \\ a_{n1}{x}_1+a_{n2}{x}_2+\cdots +a_{nn}{x}_n=0\end{array}$$的系数行列式$D\ne 0$，则方程组只有零解。若有非零解，则系数行列式$D=0$。文章来源地址https://www.toymoban.com/news/detail-601811.html

到了这里，关于线性代数——线性方程组的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！