Particle Swarm Optimization
粒子群算法(PSO算法)
定义
粒子群算法,又称粒子群优化算法(Particle Swarm Optimization),缩写为 PSO, 是近年来发展起来的一种新的进化算法(Evolutionary Algorithm - EA),由Eberhart 博士和Kennedy 博士于1995年提出,其源于对鸟群捕食的行为研究。
算法思想
PSO模拟鸟群的捕食行为。
设想这样一个场景:一群鸟在随机搜索食物,在这个区域里只有一块食物,所有的鸟都不知道食物在那里,但是它们知道当前的位置离食物还有多远,那么找到食物的最优策略是什么呢?
最简单有效的就是搜寻目前离食物最近的鸟的周围区域。都向这片区域靠拢。
抽象
PSO中,将问题的搜索空间类比于鸟类的飞行空间,将每只鸟抽象为一个无质量无体积的微粒,用以表征优化问题的一个候选解,我们称之为“粒子”,优化所需要寻找的最优解则等同于要寻找的食物。
所有的粒子都有一个由被优化的函数决定的适应值(fitness value),每个粒子还有一个速度决定他们飞翔的方向和距离,然后粒子们就追随当前的最优粒子在解空间中搜索。
PSO初始化为一群随机粒子(随机解、一群鸟),然后通过迭代找到最优解。在每一次迭代中,粒子(鸟)通过跟踪两个“极值”来更新自己的位置。一个就是粒子本身所找到的最优解,这个解叫做个体极值pBest,另一个极值是整个种群目前找到的最优解,这个极值是全局极值gBest。(gBest是pBest中最好值)
算法介绍
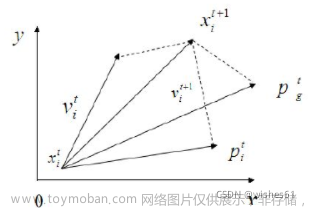
•在找到这两个最优值时,粒子根据如下的公式来更新自己的速度和位置:
V
=
w
×
V
+
c
1
×
r
a
n
d
(
)
×
(
p
B
e
s
t
−
P
r
e
s
e
n
t
)
+
c
2
×
r
a
n
d
(
)
×
(
g
B
e
s
t
−
P
r
e
s
e
n
t
)
P
r
e
s
e
n
t
=
P
r
e
s
e
n
t
+
V
V = w \times V \\ \qquad + c_1 \times rand() \times ( pBest - Present ) \\ \qquad + c_2 \times rand() \times ( gBest - Present ) \\ Present = Present + V
V=w×V+c1×rand()×(pBest−Present)+c2×rand()×(gBest−Present)Present=Present+V
- V 是例子速度 velocity
- Present 是粒子当前位置
- pBest 个体极值 最优解
- gBest 全局极值 最优解
- rand() 是(0,1)之间的随机数
- c_1、c_2 是学习因子 使粒子具有自我总结和向群体中优秀个体学习的能力,从而向群体内或邻域内最优点靠近,c_1和 c_2 通常等于2,并且范围在 0 和 4 之间
- w 是加权系数(惯性权重)决定了对粒子当前速度继承多少,合适的选择可以使粒子具有均衡的探索能力和开发能力,惯性权重的取法有常数法、线性递减法、自适应法等。
- Vmax: 最大速度,决定粒子在一个循环中最大的移动距离, 通常设定为粒子的范围宽度,例如,粒子 (x1, x2, x3) ,x1 属于 [-10, 10], 那么 x1的Vmax 的大小就是 20。
- 粒子数(鸟的个数): 一般取 1~40. 其实对于大部分的问题10个粒子已经足够可以取得好的结果;
- 粒子的长度(维度): 这是由优化问题决定, 就是问题解的长度(决策变量个数);
- 粒子的范围: 由优化问题决定,每一维可以设定不同的范围;
- 中止条件: 最大循环数以及最小错误要求。
将粒子延伸到N维空间,粒子i在N维空间里的位置表示为一个矢量,每个粒子的飞行速度也表示为一个矢量。
举例
对于问题 f(x) = x1^2 + x22+x32 求解,粒子可以直接编码为 (x1, x2, x3),而适应度函数就是f(x),接着我们就可以利用前面的过程去寻优,寻优过程是一个迭代过程, 中止条件一般为设置为达到最大循环数或者最小错误要求。

例题
找下式的极大值
f
(
x
,
y
)
=
s
i
n
x
2
+
y
2
x
2
+
y
2
+
e
c
o
s
2
π
x
+
c
o
s
2
π
y
2
−
2.71289
f(x,y)=\frac{sin\sqrt{x^2+y^2}}{\sqrt{x^2+y^2}}+e^{\frac{cos2\pi x+cos2\pi y}{2}}-2.71289
f(x,y)=x2+y2sinx2+y2+e2cos2πx+cos2πy−2.71289
这里我们使用的工具是Python,我将从头到尾演示一下这整个过程
导入需要用的包
import random
import numpy as np
import math
import matplotlib.pyplot as plt
初始化粒子以及例子速度
这里我们选用了20个粒子,把粒子的x和y初始化在[-2,2]上,活动范围也都是[-2,2],速度都是0,v_max设置为[10,10]
pBest我用来记录fitness value最大的位置,所以我先使pBest = particles,gBest 在这里取第一个pBest的值,如果一次迭代都没有的话那就会出错。
fxyRecord 用来记录每一轮迭代的fitness value的最大值,indexBest用来记录当前使fitness value最大的那个粒子的index
c1和c2学习因子都选用了2,w惯性权重选用了0.8
number_of_particles = 20
particles = np.random.rand(number_of_particles*2)*2
particles=particles.reshape((number_of_particles,2))
rangeParticle = np.array([[-2,2],[-2,2]])
velocities = np.zeros((number_of_particles, 2))
v_max = np.array([10,10])
pBest = particles.copy()
gBest = pBest[0]
fxyRecord = np.array([])
indexBest = 0
c1 = 2
c2 = 2
w = 0.8
epoch = 0
粒子适应度检测
首先我们要给出fitness value的计算函数
def f(x,y):
sqrtx2plusy2 =math.sqrt(math.pow(x,2)+math.pow(y,2))
firstTerm = math.sin(sqrtx2plusy2)/sqrtx2plusy2
secondTerm = math.exp((math.cos(2*math.pi*x) + math.cos(2*math.pi*y))/2)
return firstTerm+secondTerm-2.71289
让每个粒子都计算出他当前的fitness value,并即使更新pBest和gBest,并用fxyRecord和indexBest记录其结果。
for index in range(number_of_particles):
present = particles[index]
x = present[0]
y = present[1]
fxy=f(x,y)
if f(pBest[index][0],pBest[index][1]) < fxy:
pBest[index] = np.array([x,y])
if f(gBest[0],gBest[1]) < fxy:
gBest =np.array([x,y])
indexBest = index
fxyRecord=np.append(fxyRecord,f(gBest[0],gBest[1]))
粒子速度位置更新
根据当前的V、当前的位置(present)、pBest、gBest以及公式计算出下一个V,记得限制V的大小,然后保存这个计算出来的V作为当前的V
根据计算出的V 计算出下一个位置,同样需要限制粒子位置的范围(如果粒子的某个维度如果超过了range,在这里我设置这个粒子的这个维度的位置为被超过的这个range的值,这里其实还有各种各样的方案,比如反弹什么的,这个可以加入很多自己的畅想),然后保存这个计算出来的位置作为当前的位置
for index in range(number_of_particles):
present = particles[index]
x = present[0]
y = present[1]
V = w*velocities[index] + c1*random.random()*(pBest[index]-present)+c2*random.random()*(gBest-present)
# limit velocity
if V[0]<v_max[0]*-1/2:
V[0]=v_max[0]*-1/2
elif V[0]>v_max[0]*1/2:
V[0]=v_max[0]*1/2
if V[1]<v_max[1]*-1/2:
V[1]=v_max[1]*-1/2
elif V[1]>v_max[1]*1/2:
V[1]=v_max[1]*1/2
velocities[index]=V
particles[index]=present+V
# limit coordinates
if particles[index][0]<rangeParticle[0][0]:
particles[index][0]=rangeParticle[0][0]
elif particles[index][0]>rangeParticle[0][1]:
particles[index][0]=rangeParticle[0][1]
if particles[index][1]<rangeParticle[1][0]:
particles[index][1]=rangeParticle[1][0]
elif particles[index][1]>rangeParticle[1][1]:
particles[index][1]=rangeParticle[1][1]
可视化
我通过绘制出粒子的位置以及迭代次数与fitness value对应的diagram来表现这个算法,使其相对直观一些,函数如下
def show(epoch):
fig = plt.figure(figsize=(9,4))
columns = 2
rows = 1
fig.add_subplot(rows, columns, 2)
x_major_locator=plt.MultipleLocator(math.floor(epoch/10)+1)
ax=plt.gca()
ax.xaxis.set_major_locator(x_major_locator)
plt.plot(fxyRecord)
fig.add_subplot(rows, columns, 1)
plt.xlim(np.array(gBest[0]+rangeParticle[0]/(epoch+1)))
plt.ylim(np.array(gBest[1]+rangeParticle[1]/(epoch+1)))
plt.scatter(particles.T[0],particles.T[1],s=10)
plt.scatter(gBest[0],gBest[1],c='r',s=15)
尝试一下可视化
show(epoch)
epoch+=1
print(f"第{epoch}轮 极大值为:{f(gBest[0],gBest[1])} 对应粒子index:{indexBest} x:{gBest[0]} y:{gBest[1]}")

多运行几轮,逐一观察






可见该算法还是相对容易陷入局部最优的问题,最好还是结合其他算法,来避免这个问题。
经过多次实验可以得到以下结果文章来源:https://www.toymoban.com/news/detail-601905.html
 文章来源地址https://www.toymoban.com/news/detail-601905.html
文章来源地址https://www.toymoban.com/news/detail-601905.html
到了这里,关于Particle Swarm Optimization粒子群优化算法(PSO算法)概念及实战的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!