理论概述
定义
图(Graph)是由节点(Vertex)和连接节点的边(Edge)组成的一种非线性数
据结构。它用于描述事物之间的关系、连接或依赖。图是一种非线性的数据结构,
它广泛应用于计算机科学、数学、工程等领域。

基本概念
节点(Node):也称为顶点(Vertex),表示图中的一个对象或实体。节点可以
代表人、地点、物体或抽象概念等。节点可以有属性和标签。
边(Edge):也称为连接(Link)或关系(Relation),表示节点之间的连接
或相互关系。边可以是有向或无向的,有向边有一个起点和一个终点,无向边表
示双向关系。
加权图(Weighted Graph):图中的边可以带有权重或成本,表示两个节点之
间的距离、耗费或其他度量。
路径(Path):图中的路径是由一系列边连接的节点序列。路径的长度可以通过
边的数量或边上的权重来衡量。
入度(In-degree)和出度(Out-degree):在有向图中,每个节点有一个入度
(指向该节点的边的数量)和一个出度(从该节点发出的边的数量)。

图的类型
加权图(Weighted Graph):图中的边带有权重或成本,表示节点之间的距离、
耗费或其他度量。权重可以是实数、整数或其他类型的值。
无权图(Unweighted Graph):图中的边没有权重,只表示节点之间的连接关
系,不考虑边的权重值。
完全图(Complete Graph):在无向图中,任意两个节点之间都有边相连,形
成完全图。具有n个节点的完全图有n(n-1)/2条边。
稀疏图和稠密图(Sparse Graph and Dense Graph):稀疏图指的是边的数量
相对较少的图,而稠密图指的是边的数量相对较多的图。
有环图和无环图(Cyclic Graph and Acyclic Graph):有环图包含至少一个
环(循环)的图,即可以沿着边形成一个回路。无环图没有任何环。
连通图和非连通图(Connected Graph and Disconnected Graph):连通图
指的是图中任意两个节点之间都存在路径的图,非连通图则存在节点不可达的情
况。可以把非连通图划分为多个连通子图。
强连通图和弱连通图(Strongly Connected Graph and Weakly Connected
Graph):强连通图是有向图中,任意两个节点之间都存在双向路径的图。弱连
通图是在将有向图中的边的方向忽略后形成的连通图。
生成树(Spanning Tree):生成树是一个无环连通子图,包含了原图中所有节
点,并且通过最少的边连接这些节点。

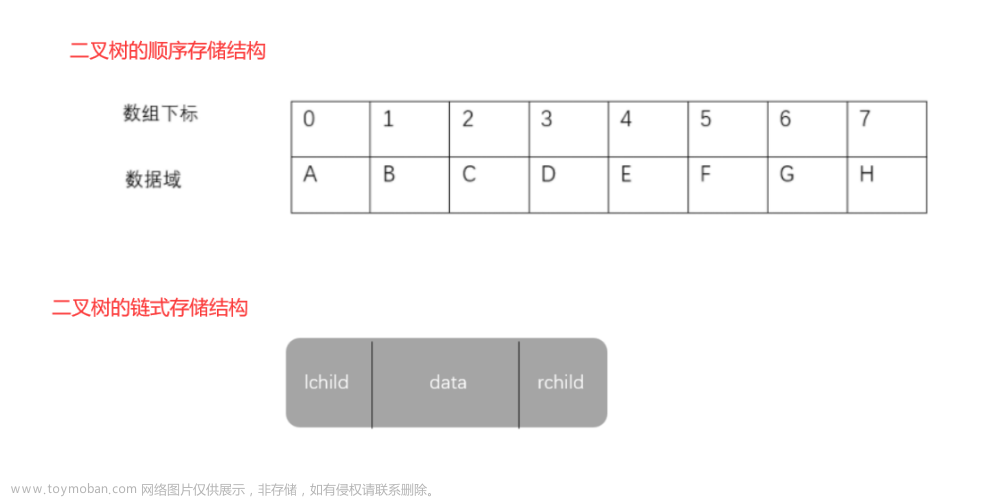
表示方法
邻接矩阵(Adjacency Matrix):
邻接矩阵是一个二维数组,用于表示图中节点之间的连接关系。矩阵的行和列分
别对应图中的节点,在相应的位置上使用0或1表示节点之间是否有边相连。如果
是加权图,则可以使用权重值来代替1。

优点:
邻接矩阵易于理解和实现。
可以快速查找节点之间是否有边相连,时间复杂度为O(1)。
适用于稠密图。
缺点:
对于大规模的稀疏图,邻接矩阵会占用较大的存储空间。
插入和删除边的操作比较耗时,时间复杂度为O(1)。
邻接表(Adjacency List):
邻接表是一种链表数组的形式,用于表示图中每个节点的邻接节点。每个节点都
有一个链表,链表中存储着与该节点相连的其他节点。
优点:
邻接表表示方法可以有效地表示稀疏图,节省存储空间。
插入和删除边的操作效率较高,时间复杂度为O(1)。
适用于大多数实际应用中的图结构。
缺点:
查找节点之间是否有边相连的操作较慢,时间复杂度为O(V),其中V是节点的数
量。
无法直接获取节点的入度和出度。
关联矩阵(Incidence Matrix):
关联矩阵是一个二维数组,用于表示图中的节点和边之间的关联关系。矩阵的行
表示节点,列表示边,当节点与边相连时,相应的位置上使用1表示。
优点:
可以表示多重图,即允许同一对节点之间存在多条边的图。
可以通过统计列向量或行向量来获取节点的入度和出度。
缺点:
占用较大的存储空间。
无法直接获取节点之间的连接关系。
其他表示方法:
邻接集合(Adjacency Set):使用集合来表示每个节点与其邻居节点之间的连
接关系。
邻接字典(Adjacency Dictionary):使用字典来表示每个节点与其邻居节点
之间的连接关系。
 文章来源:https://www.toymoban.com/news/detail-603127.html
文章来源:https://www.toymoban.com/news/detail-603127.html
应用场景
图在各个领域都有广泛的应用,以下是一些常见的图应用以及它们的详细介绍:
1、社交网络分析:
社交网络分析是对社交网络结构和社交行为进行建模和分析的过程。通过将社交
关系表示为图,可以研究网络的特征、社区发现、信息传播、影响力分析等。社
交网络分析在社交媒体、营销、社会学等领域具有重要意义。
2、路由和通信网络:
图在路由和通信网络中起着核心作用。将网络设备和连接表示为图中的节点和边,
可以分析网络的拓扑结构和性能特征,开发高效的路由算法,以实现快速且可靠
的数据传输和通信。
3、推荐系统:
基于图的推荐系统利用用户和物品的关系构建推荐图。通过分析图中的节点和边,
推荐系统可以识别用户的兴趣、发现相似物品或用户,从而向用户提供个性化的
推荐。这在电子商务、社交媒体和内容推荐中具有重要作用。
4、地图和导航系统:
图在地图和导航系统中被广泛使用。将道路、地理位置和交通网络表示为图,可
以应用最短路径算法来实现导航和路径规划。这对于交通管理、智能交通系统和
导航应用至关重要。
5、数据库和知识图谱:
图数据库和知识图谱使用图来存储实体(节点)和它们之间的关系(边)。通过
图的查询和分析,可以揭示实体之间的复杂关系,支持数据探索、问题解决和知
识发现。这对于知识图谱、智能推理和大数据分析非常关键。
6、组织结构和关系分析:
将组织结构、业务流程和关系网络表示为图,可以揭示组织内部的关系、层次结
构和流程,辅助决策制定、流程优化和组织管理。这在组织学、人力资源管理和
流程改进中具有重要意义。
7、生物网络和蛋白质相互作用:
图在生物学中用于表示基因、蛋白质和它们之间的相互作用关系。通过分析生物
网络的拓扑结构和功能特征,可以理解生物体内的调控机制、疾病发展和药物研
发。这对于系统生物学和药物研究非常重要。
8、可视化和图形表示:
图可用于可视化和图形表示数据。通过将数据表示为节点和边的形式,可以创建
图形图表和网络图,直观地展示数据的关系和模式。这对于数据可视化、信息图
表和交互性数据探索非常有用。
补充
这些应用只是图在不同领域中的一些例子。图的应用范围非常广泛,为我们理解
和解决复杂问题提供了强大的工具和方法。
注意事项
数据预处理: 在应用图之前,需要对原始数据进行预处理。这包括数据清洗、去
除噪声、处理缺失数据和异常值等。预处理步骤可以提高数据的质量,减少后续
分析的偏差和误差。
图的表示方式选择: 根据具体问题和应用场景,选择合适的图表示方式。邻接矩
阵适用于稠密图,邻接表适用于稀疏图,关联矩阵适用于多重图,而邻接集合或
邻接字典适用于特定的操作和查询需求。
图的存储和计算效率: 图的存储和计算效率是处理大规模图的关键因素。使用合
适的数据结构和算法可以减少存储空间和计算复杂性。例如,压缩存储技术可以
有效减少稀疏图的存储空间。
并行和分布式处理: 对于大规模图数据,采用并行计算或分布式处理方法可以
显著提高处理速度和计算能力。这包括使用并行算法、分布式图处理框架和分
布式存储系统等。
图算法的选择和调优: 不同的图算法适用于不同的问题和场景。在选择算法时,
要考虑算法的时间复杂性、空间复杂性、精度和可扩展性。有时需要对算法进
行调优和参数调节,以满足特定需求。
可视化的交互性和表达力: 当使用图进行可视化时,要关注图的交互性和表达
力。交互性可以帮助用户探索和发现图中的模式和关系,而表达力则要求选择
合适的视觉编码和布局算法,以清晰、准确地呈现数据。
基准测试和验证: 在应用图算法和技术时,进行基准测试和验证非常重要。通过
比较不同算法的性能、结果和准确性,可以评估其优劣并选择最适合的算法。
此外,需要针对具体问题进行验证和验证结果的可信性。
隐私和安全性: 如果图数据涉及敏感信息,应考虑隐私和安全性问题。确保对图
数据进行适当的加密、脱敏和访问控制,以防止未经授权的访问和数据泄露。
不同图算法的特性: 不同的图算法有不同的特性和适用范围。有些算法适用于全
局图分析,如图遍历和图搜索算法;有些算法适用于局部图分析,如图聚类和图
中心性算
 文章来源地址https://www.toymoban.com/news/detail-603127.html
文章来源地址https://www.toymoban.com/news/detail-603127.html
代码实现
该代码包括图的创建、添加边、获取邻居节点等基本操作:
import java.util.ArrayList;
import java.util.HashMap;
import java.util.List;
import java.util.Map;
class Graph {
private Map<Integer, List<Integer>> adjacencyList;
// 构造函数,初始化图
Graph() {
adjacencyList = new HashMap<>();
}
// 添加节点到图
void addVertex(int vertex) {
adjacencyList.put(vertex, new ArrayList<>());
}
// 添加边到图
void addEdge(int source, int destination) {
if (!adjacencyList.containsKey(source) || !adjacencyList.containsKey(destination)) {
throw new IllegalArgumentException("节点不存在");
}
adjacencyList.get(source).add(destination);
adjacencyList.get(destination).add(source);
}
// 获取邻居节点列表
List<Integer> getNeighbors(int vertex) {
if (!adjacencyList.containsKey(vertex)) {
throw new IllegalArgumentException("节点不存在");
}
return adjacencyList.get(vertex);
}
}
public class Main {
public static void main(String[] args) {
Graph graph = new Graph();
// 添加节点到图
graph.addVertex(0);
graph.addVertex(1);
graph.addVertex(2);
graph.addVertex(3);
// 添加边到图
graph.addEdge(0, 1);
graph.addEdge(0, 2);
graph.addEdge(1, 2);
graph.addEdge(2, 3);
// 获取节点的邻居节点列表
List<Integer> neighbors = graph.getNeighbors(2);
System.out.println("节点2的邻居节点列表:" + neighbors);
}
}
下面展示了如何使用邻接表来表示图,并实现了广度优先搜索(BFS)和深度优先搜索(DFS)算法。
import java.util.*;
class Graph {
private int V; // 图中节点的数量
private LinkedList<Integer> adjList[]; // 邻接表表示边的列表
// 构造函数,初始化图
Graph(int v) {
V = v;
adjList = new LinkedList[v];
for (int i = 0; i < v; ++i)
adjList[i] = new LinkedList();
}
// 添加一条边到图
void addEdge(int v, int w) {
adjList[v].add(w);
}
// 广度优先搜索遍历图
void BFS(int s) {
boolean visited[] = new boolean[V];
LinkedList<Integer> queue = new LinkedList<Integer>();
visited[s] = true;
queue.add(s);
while (queue.size() != 0) {
s = queue.poll();
System.out.print(s + " ");
Iterator<Integer> i = adjList[s].listIterator();
while (i.hasNext()) {
int n = i.next();
if (!visited[n]) {
visited[n] = true;
queue.add(n);
}
}
}
}
// 深度优先搜索遍历图
void DFS(int v) {
boolean visited[] = new boolean[V];
DFSUtil(v, visited);
}
// 辅助函数,递归实现深度优先搜索
void DFSUtil(int v, boolean visited[]) {
visited[v] = true;
System.out.print(v + " ");
Iterator<Integer> i = adjList[v].listIterator();
while (i.hasNext()) {
int n = i.next();
if (!visited[n]) {
DFSUtil(n, visited);
}
}
}
}
public class Main {
public static void main(String args[]) {
Graph graph = new Graph(4);
// 添加边到图
graph.addEdge(0, 1);
graph.addEdge(0, 2);
graph.addEdge(1, 2);
graph.addEdge(2, 0);
graph.addEdge(2, 3);
graph.addEdge(3, 3);
System.out.println("广度优先搜索遍历结果:");
graph.BFS(2);
System.out.println("\n深度优先搜索遍历结果:");
graph.DFS(2);
}
```
到了这里,关于揉捻Map-疯狂Java的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!