canvas正交坐标系旋转--监听滚轮-Toy模板网

这篇具有很好参考价值的文章主要介绍了canvas正交坐标系旋转--监听滚轮。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

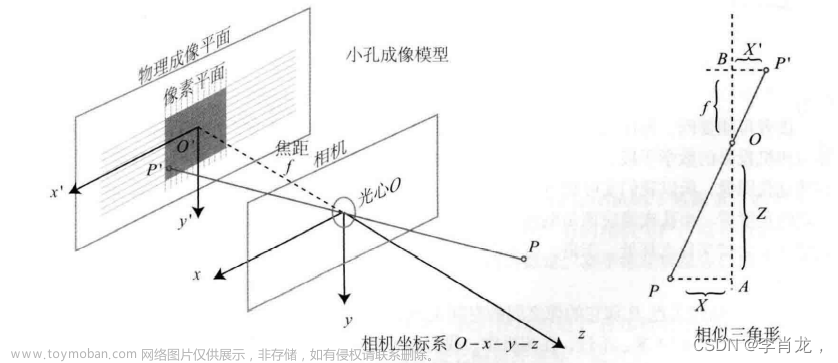
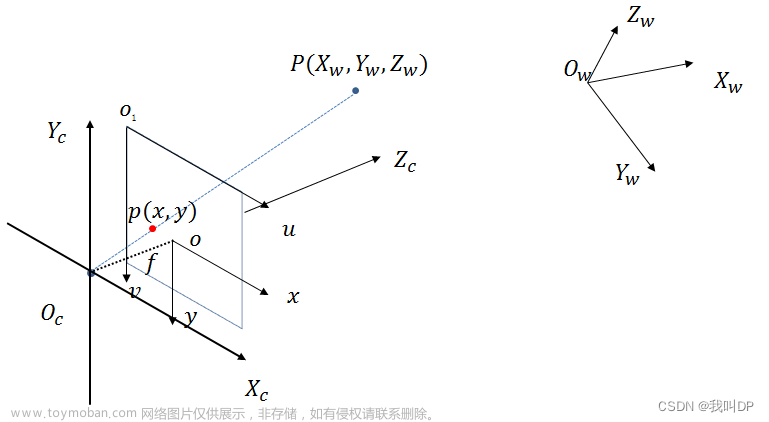
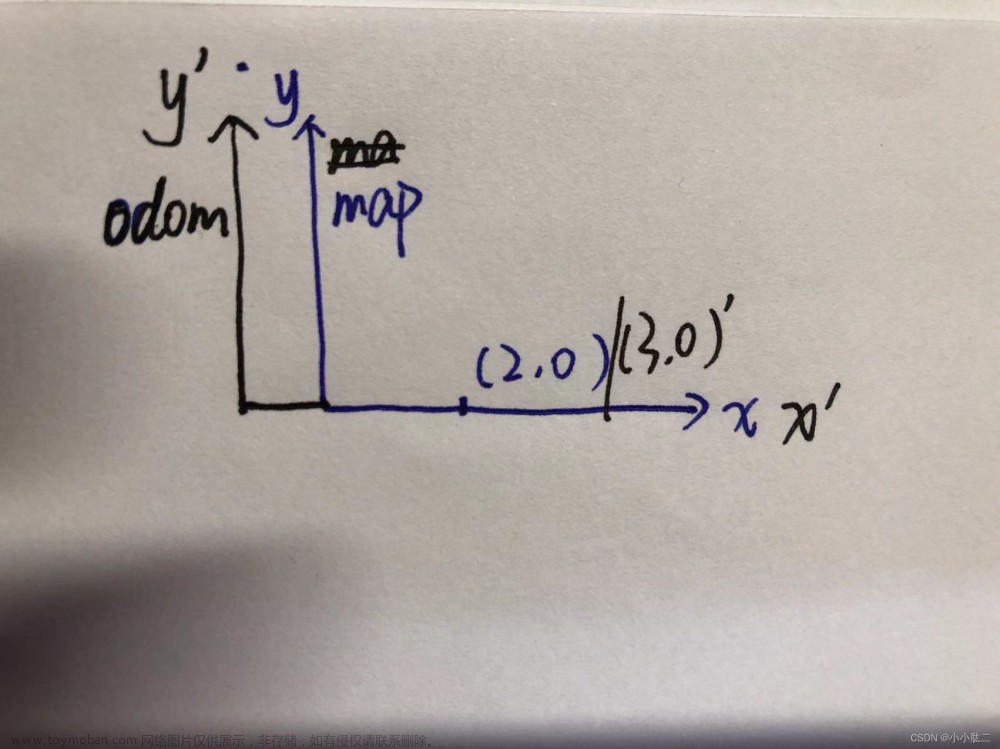
简单学习canvas

<canvas id=“myCanvas” width=200 height=100 ></canvas>
id 是canvas元素的标识；

height,width规定画布大小

直线：

beginPath()方法，指示开始绘图路径： ctx.beginPath();
moveTo()方法将坐标移至直线起点： ctx.moveTo(x,y);
lineTo()方法绘制直线： ctx.lineTo(x,y);
stroke()方法，绘制图形的边界轮廓： ctx.stroke();
closePath()方法，指示闭合绘图路径: ctx.closePath()
    var mycanvas=document.getElementById("canvas");
    var ctx=mycanvas.getContext("2d");
	ctx.beginPath();
	ctx.moveTo(100,100);//移动到绘制点
	ctx.lineTo(200,200);
	ctx.strokeStyle="#000000"; //指定描边颜色
	ctx.stroke();
三角形：
	var mycanvas=document.getElementById("canvas");
    var ctx=mycanvas.getContext("2d");
	ctx.beginPath();
	ctx.moveTo(100,200);
	ctx.lineTo(400,200);
	ctx.lineTo(250,400);
	ctx.closePath();//闭合绘图
	ctx.strokeStyle="#000000";
	ctx.stroke();

矩形：

绘制矩形：rect(x,y,width,height)；

绘制矩形边框：strokeRect(x, y, width, height);

绘制填充矩形：fillRect(x, y, width, height);

擦除指定矩形区域：clearRect(x, y, width, height);
	var mycanvas=document.getElementById("canvas");
	var ctx=mycanvas.getContext("2d");
 
	//rect()函数调用
	ctx.beginPath();
	ctx.rect(20,20,100,50);
	ctx.stroke();

圆形：arc(centerx,centery,radius,startAngle,endAngle,antiClockwise);

centerx,centery 圆弧中心点坐标

Radius 半径

startAngle 起始弧度

endAngle 终止弧度

antiClockwise 是否按逆时针方向绘图，是一个可选参数，默认为false（即顺时针方向绘图）
弧度 = 角度* ( Math.PI / 180 )
	var mycanvas=document.getElementById("canvas");
	var ctx=mycanvas.getContext("2d");
	//arc()函数调用
	ctx.beginPath();
	ctx.arc(100,150,70,0,90*Math.PI/180,true);
	ctx.stroke();

功能实现

<!DOCTYPE html>
<html>

<head>
  <title>Canvas 监听鼠标滚动开启旋转</title>
  <style>
    canvas {
      border: 1px solid #000;
    }
  </style>
</head>

<body>
  <canvas id="myCanvas" width="400" height="200"></canvas>

  <script>
    var canvas = document.getElementById("myCanvas");
    var ctx = canvas.getContext("2d");
    var isRotating = false; // 是否正在进行旋转
    var isEnter = false; // 鼠标按下允许旋转
    var rotationDirection = 0; // 旋转方向：-1表示逆时针，1表示顺时针
    var rotationAngle = 0; // 旋转角度

    // 绘制y轴
    ctx.beginPath();
    ctx.moveTo(100, 100);
    ctx.lineTo(100, 150);
    ctx.stroke();

    // 绘制x轴
    ctx.beginPath();
    ctx.moveTo(100, 150);
    ctx.lineTo(150, 150);
    ctx.stroke();

    // 鼠标按下事件监听器
    canvas.addEventListener("mousedown", function (event) {
      alert('开启旋转功能')
      isEnter = true;
    });

    // 鼠标移动超出画布移除事件监听器
    canvas.addEventListener("mousemove", function (event) {
      if (isEnter) {
        let content = canvas.getBoundingClientRect()
        let x = event.clientX
        let y = event.clientY
        if (x >= content.right - 10 || x <= content.left + 10 || y >= content.bottom - 10 || y <= content.top + 10) {
          isEnter = false
          alert('关闭旋转功能')
        };
      }
    });

    // 鼠标滚动事件监听器
    canvas.addEventListener("wheel", function (event) {
      event.preventDefault(); // 阻止滚动页面
      if (isEnter) {
        isRotating = true;
        rotationDirection = event.deltaY > 0 ? -1 : 1; // deltaY > 0 表示向下滚动，逆时针旋转；deltaY < 0 表示向上滚动，顺时针旋转
      }
    });

    // 鼠标滚动停止事件监听器
    var timeoutId;
    canvas.addEventListener("wheel", function () {
      clearTimeout(timeoutId);
      timeoutId = setTimeout(function () {
        isRotating = false;
      }, 100); // 停止滚动后100毫秒内不再进行旋转
    });

    // 动画循环函数
    function animate() {
      if (isRotating) {
        rotationAngle += rotationDirection * 1; // 每次增加/减少旋转角度
        rotateLine(rotationAngle);
      }

      requestAnimationFrame(animate);
    }

    function rotateLine(angle) {
      ctx.clearRect(0, 0, canvas.width, canvas.height);

      // 绘制原始直线
      // ctx.beginPath();
      // ctx.moveTo(50, 100); // 起点
      // ctx.lineTo(350, 100); // 终点
      // ctx.stroke();

      // 保存当前画布状态
      ctx.save();

      // 平移画布到直线中心点
      var centerX = 100;
      var centerY = 150;
      ctx.translate(centerX, centerY);

      // 旋转画布
      ctx.rotate((angle * Math.PI) / 180);

      // 绘制y轴
      ctx.beginPath();
      ctx.moveTo(0, 0);
      ctx.lineTo(0, -50);
      ctx.stroke();

      // 绘制x轴
      ctx.beginPath();
      ctx.moveTo(0, 0);
      ctx.lineTo(50, 0);
      ctx.stroke();

      // 恢复画布状态
      ctx.restore();
    }

    animate(); // 启动动画循环
  </script>
</body>

</html>