神经网络小记-优化器-Toy模板网

这篇具有很好参考价值的文章主要介绍了神经网络小记-优化器。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

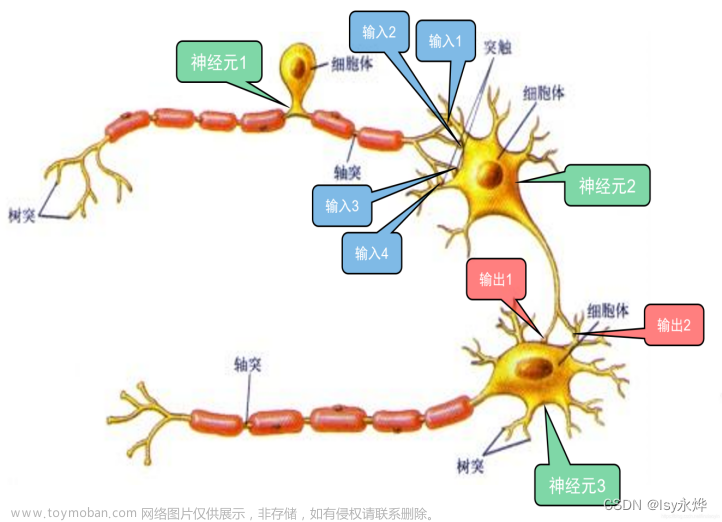
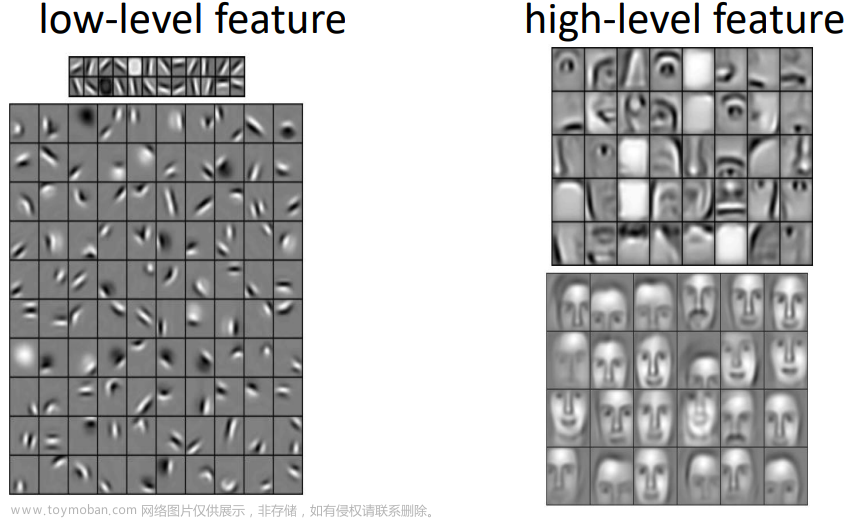
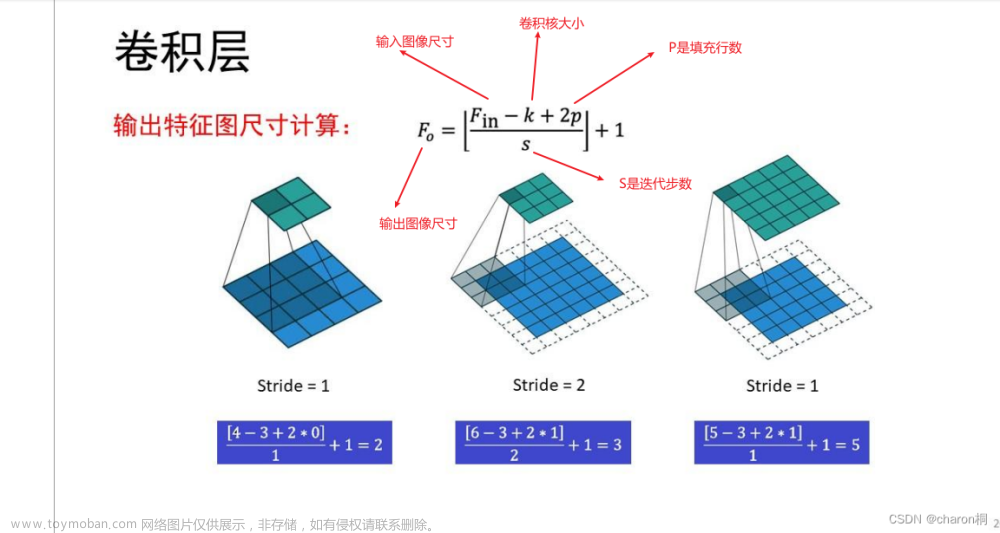
优化器是深度学习中用于优化神经网络模型的一类算法，其主要作用是根据模型的损失函数来调整模型的参数，使得模型能够更好地拟合训练数据，提高模型的性能和泛化能力。优化器在训练过程中通过不断更新模型的参数，使模型逐步接近最优解。

具体来说，优化器的作用包括：

参数更新：优化器根据损失函数计算出的梯度信息来更新模型的参数，使得模型能够朝着损失函数下降的方向调整，从而最小化损失函数。
收敛加速：优化器通过引入动量等技术，可以加速模型的收敛过程，从而更快地找到较好的参数组合。
避免梯度消失或爆炸：在深度神经网络中，由于多层的链式求导可能导致梯度消失或爆炸问题。优化器通过适当的学习率调整和梯度裁剪等技巧，可以缓解这些问题，保证模型的稳定训练。
自适应调整学习率：一些优化器如Adagrad、RMSprop和Adam等具有自适应学习率的特性，能够根据参数梯度的历史信息动态调整学习率，以适应不同参数的学习速度。
防止过拟合：优化器通过在训练过程中更新参数，可以在一定程度上防止模型在训练数据上过度拟合，提高模型的泛化能力。

ps：

同一个优化器通常可以用于分类和回归等不同类型的任务。优化器的作用是通过更新模型的参数来最小化损失函数，而损失函数的选择取决于具体的任务类型。

在深度学习中，优化器的选择一般与损失函数的选择是独立的。优化器的目标是最小化损失函数，而不同类型的损失函数对应着不同的任务。

不论是分类还是回归任务，我们都可以使用相同的优化器来最小化相应的损失函数。优化器的选择不依赖于任务类型，而是根据优化效果、收敛速度等因素来进行选择。可以将同一个优化器用于分类和回归等不同类型的任务，但在使用时需要注意选择合适的损失函数来匹配不同的任务类型。

常见的优化器

随机梯度下降（Stochastic Gradient Descent，SGD）：
- SGD是最基础的优化算法之一，每次迭代从训练数据中随机选择一个样本来计算梯度，并更新模型参数。
- 优点：计算速度较快，易于实现和理解。
- 缺点：可能会陷入局部最优点，梯度更新不稳定。
动量（Momentum）：
- 动量优化器在SGD的基础上加入了动量项，用于加速收敛并减少震荡。
- 动量可以理解为模拟物体在梯度方向上滚动的速度，有助于在陡峭的损失曲面上更快地前进。
- 优点：加速收敛，减少震荡。
- 缺点：可能会在平坦区域陷入局部最优。
自适应学习率优化器：
- Adagrad：Adagrad根据参数的历史梯度信息来调整学习率，适用于稀疏数据。
- RMSprop：RMSprop是对Adagrad的改进版本，通过引入一个衰减系数来防止学习率过快地下降。
- Adam：Adam是结合了动量和RMSprop的优化器，常用于深度学习中，具有较好的性能和鲁棒性。
- 优点：自适应调整学习率，对不同参数使用不同的学习率，收敛速度较快。
- 缺点：需要额外的超参数调优，可能会增加计算开销。
Nesterov Accelerated Gradient（NAG）：
- NAG是对动量优化器的改进版本，在计算梯度时采用模型参数的更新值，有助于提高优化效率。
- 通过提前考虑动量项，可以更准确地估计参数更新，提高参数更新的准确性和稳定性。
AdaDelta：
- AdaDelta是对Adagrad的改进版本，通过动态调整历史梯度信息来避免学习率衰减过快的问题。
- 不需要手动设置全局学习率，参数更新更加稳定。
AdamW（Adam with Weight Decay）：
- AdamW是对Adam的改进版本，在参数更新时对权重衰减进行更准确的处理，可以提高模型的泛化性能。

每种优化器都有其特点和适用场景。在选择优化器时，应考虑数据集的大小、模型的复杂程度、训练时间和计算资源的限制等因素，并通过实验比较不同优化器的性能，选择最适合当前任务的优化算法。

特点与应用场景

下面是各种优化器的特点和应用场景的简要总结，以表格形式呈现：

优化器	特点	应用场景
SGD	最基础的优化器，全局固定学习率，容易陷入局部最优，收敛较慢。	简单问题，数据集较小
Momentum	引入动量项，加速收敛，减少震荡，但可能在平坦区域陷入局部最优。	大规模数据集，复杂模型
Adagrad	自适应学习率，根据参数的历史梯度信息调整学习率，适用于稀疏数据。	稀疏数据集，特征稀疏
RMSprop	对Adagrad的改进，引入衰减系数，防止学习率过快下降。	非平稳数据集，复杂模型
Adadelta	对Adagrad的改进，动态调整学习率，避免全局学习率设置。	大规模数据集，复杂模型
Adam	结合了动量和RMSprop，自适应调整学习率，收敛较快，广泛应用于深度学习。	大多数情况下都适用，复杂模型
AdamW	在Adam的基础上加入权重衰减，提高模型的泛化性能。	大规模数据集，复杂模型
Nadam	在Adam的基础上加入Nesterov Accelerated Gradient，动态调整学习率，收敛更快。	大规模数据集，复杂模型
L-BFGS	二次优化方法，基于拟牛顿法，适用于小数据集和小规模模型。	小数据集，小规模模型

torch中常见优化器

SGD（随机梯度下降）：

import torch.optim as optim

optimizer = optim.SGD(model.parameters(), lr=learning_rate)

Adam（自适应矩估计）：

import torch.optim as optim

optimizer = optim.Adam(model.parameters(), lr=learning_rate)

RMSprop（均方根传递）：

import torch.optim as optim

optimizer = optim.RMSprop(model.parameters(), lr=learning_rate)

Adagrad（自适应学习率方法）：

import torch.optim as optim

optimizer = optim.Adagrad(model.parameters(), lr=learning_rate)

Adadelta：

import torch.optim as optim

optimizer = optim.Adadelta(model.parameters(), lr=learning_rate)

AdamW（带权重衰减的Adam）：

import torch.optim as optim

optimizer = optim.AdamW(model.parameters(), lr=learning_rate)

以上示例中，model.parameters()是用于优化的模型参数，lr是学习率（learning rate），它是优化器的一个重要超参数。可以根据具体任务和数据选择合适的优化器及超参数来进行模型训练和优化。

简单神经网络示例

神经网络一般流程：

前向传播：输入数据通过网络的一系列层，逐层进行线性变换和激活函数处理，得到最终的输出。
损失函数：根据模型的输出和真实标签计算损失，用于衡量模型的预测与真实值之间的差异。
反向传播：通过计算损失函数对模型参数的梯度，将梯度从输出层向输入层传播，用于更新网络参数。
优化器：优化器根据反向传播得到的梯度信息，以一定的优化算法来更新神经网络的参数，从而最小化损失函数。
参数更新：根据优化器计算得到的参数梯度，更新神经网络的权重和偏置，以使模型逐渐收敛于更优的状态。
迭代训练：通过多次迭代前向传播、反向传播和参数更新，使得神经网络在训练集上逐步调整参数，提高模型性能。

重点讲一下优化器：

优化器：优化器是神经网络训练中的重要组成部分，它决定了参数如何根据损失函数的梯度进行更新，从而使得模型逐步优化。
梯度下降：梯度下降是优化器最基本的思想，根据损失函数的梯度方向，对参数进行更新。其中，SGD（随机梯度下降）是最简单的梯度下降方法，但在训练过程中可能会出现震荡和收敛较慢的问题。
优化算法：为了解决梯度下降的问题，出现了多种优化算法。常见的优化器包括：Momentum、Adagrad、RMSprop、Adam等。这些优化算法在梯度下降的基础上引入了动量、学习率调整等机制，以加速收敛和提高优化效果。
超参数调整：优化器有一些重要的超参数，如学习率、动量等。合理选择这些超参数对模型的性能影响很大。通常需要进行超参数调优来找到最优的参数组合。
稳定性与泛化：优化器的选择和超参数的设置对于神经网络的稳定性和泛化性能有很大影响。不同的优化器和超参数组合可能会导致模型陷入局部最优或过拟合。
自适应学习率：近年来，自适应学习率的优化算法变得流行，如Adagrad、RMSprop和Adam。这些算法可以根据参数的历史梯度信息自适应地调整学习率，从而更有效地进行参数更新。
收敛性：优化器的选择也会影响神经网络是否能够达到较好的收敛性，即在合理的迭代次数内，模型能够趋于稳定状态，同时避免过度拟合。因此，在选择优化器时，需要考虑网络结构、数据集规模和训练策略。

在PyTorch中搭建神经网络和选择优化器的重点步骤如下：

定义神经网络模型：首先需要定义神经网络模型的结构。可以使用torch.nn.Module来创建一个自定义的神经网络类，并在其构造函数__init__中定义各层和参数。

import torch
import torch.nn as nn

class MyModel(nn.Module):
    def __init__(self):
        super(MyModel, self).__init__()
        self.fc1 = nn.Linear(in_features, hidden_size)
        self.fc2 = nn.Linear(hidden_size, out_features)
        # 定义其他层...

    def forward(self, x):
        x = self.fc1(x)
        x = torch.relu(x)
        x = self.fc2(x)
        return x

实例化模型和损失函数：在使用模型之前，需要实例化模型，并选择适当的损失函数。同时，需要定义超参数，如学习率（lr）、权重衰减（weight decay）等。

# 实例化模型
model = MyModel()

# 定义损失函数
criterion = nn.CrossEntropyLoss()

# 定义优化器（标注重点）
optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate, weight_decay=weight_decay)

训练循环：在训练过程中，重点是优化器的使用。在每次迭代中，需要先将梯度清零，然后计算模型输出和损失，接着反向传播计算梯度，并最终通过优化器来更新模型参数。

# 训练循环
for epoch in range(num_epochs):
    for inputs, labels in dataloader:
        # 将梯度清零
        optimizer.zero_grad()

        # 前向传播
        outputs = model(inputs)
        loss = criterion(outputs, labels)

        # 反向传播
        loss.backward()

        # 更新模型参数（优化器的重点操作）
        optimizer.step()

验证或测试：在训练后，可以对模型进行验证或测试。在验证或测试阶段，通常不需要进行梯度计算，因此可以使用torch.no_grad()上下文管理器来关闭梯度计算，从而节省内存和计算资源。

# 验证或测试循环
with torch.no_grad():
    for inputs, labels in val_dataloader:
        # 前向传播（无需计算梯度）
        outputs = model(inputs)
        # 其他验证或测试操作...