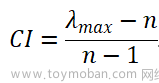一、数据总览
需求:我们需要对各个银行进行评价,A-G为银行的各个指标,下面是银行的数据:

二、代码逐行实现
清空代码和变量的指令
clear;clc;层次分析法
每一行代表一个对象的指标评分
p = [8,7,6,8;7,8,8,7];%每一行代表一个对象的指标评分A为自己构造的输入判别矩阵
%A为自己构造的输入判别矩阵
A=[1,3,1,1/3;
1/3,1,1/2,1/5;
1,2,1,1/3;
3,5,3,1];求特征值特征向量,找到最大特征值对应的特征向量
%%
[n,m]=size(A);
%求特征值特征向量,找到最大特征值对应的特征向量
[V,D]=eig(A); %求特征值和特征向量 D记录特征值 V代表特征向量
%%找到最大的特征值
tzz=max(max(D)); %找到最大的特征值找到最大的特征值位置
c1=find(max(D)==tzz);%找到最大的特征值位置最大特征值对应的特征向量
tzx=V(:,c1);%最大特征值对应的特征向量计算权重
quan1 = tzx/sum(tzx);
%%
%赋权重
quan=zeros(n,1);
for i=1:n
quan(i,1)=tzx(i,1)/sum(tzx);
end一致性检验
Q=quan;
%一致性检验
CI=(tzz-n)/(n-1);
RI=[0,0,0.58,0.9,1.12,1.24,1.32,1.41,1.45,1.49,1.52,1.54,1.56,1.58,1.59];
%判断是否通过一致性检验
CR=CI/RI(1,n);
if CR>=0.1
fprintf('没有通过一致性检验\n');
else
fprintf('通过一致性检验\n');
end显示出所有评分对象的评分值
%显示出所有评分对象的评分值
score=P*Q;
for i=1:length(score)
name=['object_score',num2str(i)];
eval([name,'=score(i)'])
end
Topsis层次分析法
待评价的数据
data=[220 6 30 10 10 5
190 8 25 9 8 3
180 8 28 7 7 4
170 7 23 8 7 2]; 负向指标准化处理
%负向指标准化处理
index=3;
for i=1:length(index)
data1(:,index(i))=(max(data(:,index(i)))-data(:,index(i)))/(max(data(:,index(i)))-min(data(:,index(i))));
end正向指标的标准化处理
%%
%%正向指标准化处理
index_all=1:size(data1,2);
index_all(index)=[]; % 除负向指标外其余所有指标
index=index_all;
%%
for i=1:length(index)
data1(:,index(i))=(data(:,index(i))-min(data(:,index(i))))/(max(data(:,index(i)))-min(data(:,index(i))));
end标准化处理
%%标准化处理
data1=zscore(data);
% for j=1:size(data1,2)
% data1(:,j)= data(:,j)./sqrt(sum(data(:,j).^2));
% end得到加权后的数据
%得到加权重后的数据
w=[0.3724, 0.1003,0.1991, 0.1991,0.0998,0.0485]; %使用求权重的方法求得
R=data1.*w;得到最大值和最小值距离
%得到最大值和最小值距离
r_max=max(R); %每个指标的最大值
r_min=min(R); %每个指标的最小值
d_z = sqrt(sum([(R -repmat(r_max,size(R,1),1)).^2 ],2)) ; %d+向量
d_f = sqrt(sum([(R -repmat(r_min,size(R,1),1)).^2 ],2)); %d-向量
%sum(data,2)对行求和 ,sum(data)默认对列求和得到得分
%得到得分
s=d_f./(d_z+d_f );
Score=100*s/max(s);
for i=1:length(Score)
fprintf('第%d个投标者百分制评分为:%d\n',i,Score(i));
end三、代码整体实现
下面是matlab实现层次分析法和Topsis综合评价法的代码:
%% 层次分析法
clear;clc;
P=[8,7,6,8;7,8,8,7];%每一行代表一个对象的指标评分
%%
%A为自己构造的输入判别矩阵
A=[1,3,1,1/3;
1/3,1,1/2,1/5;
1,2,1,1/3;
3,5,3,1];
%%
[n,m]=size(A);
%求特征值特征向量,找到最大特征值对应的特征向量
[V,D]=eig(A); %求特征值和特征向量 D记录特征值 V代表特征向量
%%
tzz=max(max(D)); %找到最大的特征值
%%
c1=find(max(D)==tzz);%找到最大的特征值位置
%%
tzx=V(:,c1);%最大特征值对应的特征向量
%%
quan1 = tzx/sum(tzx);
%%
%赋权重
quan=zeros(n,1);
for i=1:n
quan(i,1)=tzx(i,1)/sum(tzx);
end
%%
%%%
Q=quan;
%一致性检验
CI=(tzz-n)/(n-1);
RI=[0,0,0.58,0.9,1.12,1.24,1.32,1.41,1.45,1.49,1.52,1.54,1.56,1.58,1.59];
%判断是否通过一致性检验
CR=CI/RI(1,n);
if CR>=0.1
fprintf('没有通过一致性检验\n');
else
fprintf('通过一致性检验\n');
end
%%
%显示出所有评分对象的评分值
score=P*Q;
for i=1:length(score)
name=['object_score',num2str(i)];
eval([name,'=score(i)'])
end
%% TOPSIS
clc;clear;
%%
data=[220 6 30 10 10 5
190 8 25 9 8 3
180 8 28 7 7 4
170 7 23 8 7 2];
%%
index=3;
for i=1:length(index)
data1(:,index(i))=(max(data(:,index(i)))-data(:,index(i)))/(max(data(:,index(i)))-min(data(:,index(i))));
end
%%
%%正向指标准化处理
index_all=1:size(data1,2);
index_all(index)=[]; % 除负向指标外其余所有指标
index=index_all;
for i=1:length(index)
data1(:,index(i))=(data(:,index(i))-min(data(:,index(i))))/(max(data(:,index(i)))-min(data(:,index(i))));
end
data1=zscore(data);
% for j=1:size(data1,2)
% data1(:,j)= data(:,j)./sqrt(sum(data(:,j).^2));
% end
%得到加权重后的数据
w=[0.3724, 0.1003,0.1991, 0.1991,0.0998,0.0485]; %使用求权重的方法求得
R=data1.*w;
%得到最大值和最小值距离
r_max=max(R); %每个指标的最大值
r_min=min(R); %每个指标的最小值
d_z = sqrt(sum([(R -repmat(r_max,size(R,1),1)).^2 ],2)) ; %d+向量
d_f = sqrt(sum([(R -repmat(r_min,size(R,1),1)).^2 ],2)); %d-向量
%sum(data,2)对行求和 ,sum(data)默认对列求和
%得到得分
s=d_f./(d_z+d_f );
Score=100*s/max(s);
for i=1:length(Score)
fprintf('第%d个投标者百分制评分为:%d\n',i,Score(i));
end
对应的原理公式,请跳转到下面的链接:文章来源:https://www.toymoban.com/news/detail-603748.html
http://t.csdn.cn/HXaGB文章来源地址https://www.toymoban.com/news/detail-603748.html
到了这里,关于数学建模学习(4):TOPSIS 综合评价模型及编程实战的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!