vts和faces基础知识
vertices-节点（3是点的三维坐标）
Double类型的矩阵。用来存放所有构成mesh的节点，假设该mesh由N个三维节点构成，那么vertices就是一个N*3的矩阵，vertices(i, j) 表示了第i个节点第j维的坐标。文章来源：https://www.toymoban.com/news/detail-603848.html
faces-面片（3是构成三角形面片的3个点）
Integer类型的矩阵。用来存放节点之间的连接关系。每一个面都由三个节点连接成的三角形构成，假设该mesh由M个三角面片构成，那么faces就是一个M*3的矩阵，faces(i, j)表示了构成第i个面片第j个角的节点序号。
文章来源地址https://www.toymoban.com/news/detail-603848.html
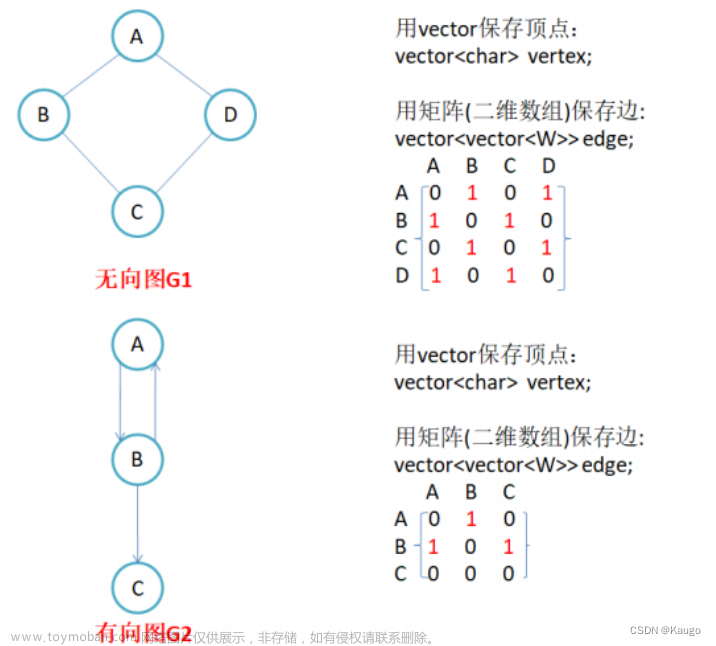
邻接矩阵
- 每个面片都是一个小三角形，因此每个面片都可以延伸出来三条边
- 所以边的数量 = 面片数量 × 3
- 邻接矩阵的size为：边的数量
eg.
(0,1) 1
(0,15) 1
(0,66) 1
...
...
...
邻接距离矩阵（NN=500）
- 实际上是计算离每个点最近的500个距离（NN是聚类中心的个数）
- 邻接距离矩阵的size为：点的数量 × NN
eg.
(0,66) 0.0102
(0,71) 0.0106
(0,67) 0.0200
...
...
...
稀疏矩阵
- 最终，将邻接距离矩阵转化为稀疏矩阵的存储格式即可
- 注意：如果使用lil格式，在调用shortest_path函数可能出现list和int类型不能比较的错误！（解决方法是采用csr格式存储！）
到了这里，关于【三维点云处理】顶点、面片、邻接矩阵、邻接距离矩阵以及稀疏存储概念的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
