深大的夏令营已经结束,筛选入营的保研er就筛选了1/3,280多的入营总人数里面双非只有30左右。
最终虽然凭借机试拿到offer了,但是我感受到了自己的明显短板,比如夏令营的舍友就都有一篇核心论文,甚至还有SCI一区一作的。
既然,学历和没过六级这件事在9月份之前都没办法弥补,现在也只有狂肝科研了,希望9月份预推免之前能够赶出来一点点成果也好。
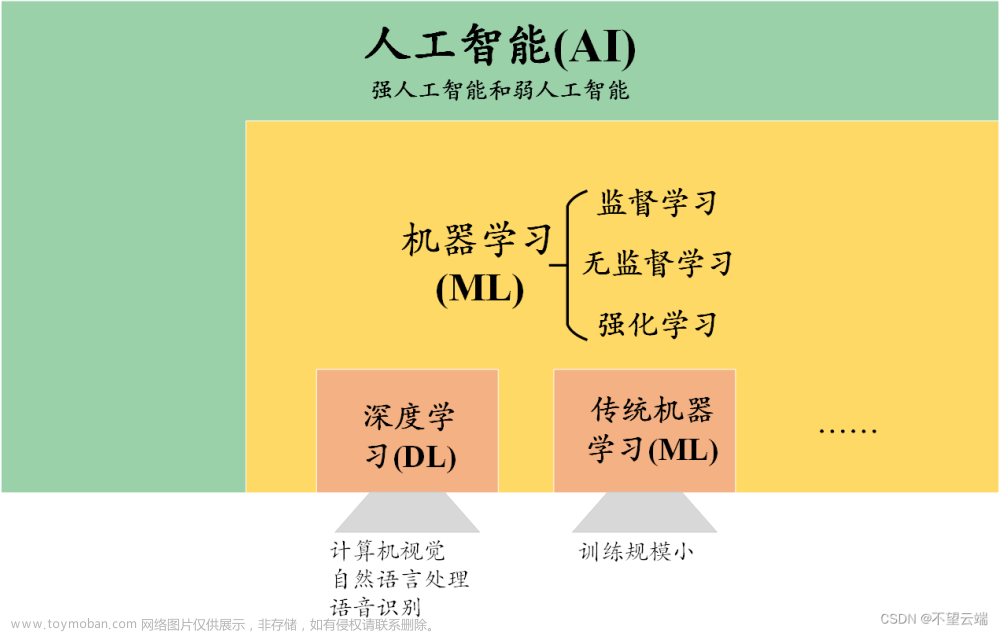
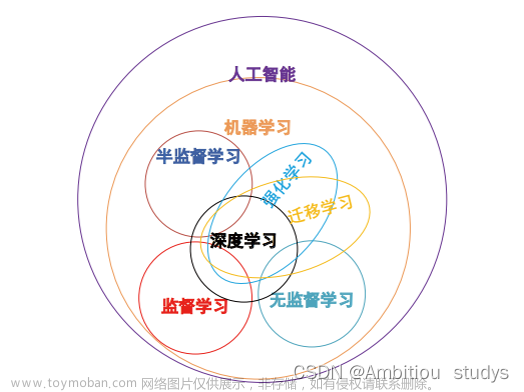
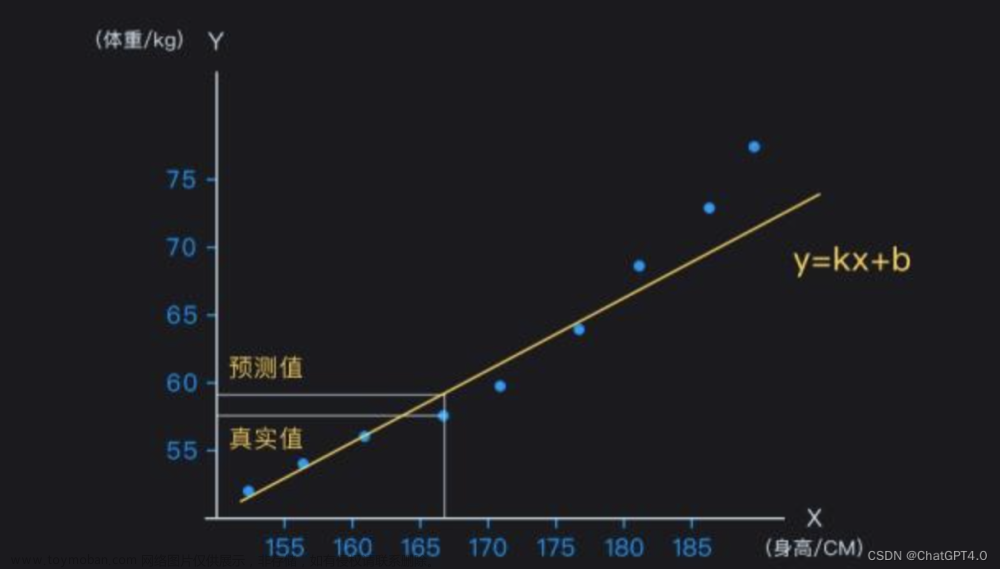
首先把机器学习&&深度学习入门一下,里面包含了一些数学、线性代数、概率论的知识,这刚好也是将来9月预推免的面试中容易被问到的,所以就坚持着全复习完。
1 数据操作
无非就是两件事:
(1)获取数据
(2)处理并存储数据
1.1 入门
张量表示一个由数组组成的数组,可能有多个维度。一维的叫向量,二维的叫矩阵。
下列直接给出代码和注释查看pytorch对张量的操作:
import torch
# 使用arrange创建一个行向量
x = torch.arange(12)
print(x)
# 可以通过张量的shape属性来访问张量(沿每个轴的长度)的形状
print(x.shape)
# 张量中的元素总数
print(x.numel())
# 改变形状而不改变元素的数量和元素值
X = x.reshape(3, 4)
print(X)
# 输出全0、全1矩阵
print(torch.zeros(2, 3, 4))
print(torch.ones(2, 3, 4))
# 创建一个形状为(3,4)的张量,每个元素都是从均值为0,标准差为1的正态分布中随机采样
print(torch.randn(3, 4))
# 还可以直接创建Python列表
print(torch.tensor([[2, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]]))
运行结果:
tensor([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11])
torch.Size([12])
12
tensor([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
tensor([[[0., 0., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.]],
[[0., 0., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.]]])
tensor([[[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.]],
[[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.]]])
tensor([[ 1.5651, -0.2855, -0.4439, 0.5795],
[-1.3375, -1.3290, -0.1183, -1.0676],
[ 0.0334, -2.0030, -1.0172, 0.7654]])
tensor([[2, 1, 4, 3],
[1, 2, 3, 4],
[4, 3, 2, 1]])
1.2 运算符
代码:
import torch
# 对于相同形状的张量,常见的标准算术运算符:加减乘除和指数
x = torch.tensor([1.0, 2, 4, 8])
y = torch.tensor([2, 2, 2, 2])
ans = (x + y, x - y, x * y, x / y, x ** y)
print(ans)
# 也可以实现求幂,如e^x
print(torch.exp(x))
# 张量也可以端对端的连接起来,只需要提供张量列表并给出沿哪个轴连结
# 下面给出的两个张量:
X = torch.arange(12, dtype=torch.float32).reshape((3,4))
Y = torch.tensor([[2.0, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
# 可以发现这是二维的,轴就有两个。轴0表示行,轴1表示列
# 按照轴0来连接,也就是连接行
print(torch.cat((X, Y), dim=0))
# 按照轴1来连接,也就是连接列
print(torch.cat((X, Y), dim=1))
# 通过逻辑运算符构建二元张量:
print(X == Y)
# 若对张量中的所有元素求和,会产生单元素张量
print(X.sum())
运行结果:
(tensor([ 3., 4., 6., 10.]), tensor([-1., 0., 2., 6.]), tensor([ 2., 4., 8., 16.]), tensor([0.5000, 1.0000, 2.0000, 4.0000]), tensor([ 1., 4., 16., 64.]))
tensor([2.7183e+00, 7.3891e+00, 5.4598e+01, 2.9810e+03])
tensor([[ 0., 1., 2., 3.],
[ 4., 5., 6., 7.],
[ 8., 9., 10., 11.],
[ 2., 1., 4., 3.],
[ 1., 2., 3., 4.],
[ 4., 3., 2., 1.]])
tensor([[ 0., 1., 2., 3., 2., 1., 4., 3.],
[ 4., 5., 6., 7., 1., 2., 3., 4.],
[ 8., 9., 10., 11., 4., 3., 2., 1.]])
tensor([[False, True, False, True],
[False, False, False, False],
[False, False, False, False]])
tensor(66.)
1.3 广播机制
如果两个张量的形状不同,可以通过调用广播机制来执行按元素操作:
1、通过适当复制元素来扩展一个或两个数组,以便在转换之后,两个张量具有相同的形状;
2、对生成的数组执行按元素操作。
代码:
import torch
# a为3×1,b为1×2,那么就将a复制列,b复制行
a = torch.arange(3).reshape((3, 1))
b = torch.arange(2).reshape((1, 2))
print(a + b)
运行结果:
tensor([[0, 1],
[1, 2],
[2, 3]])
1.4 索引和切片
第一个元素的索引是0,最后一个元素索引是-1。这个没什么好说的
1.5 节省内存
运行一些操作可能会导致为新结果分配内存。 例如,如果我们用Y = X + Y,我们将取消引用Y指向的张量,而是指向新分配的内存处的张量。
用Python的id()函数演示了这一点, 它给我们提供了内存中引用对象的确切地址。 运行Y = Y + X后,我们会发现id(Y)指向另一个位置。 这是因为Python首先计算Y + X,为结果分配新的内存,然后使Y指向内存中的这个新位置。
before = id(Y)
Y = Y + X
print(id(Y) == before)
最终输出False
但是这并不可取,原因有二:
1、我们不想总是不必要地分配内存。通常情况下,我们希望原地执行这些更新;
2、如果我们不原地更新,其他引用仍然会指向旧的内存位置,这样我们的某些代码可能会无意中引用旧的参数。
执行原地操作代码:
# 使用切片表示法将操作的结果分配给先前分配的数组
Z = torch.zeros_like(Y)
print('id(Z):', id(Z))
Z[:] = X + Y
print('id(Z):', id(Z))
结果:
id(Z): 139931132035296
id(Z): 139931132035296
如果在后续计算中没有重复使用X, 我们也可以使用X[:] = X + Y或X += Y来减少操作的内存开销:
before = id(X)
X += Y
print(id(X) == before)
输出True
2 数据预处理
为了用深度学习解决现实问题,常要从预处理原始数据开始,而不是从准备好的张量格式数据开始。
2.1 读取数据集
代码如下:
import os
import pandas as pd
os.makedirs(os.path.join('D:/Pytorch', 'data'), exist_ok=True)
data_file = os.path.join('D:/Pytorch', 'data', 'house_tiny.csv')
with open(data_file, 'w') as f:
f.write('NumRooms,Alley,Price\n') # 定义列(房间数量、巷子类型、房屋价格)
f.write('NA,Pave,127500\n') # 每行表示一个数据样本
f.write('2,NA,106000\n')
f.write('4,NA,178100\n')
f.write('NA,NA,140000\n')
# 从创建的CSV文件中加载数据集,需要导入pandas包并调入read_csv函数。
data = pd.read_csv(data_file)
print(data)
运行结果:
NumRooms Alley Price
0 NaN Pave 127500
1 2.0 NaN 106000
2 4.0 NaN 178100
3 NaN NaN 140000
2.2 处理缺失值
”NaN“项代表缺失值,可使用插值法解决,用一个替代之弥补缺失值。
通过位置索引iloc,将data分成inputs和outputs,其中前者为data的前两列,后者为最后一列。对于inputs中缺少的数值,用同一列的值替换“NaN”项。
代码:
inputs, outputs = data.iloc[:, 0:2], data.iloc[:, 2]
inputs = inputs.fillna(inputs.mean())
print(inputs)
输出:
NumRooms Alley
0 3.0 Pave
1 2.0 NaN
2 4.0 NaN
3 3.0 NaN
对于inputs中的类别值或离散值,我们将“NaN”视为一个类别。 由于“巷子类型”(“Alley”)列只接受两种类型的类别值“Pave”和“NaN”, pandas可以自动将此列转换为两列“Alley_Pave”和“Alley_nan”。 巷子类型为“Pave”的行会将“Alley_Pave”的值设置为1,“Alley_nan”的值设置为0。 缺少巷子类型的行会将“Alley_Pave”和“Alley_nan”分别设置为0和1。
代码:
inputs = pd.get_dummies(inputs, dummy_na=True)
print(inputs)
结果:
NumRooms Alley_Pave Alley_nan
0 NaN True False
1 2.0 False True
2 4.0 False True
3 NaN False True
3 线性代数
3.1 标量
import torch
x = torch.tensor(3.0)
y = torch.tensor(2.0)
print(x + y, x * y, x / y, x ** y)
最终输出:
tensor(5.) tensor(6.) tensor(1.5000) tensor(9.)
3.2 向量
可以视为标量值组成的列表,具有一定现实意义。如:一个预测贷款风险的模型,可能会将每个申请人与一个向量相关联,其分量与其收入、工作年限、过往违约次数和其他因素相对应。
生成向量:
x = torch.arrange(4)
可以直接通过索引来访问任一元素:
x[3]
3.3 矩阵
import torch
# 输出矩阵A
A = torch.arange(20).reshape(5, 4)
print(A)
# 矩阵转置:若B为A的转置,则对于任意i,j都有B(i,j)=A(j,i)
# 输出A的转置
print(A.T)
# 如果是方阵,那么其转置与其相同
B = torch.tensor([[1, 2, 3], [2, 0, 4], [3, 4, 5]])
print(B == B.T)
结果:
tensor([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11],
[12, 13, 14, 15],
[16, 17, 18, 19]])
tensor([[ 0, 4, 8, 12, 16],
[ 1, 5, 9, 13, 17],
[ 2, 6, 10, 14, 18],
[ 3, 7, 11, 15, 19]])
tensor([[True, True, True],
[True, True, True],
[True, True, True]])
3.4 张量算法的基本性质
任何按元素的一元运算都不会改变其操作数的形状。
1、两个矩阵按元素乘法称为Hadamard积;
2、将张量乘以或加上一个标量不会改变张量的形状,其中张量的每个元素都将与标量相加或相乘。
3.5 降维
import torch
A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
# 直接得到矩阵A的和:
print(A.sum())
# 可以通过指定张量沿哪个轴来降维,如果通过求和所有的行元素来降维,则指定轴0
A_sum_axis0 = A.sum(axis=0)
print(A_sum_axis0, A_sum_axis0.shape)
# 汇总所有列的元素降维
A_sum_axis1 = A.sum(axis=1)
print(A_sum_axis1, A_sum_axis1.shape)
# 沿着行和列对矩阵求和,等价于对所有元素求和
print(A.sum(axis=[0, 1]))
# 求平均值,使用A.mean()或A.sum()/A.numer()
print(A.mean())
# 求平均值也可以沿指定轴降低张量维度
print(A.mean(axis=0))
结果
tensor(190.)
tensor([40., 45., 50., 55.]) torch.Size([4])
tensor([ 6., 22., 38., 54., 70.]) torch.Size([5])
tensor(190.)
tensor(9.5000)
tensor([ 8., 9., 10., 11.])
3.6 点积
对于两个向量x,y,其点积为x的转置乘y,是相同位置的按元素乘积的和。
import torch
x = torch.arange(4, dtype=torch.float32)
y = torch.ones(4, dtype=torch.float32)
print(x, y, torch.dot(x, y))
# 也可以先按元素乘法,然后进行求和来表示两个向量的点积
print(torch.sum(x * y))
结果:
tensor([0., 1., 2., 3.]) tensor([1., 1., 1., 1.]) tensor(6.)
tensor(6.)
3.7 矩阵-向量积
其实就是一种特殊的矩阵乘法,使用函数torch.mv(A,x)即可实现矩阵A和向量x的积
3.8 矩阵-矩阵乘法
使用torch.mm(A,B)即可实现矩阵A和B的相乘。3.7和3.8的矩阵乘法学过线代都知道,不讲解了。
3.9 范数
非正式的说,向量的范数表示一个向量多大。这里的大小不涉及维度,而是分量的大小。
现代中,向量范数是将向量映射到标量的函数f。给定任意向量x,向量范数要满足一些属性:
深度学习中常用L1、L2范数,都是Lp范数的特例。
函数:文章来源:https://www.toymoban.com/news/detail-604945.html
L1范数:torch.abs(u).sum()
L2范数:torch.norm(u)文章来源地址https://www.toymoban.com/news/detail-604945.html
到了这里,关于机器学习&&深度学习——预备知识(上)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!