数据结构栈和队列-Toy模板网

这篇具有很好参考价值的文章主要介绍了数据结构栈和队列。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

3.栈和队列

3.1栈和队列的定义和特点

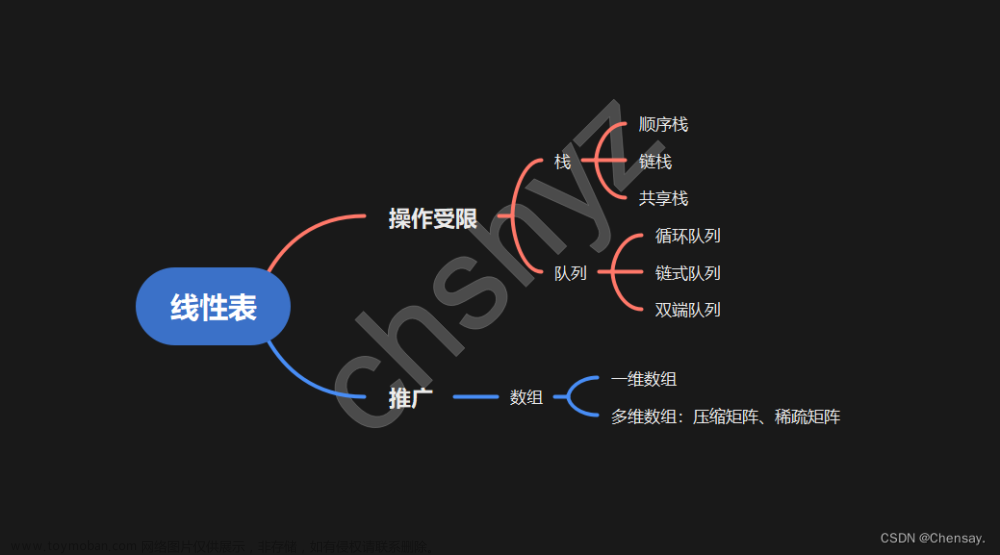
栈和队列是两种常用的、重要的数据结构
栈和队列是限定插入和删除只能在表的 “ 端点 ”进行的线性表
栈和队列是线性表的子集（是插入和删除位置受限的线性表）

栈的应用：

由于栈的操作具有后进先出的固有特性，使得栈成为程序设计中的有用工具。另外，如果问题求解的过程具有“后进先出”的天然特性的话，则求解的算法中也必然需要使用“栈”。如（数制转换、表达式求值、括号匹配的检验、八皇后问题、行编辑程序、函数调用、迷宫求解、递归调用的实现）

队列的应用：

由于队列的操作具有先进先出的特性，使得队列成为程序设计中解决类似排队问题的有用工具。

3.1.1栈的定义和特点

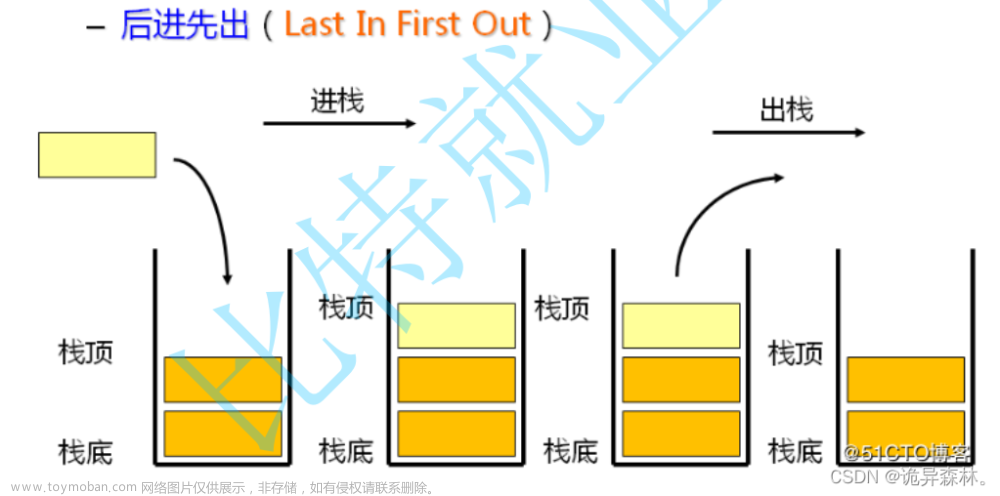
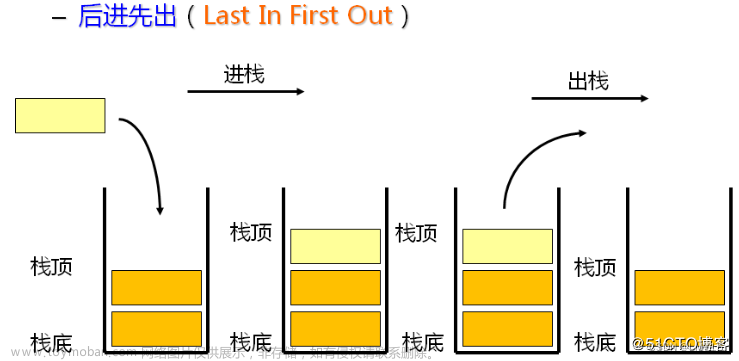
栈是一个特殊的线性表，是限定仅在一端（通常是表尾）进行插入和删除操作的线性表。
又称为后进先出的线性表，简称LIFO结构
存储结构，用顺序栈或链栈存储均可，但以顺序栈更常见。

栈的相关概念

栈是仅在表尾进行插入、删除操作的线性表。

表尾（即an端）称为栈顶Top；表头（即a1端）称为栈底Base

插入元素到栈顶（即表尾）的操作，称为入栈（压栈 PUSH）。

从栈顶（即表尾）删除最后一个元素的操作，称为出栈（POP）。

3.1.2队列的定义和特点

队列是一种先进先出（FIFO）的线性表。在表一端插入（表尾），在另一端（表头）删除。（头删尾插）
存储结构：顺序对或链队，以循环顺序队列更常见。

3.2案例引入

1、进制转换

十进制整数N向其他进制数d（二、八、十六）的转换是计算机实现计算的基本问题。

转换法则：除以d倒取余 n=(n div d)*d + n mod d 其中div为整除运算，mod为求余运算。

例把十进制数159转换为八进制数

（159）₁₀=（237）₈

2、括号匹配的检验

假设表达式中允许包含两种括号：圆括号和方括号

其嵌套的顺序随意，即

（[ ] （））或[（[ ] [ ]）]为正确格式

[（ ] ）] 为错误格式

（[ （））或（（）] ）为错误格式

3.3栈的表示和操作的实现

3.3.1顺序栈的表示和实现

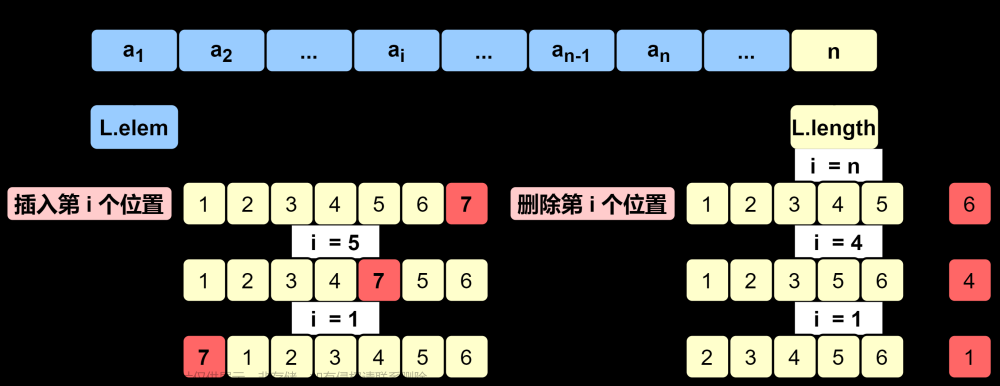
存储方式：同一般线性表的顺序存储结构完全相同，利用一组地址连续的存储单元依次存放自栈底到栈顶的数据元素。栈底一般在低地址端。

附设top指针，指示栈顶元素在顺序栈中的位置。
另设base指针，指示栈底元素在顺序栈中的位置。

但是，为了方便操作，通常top指示真正的栈顶元素之上的下标地址。

另外，用stacksize表示栈可使用的最大容量。

空栈：base == top 是栈空标志

栈满：top - base == stacksize

栈满时的处理方法：

报错，返回操作系统。
分配更大的空间，作为栈的存储空间，将原栈的内容移入新栈。

使用数组作为顺序栈存储方式的特点：简单、方便、但易产生溢出（数组大小固定）

上溢（overflow）：栈已经满，又要压入元素。
下溢（underflow）：栈已经空，还要弹出元素。

顺序栈的表示

#define MAXSIZE 100
typedef struct {
	int* base;  //栈底指针
	int* top;  //栈顶指针
	int stacksize;  //栈可用最大容量
}SqStack;

1、顺序栈的初始化

//顺序栈的初始化
bool InitStack(SqStack& s) {//构造一个空栈
	s.base = new int[MAXSIZE];//或s.base=(int *)malloc(MAXSIZE*sizeof(int))
	if (!s.base) return false;//存储分配失败
	s.top = s.base;//栈顶指针等于栈底指针
	s.stacksize = MAXSIZE;
	return true;
}

2、顺序栈判断栈是否为空

//判断栈是否为空
bool StackEmpty(SqStack s) {
	if (s.top == s.base)return true;
	else return false;
}

3、求顺序栈长度

//求顺序栈长度
int StackLength(SqStack s) {
	return s.top - s.base;
}

4、清空顺序栈

//清空顺序栈
bool ClearStack(SqStack s) {
	if (s.base) s.top = s.base;
	return true;
}

5、销毁顺序栈

bool DestroyStack(SqStack& s) {
	if (s.base) {
		delete s.base;
		s.stacksize = 0;
		s.base = s.top = 0;
	}
	return true;
}

5、顺序栈的入栈

【算法步骤】

判断是否栈满，若满则出错（上溢）
元素e压入栈顶
栈顶指针加1

bool Push(SqStack& s, int e) {
	if (s.top - s.base == s.stacksize) return false;//栈满
	*s.top++ = e;//*s.top=e;  s.top++;
	return true;
}

6、顺序栈的出栈

【算法步骤】

判断是否栈空，若空则出错（下溢）
栈顶指针减1
获取栈顶元素e

bool Pop(SqStack& s, int& e) {
	if (s.top == s.base)//等价以if(StackEmpty(s))
		return false;
	e = *--s.top;// --s.top;  e=*s.top
	return true;
}

3.3.2链栈的表示和实现

链栈的表示：

链栈是运算受限的单链表，只能在链表头部进行操作

typedef struct StackNode {
	int data;
	struct  StackNode* next;
}StackNode,*LinkStack;
LinkStack s;

链表的头指针就是栈顶
不需要头结点
基本不存在栈满的情况
空栈相当于头结点指向空
插入和删除仅在栈顶处执行

1、链栈的初始化

int InitStack(LinkStack& s) {
	LinkStack S;
	S = NULL;
	return true;
}

2、判断链栈是否为空

bool StackEmpty(LinkStack s) {
	if (s == NULL) return true;
	else return false;
}

3、链栈的入栈

bool Push_L(LinkStack& s, int e) {
	LinkStack p = new StackNode;//生成新结点p
	p->data = e;//将新结点数据域置为e
	p->next = s;//进新结点插入栈顶
	s = p;//修改栈顶指针
	return true;
}

4、链栈的出栈

bool Pop_L(LinkStack& s, int& e) {
	if (s == NULL) return false;
	e = s->data;
	LinkStack p;
	p = s;
	s = s->next;
	delete p;
	return true;
}

5、取栈顶元素

int GetTop(LinkStack s) {
	if (s != NULL) return s->data;
}

3.4栈与递归

递归的定义：

若一个对象部分地包含它自己，或用它自己给自己定义，则称这个对象是递归的；
若一个过程直接地或间接地调用自己，则称这个过程是递归的过程。
- 如：递归求n的阶乘
```
long Fact(long n){
  if(n==0) return 1;
  else return n*Fact(n-1);
}
```
- 以下三种情况常常用到递归方法
  - 递归定义的数学函数
    - 阶乘函数
    - 2阶Fibonaci数列
  - 具有递归特性的数据结构
    - 二叉树
    - 广义表
  - 可递归求解的问题
    - 迷宫问题
    - Hanoi塔问题
递归问题——用分治法求解
分治法：对于一个较为复杂的问题，能够分解成几个相对简单的且解法相同或类似的子问题来求解。

必备的三个条件：
1. 能将一个问题转变成一个新问题，而新问题与原问题的解法相同或类同，不同的仅是处理的对象，且这些处理对象是变化有规律的。
2. 可以通过上述转化而使问题简化。
3. 必须有一个明确的递归出口，或称递归的边界。
分治法求解递归问题算法的一般形式：
```
void p(参数表){
  if(递归结束条件) 可直接求解步骤;  -------基本项
  else p(较小的参数);    --------归纳项
}
```
```
long Fact(long n){
  if(n==0) return 1;   //基本项
  else return n*Fact(n-1);  //归纳项
}
```
函数调用过程

调用前，系统完成：
1. 将实参，返回地址等传递给被调用函数
2. 为被调用函数的局部变量分配存储区
3. 将控制转移到被调用函数的入口
调用后，系统完成：
1. 保存被调用函数的计算结果
2. 释放被调用函数的数据区
3. 依照被调用函数保存的返回地址将控制转移到调用函数
当多个函数构成嵌套调用时：遵循后调用的先返回栈
递归的优缺点

优点：结构清晰，程序易读。

缺点：每次调用要生成工作记录，保存状态信息，入栈；返回时要出栈，恢复状态信息。时间开销大。
递归—>非递归

方法1：尾递归、单向递归 -->循环结构

方法2：自用栈模拟系统的运行时栈

3.5队列的表示和操作的实现

相关术语（头删尾插）
- 队列（Queue）是仅在表尾进行插入操作，在表头进行删除操作的线性表。
- 表尾即a_n端,称为队尾；表头即a₁端，称为队头。
- 它是一种**先进先出（FIFO）**的线性表。
- 插入元素称为入队，删除元素称为出队。
- 队列的存储结构为链队或顺序队（常用循环顺序队）。

3.5.1队列的顺序表示和实现

队列的顺序表示——用一维数组base[MAXQSIZE]

#define MAXSIZE 100
typedef struct {
	int* base;//初始化的动态分配存储空间
	int front;//头指针，若队列不空。指向队列头元素
	int rear;//尾指针，若队列不空，指向队列尾元素的下一个位置。
}SqQueue;

初始：front = rear = 0

入队：base [rear] = x ; rear++;

出队：x = base [ front] ; front++;

空队标志：front == rear

设数组大小为MAXSIZE，rear = MAXSIZE时，发出溢出

若front = 0 ，rear=MAXSIZE时，再入队——真溢出
若front ≠ 0 ，rear=MAXSIZE时，再入队——假溢出

数据结构栈和队列,数据结构考研,数据结构,算法

解决假上溢的方法

将队中元素依次向队头方向移动。

缺点：浪费时间。每移动一次，队中元素都要移动。
将队空间设想成一个循环的表，即分配给队列的m个存储单元可以循环使用，当rear为MAXSIZE时，若向量的开始端空着，又可从头使用空着的空间。当front为MAXSIZE时，也是一样。

解决假上溢的方法——引入循环队列

base[0]接在base[MAXSIZE-1]之后，若rear+1==M，则令rear=0；

实现方法：利用模（mod，C语言中：%）运算。

插入元素：Q.base[Q.rear] = x;

Q.rear = (Q.rear + 1) % MAXSIZE;

删除元素：x = Q.base[s.front]

Q.front = (Q.front + 1) % MAXSIZE;

数据结构栈和队列,数据结构考研,数据结构,算法

如何判断队空和队满？

解决方案：

另外设一个标志以区别队空、队满。
另设一个变量，记录元素个数。
少用一个元素空间

循环队列解决队满时判断方法——少用一个元素空间：

数据结构栈和队列,数据结构考研,数据结构,算法

队空：front == rear

队满：（rear + 1）% MAXSIZE == front

1、队列的初始化

bool InitQueue(SqQueue& Q) {
	Q.base = new int[MAXSIZE];//分配数组空间
	//或Q.base=(int*)malloc(MAXSIZE*sizeof(int));
	if (!Q.base) return false;//存储分配失败
	Q.front = Q.rear = 0;//头指针尾指针置为0，队列为空
	return true;
}

2、求队列的长度

int QueueLength(SqQueue Q) {
	return ((Q.rear - Q.front+MAXSIZE)%MAXSIZE);
}

3、循环队列入队

bool EeQueue(SqQueue& Q, int e) {
	if ((Q.rear + 1) % MAXSIZE == Q.front) return false;//队满
	Q.base[Q.rear] = e;//新元素加入队尾
	Q.rear = (Q.rear + 1) % MAXSIZE;//队尾指针+1
	return true;
}

4、循环队列出队

bool DeQueue(SqQueue& Q, int& e) {
	if (Q.front == Q.rear) return false;//队空
	e = Q.base[Q.front];//保存队头元素
	Q.front = (Q.front + 1) % MAXSIZE;//队头指针+1
	return true;
}

5、取队头元素

int GetHead(SqQueue Q) {
	if (Q.front != Q.rear)//队列不为空
		return Q.base[Q.front];//返回队头指针元素的值，队头指针不变
}

3.5.2队列的链式表示和实现

若用户无法估计所用队列的长度，则宜采用链队列

数据结构栈和队列,数据结构考研,数据结构,算法

链队列的类型定义：

typedef struct Qnode {
	int data;
	struct Qnode* next;
}QNode,*QuenePtr;

typedef struct {
	QuenePtr front;//队头指针
	QuenePtr rear;//队尾指针
}LinkQueue;

链队列运算指针变化状况：

数据结构栈和队列,数据结构考研,数据结构,算法

1、链队列初始化

bool InitQueue_L(LinkQueue& Q) {
	Q.front = Q.rear = (QuenePtr)malloc(sizeof(QNode));
	if (!Q.front) return false;
	Q.front->next = NULL;
	return true;
}

2、销毁链队列（补充）

算法思想：从队头结点开始，依次释放所有结点。文章来源地址https://www.toymoban.com/news/detail-604969.html

bool DestroyQueue(LinkQueue& Q) {
	QNode* p;
	while (Q.front) {
		p = Q.front->next;
		free(Q.front);
		Q.front = p;
    //或者Q.rear=Q.front->next; free(Q.front); Q.front=Q.rear;
	}
	return true;
}

3、将元素e入队

bool EnQueue_L(LinkQueue& Q, int e) {
	QNode* p;
	p = (QuenePtr)malloc(sizeof(QNode));
	if (!p) return false;
	p->data = e;
	p->next = NULL;
	Q.rear->next = p;
	Q.rear = p;
	return true;
}

4、链队列出队

bool DeQueue_L(LinkQueue& Q, int& e) {
	if (Q.front == Q.rear) return false;
	QNode* p;
	p = Q.front->next;
	e = p->data;
	Q.front->next = p->next;
	if (Q.rear == p)Q.rear = Q.front;
	delete p;
	return true;
}

5、求链队列的队头元素

bool GetHead(LinkQueue Q, int& e) {
	if (Q.front == Q.rear) return false;
	e = Q.front->next->data;
	return true;
}

到了这里，关于数据结构栈和队列的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！

数据结构栈和队列

3.栈和队列

3.1栈和队列的定义和特点

3.1.1栈的定义和特点

3.1.2队列的定义和特点

3.2案例引入

1、进制转换

2、括号匹配的检验

3.3栈的表示和操作的实现

3.3.1顺序栈的表示和实现

1、顺序栈的初始化

2、顺序栈判断栈是否为空

3、求顺序栈长度

4、清空顺序栈

5、销毁顺序栈

5、顺序栈的入栈

6、顺序栈的出栈

3.3.2链栈的表示和实现

1、链栈的初始化

2、判断链栈是否为空

3、链栈的入栈

4、链栈的出栈

5、取栈顶元素

3.4栈与递归

3.5队列的表示和操作的实现

3.5.1队列的顺序表示和实现

1、队列的初始化

2、求队列的长度

3、循环队列入队

4、循环队列出队

5、取队头元素

3.5.2队列的链式表示和实现

1、链队列初始化

2、销毁链队列（补充）

3、将元素e入队

4、链队列出队

5、求链队列的队头元素

相关文章

觉得文章有用就打赏一下文章作者

支付宝扫一扫打赏

微信扫一扫打赏

支付宝扫一扫领取红包，优惠每天领

二维码1

二维码2