两个数组的dp问题(2)--动态规划-Toy模板网

这篇具有很好参考价值的文章主要介绍了两个数组的dp问题(2)--动态规划。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

一)交错字符串:

97. 交错字符串 - 力扣（LeetCode）

一)确定一个状态标识:

如果我选择s1的一段区间，再进行选择s2得一段区间，那么s3这个字符串的长度就已经固定

预处理:在s1字符串s2字符串和s3字符串前面加上一个虚拟字符，让下标从1开始进行计数

如果要是从1号位置开始进行计数的话会变得十分方便

s1=" "+s1

s2=" "+s2

s3=" "+s3

状态表示:dp[i][j]就表示s1中的[1，i]区间内的字符串以及s2[1，j]区间内的字符串能否拼接成s3的[1，i+j]区间内的字符串，如果能够拼接而成，那么里面存的值就是true，否则里面的值就是false；

二)根据状态表示推导状态转移方程:根据最后一个位置的情况来分情况进行讨论

1)如果s1的[0，i]区间和s2的[0，j]区间能够拼接成s3字符串的[0，i+j]区间，那么s3字符串的的i+j位置要么是等于s1的i字符，要么是等于s2的j字符，要么都不等于

2)如果能够拼接而成，要么等于s1的最后一个字符，要么等于s2的最后一个字符

if(s1[i]==s3[i+j])那么此时应该研究的就是s1字符串的[0，i-1]区间内的字符串和s2字符串的[0，j]区间内的字符串是否能够构成s3字符串从[0，i-1+j]的子串

if(s1[i]==s3[i+j]) dp[i][j]=dp[i-1][j]

if(s2[j]==s3[i+j]) dp[i][j]=dp[i][j-1]

三)初始化:

引入空串，在原始的dp表中新增加了一行并且新增加了一列

1)dp[0][0]表示的是第一个字符串是空串况且第二个字符串也是空串，空串拼接空串当然可以

2)现在来看dp[0][i]位置的值(i>0)，如果第一个字符串为空，第二个字符串不为空，如果想拼接成第三个字符串，那么必须是对应位置的字符相等才可以，也就是第二个字符串和第三个字符串必须完全相等才可以，如果出现一个位置对应字符不相等，全部白玩

四)填表顺序+返回值:从上向下填写每一行，每一行从左向右进行编写，返回值是dp[m][n]
class Solution {
    public boolean isInterleave(String s1, String s2, String s3) {
        if(s1.length()+s2.length()!=s3.length()) return false;
//1.先针对初始字符串进行预处理
        s1="-"+s1;
        s2="-"+s2;
        s3="-"+s3;
        char[] array1=s1.toCharArray();
        char[] array2=s2.toCharArray();
        char[] array3=s3.toCharArray();
//2.创建一个dp表,先进行初始化
    boolean[][] dp=new boolean[array1.length][array2.length];
    dp[0][0]=true;
    for(int i=1;i<array2.length;i++){
          if(array2[i]==array3[i]) dp[0][i]=true;
          else break;
    }
    for(int j=1;j<array1.length;j++){
        if(array1[j]==array3[j]) dp[j][0]=true;
        else break;
    }
//3.填表
    for(int i=1;i<array1.length;i++){
        for(int j=1;j<array2.length;j++){
dp[i][j]=(array1[i]==array3[i+j]&&dp[i-1][j])||(array2[j]==array3[i+j]&&dp[i][j-1]);
        }
    }
//4.返回值
     return dp[array1.length-1][array2.length-1];
    }
}
思考一下这么写为什么不对

二)两个字符串删除的最小ASCILL码和

712. 两个字符串的最小ASCII删除和 - 力扣（LeetCode）

我们可以将这个题转化成求两个字符串的公共子序列的ASCILL码和最大的那一个

分析:我们求的是两个字符串的所有公共子序列中，ASCILL码值的最大和，运用正难则反的思想

一)定义一个状态表示:

dp[i][j]表示从s1字符串[0，i]区间和s2字符串[0，j]区间的所有给公共子序列中，两个字符串的公共子序列中ASCILL码和最大和

二)根据状态标识推导状态转移方程:根据最后一个位置来划分问题，分情况讨论

要找公共子序列，是从s1里面拉出一个子序列，也需要从s2里面拉出一个子序列，判断他们是否是公共子序列，如果是，求出它们的和，从而找到最大和

if(s1[i]==s2[j]) dp[i][j]=dp[i-1][j-1]+s1[i]的ASCILL码值

if(s1[i]!=s2[j]) dp[i][j]=Math.max(dp[i-1][j] dp[i][j-1],dp[i-1][j-1])

既然要求公共子序列，那么一定是包含一下几种情况:

1)包含s1[i]，包含s2[j]:if(s1[i]==s2[j])->dp[i][j]=dp[i-1][j-1]+s1[i]的ASCILL码

2)包含s1[i]，不包含s2[j]:dp[i][j]=dp[i][j-1](但是这个状态标识和状态2是完全不对等的，这个状态包含了包含s1[i]，不包含s2[j]和不包含s1[i]，不包含s2[j]，但是一定是不包含dp[i][j-1]

3)不包含s1[i]，包含s2[j]:dp[i][j]=dp[i-1][j]和上面同理，不包含i一定可以保证，但是也是可以不包含s2[j]的，也是可能会包括s2[j]的

4)不包含s1[i]不包含s2[j] dp[i][j]=dp[i-1][j-1]

上面的2 3情况已经包含了第四种情况

三)初始化+填表顺序+返回值:

1)引入空串:引入一行一列，第一行表示第一个字符串是空的情况，第一列表示第一个字符串是空的情况，当有一个字符串是空的时候，根本就无法找到ASCILL码值最大的子序列的和，其实连最长公共子序列都找不到，所以他们的最长公共子序列的ASCIL码值的和就是0

2)下标的映射关系:多加一行多加一列之后，下标已经统一向右下角移动了一位，此时下标一定要-1

3)填表顺序:从上到下，每一行从左向右

4)返回值:两个字符串的ASCILL总和-2*dp[m][n]
class Solution {
    public int minimumDeleteSum(String s1, String s2) {
    int sum=0;
    for(int i=0;i<s1.length();i++){
        sum+=s1.charAt(i);
    }
    for(int i=0;i<s2.length();i++){
        sum+=s2.charAt(i);
    }
    s1="_"+s1;
    s2="_"+s2;
    char[] array1=s1.toCharArray();
    char[] array2=s2.toCharArray();
    int[][] dp=new int[array1.length][array2.length];
    for(int i=1;i<array1.length;i++){
        for(int j=1;j<array2.length;j++){
            if(array1[i]==array2[j]){
                dp[i][j]=dp[i-1][j-1]+array1[i];
            }else{
                dp[i][j]=Math.max(dp[i-1][j],dp[i][j-1]);
//从包含i位置不包含j位置,不包含i位置包含j位置
            }
        }
    }
  return sum-dp[array1.length-1][array2.length-1]*2;
    }
}

三)最长重复子数组:

718. 最长重复子数组 - 力扣（LeetCode）

一)定义一个状态表示:

1)我们选择第一个数组[0，i]这段区间，我们选择第二个数组[0，j]这段区间，我们想要的是最长重复子数组，我们在第一个区间内找到所有的子数组，我们在第二个区间内找到所有的子数组，我们统计一下两个区间内最长的重复子数组统计一下长度即可

dp[i][j]表示第一个数组在[0，i]区间的所有子数组和[0，j]区间内第二个数组的所有子数组中最长的那一个，如果选择[0，i]区间内的所有子数组来研究问题，但是这个状态表示的范围太大了，当进行推导下一个位置的时候，会用到前面的状态

2)选取[0，i]区间内的所有子数组作为研究对象，当我们去进行推导i+1状态的时候，会是使用到前面这些状态的，当我们在进行推导i+1状态的值的时候，想要跟在某一个子数组的后面，就必须跟在i位置的后面，所以我们在进行推导i+1状态的时候，还需要看一下i位置子数组的状态，但是最长重复子数组可能都不包括i，可能是i-1，但是进行研究子序列问题的时候，i+1都是可以跟在前面的所有值的后面的，但是子数组就不行了

3)研究子数组问题:

dp[i][j]表示nums1以i位置为结尾的所有的子数组

以及nums2以j位置为结尾的所有子数组中

dp[i][j]存的值是最长重复子数组的长度

二)根据状态表示推到状态转移方程:

if(nums[i]==nums2[j]) dp[i][j]=dp[i-1][j-1]+1

else dp[i][j]=0
class Solution {
    public int findLength(int[] nums1, int[] nums2) {
        int max=0;
        int[][] dp=new int[nums1.length+1][nums2.length+1];
        for(int i=1;i<=nums1.length;i++){
            for(int j=1;j<=nums2.length;j++){
                if(nums1[i-1]==nums2[j-1]){
                    dp[i][j]=dp[i-1][j-1]+1;
                }else{
                    dp[i][j]=0;
                }
                 max=Math.max(dp[i][j],max);
            }
        }
    return max;
    }
}

五)最长公共前缀:

14. 最长公共前缀 - 力扣（LeetCode）

一)定义一个状态表示:dp[i]表示以i位置为结尾的字符串数组的最长公共前缀

二)根据状态表示状态转移方程:

1)根据最近的一步来进行划分问题，如果发现这个字符串所有的i位置的元素都是相等的，那么最长公共前缀就是dp[i-1]+"ch"，但是如果出现了abcde和hhhhe这种情况，如果发现以i-1位置为结尾的最长公共公共前缀是空，那么dp[i]也是空，虽然相等但是没有最长公共前缀

2)如果发现各个字符串在i位置的元素不是全部都相等，那么直接返回dp[i-1]的值
class Solution {
    public String longestCommonPrefix(String[] strs) {
        //dp[i]表示以i位置为结尾字符串数组的最长公共前缀
        String minString=strs[0];
        for(String str:strs){
            if(minString.length()>=str.length()) 
              minString=str;
        }
        if(minString.equals("")) return "";
//1.先进行初始化
       String[] dp=new String[minString.length()];
       char ch=strs[0].charAt(0);
       dp[0]=ch+"";
       for(String str:strs){
           if(str.charAt(0)!=ch){
               dp[0]="";
               break;
           }
       }
//2.进行填表
     for(int i=1;i<minString.length();i++){
           ch=minString.charAt(i);
          for(int j=0;j<strs.length;j++){
              if(strs[j].charAt(i)!=ch){
                return dp[i-1];
              }
          }
        if(!dp[i-1].equals("")) dp[i]=dp[i-1]+ch;
        else dp[i]="";
      }
    return dp[minString.length()-1];
    }
}

class Solution {
    public String longestCommonPrefix(String[] strs) {
//1.先找到最小字符串
        String minString=strs[0];
        for(String str:strs){
            if(str.length()<minString.length()){
                minString=str;
            }
        }
    int m=minString.length();
//2.创建dp表
   String[] dp=new String[minString.length()+1];
   dp[0]="";
  for(int i=0;i<strs.length;i++){
      strs[i]="-"+strs[i];
  }
  minString="-"+minString;
   System.out.println(Arrays.toString(strs));
 for(int i=1;i<=m;i++){
     char ch=minString.charAt(i);
     for(String str:strs){
         if(str.charAt(i)!=ch){
             return dp[i-1];
         }
     }
     dp[i]=dp[i-1]+ch;
   }
 return dp[m];
    }
}

六)最长有效括号:

32. 最长有效括号 - 力扣（LeetCode）

解法1:动态规划

1)定义一个状态标识:dp[i]表示以i位置为结尾，最长有效括号的长度

众所周知，既然以i位置为结尾，最长有效括号的长度，那么必须是以右括号为结尾才可以是有效括号，如果单单以左括号为结尾，那么也算不上是有效括号

2)根据状态表示推到状态转移方程

2.1)if(array[i]==')'&&array[i-1]=='(') dp[i]=dp[i-2]+2;

2.2)if(array[i]=="(") dp[i]=0;

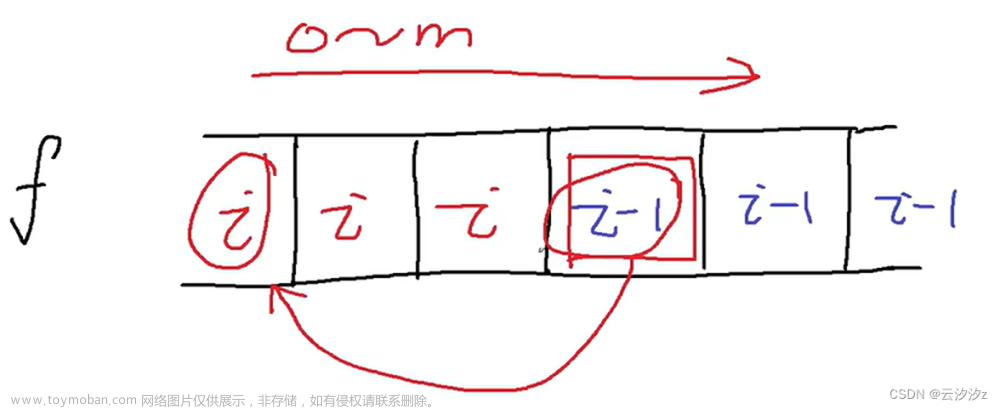
2.3)if(array[i]==")"&&array[i-1]==")") dp[i]=2+dp[i-1]+dp[i-dp[i-1]-2]
class Solution {
    public int longestValidParentheses(String s) {
        char[] array=s.toCharArray();
        int[] dp=new int[array.length];
        int max=0;
//i-1不会越界,因为当i=0的时候,无论是左括号还是有括号,最长有效括号长度永远是0
//这道题的初始化有点恶心,我们需要考虑i-2越界的情况,i-dp[i-1]-1越界的情况
//dp[i-dp[i-1]]-2越界的情况
//况且还要找array[i-dp[i-1]-1]==')'的情况
        for(int i=1;i<array.length;i++){
            if(array[i]=='(') dp[i]=0;
            else if(array[i]==')'&&array[i-1]=='('){
                dp[i]=(i-2>=0?dp[i-2]:0)+2;
            }else if(array[i]==')'&&array[i-1]==')'){
                if(i-dp[i-1]-1<0||array[i-dp[i-1]-1]==')'){
                    dp[i]=0;
                }else{
                    dp[i]=(i-dp[i-1]>=2?dp[i-dp[i-1]-2]:0)+dp[i-1]+2;
                }
            }
            max=Math.max(max,dp[i]);
        }
    System.out.println(Arrays.toString(dp));
    return max;
    }
}

解法2:栈

1)我们使用一个栈，栈里面存放的是上一个没有进行成功匹配的位置，首先在栈里面存放一个-1，因为是说如果括号是完全匹配的，那么根本就不存在不匹配成功的位置，此时栈里面根本没有元素，所以要使用最后一个字符的位置减去-1

2)求一个字符串中某一段区间的长度:当前最后一个字符下标的索引-要计算长度的第一个字符的下标的前一个位置

具体做法是我们始终保持栈底元素为当前已经遍历过的元素中，最后一个没有被匹配的右括号的下标，这样的做法主要是考虑了边界条件的处理，栈里其他元素维护左括号的下标：

1)对于遇到的每个左括号，我们将它的下标放入栈中
2)对于遇到的每个右括号，我们先弹出栈顶元素表示匹配了当前右括号

3)如果弹出元素以后发现，如果栈为空，说明当前的右括号为没有被匹配的右括号，我们将其下标放入栈中来更新我们之前提到的，最后一个没有被匹配的右括号的下标
4)如果栈不为空，当前右括号的下标减去栈顶元素即为，以该右括号为结尾的最长有效括号的长度文章来源地址https://www.toymoban.com/news/detail-605488.html
class Solution {
    public int longestValidParentheses(String s) {
        char[] array=s.toCharArray();
        Stack<Integer> stack=new Stack<>();
        stack.push(-1);
        int max=0;
        for(int i=0;i<array.length;i++){
            if(array[i]=='('){
                stack.push(i);
            }else{
                stack.pop();
                if(stack.isEmpty()){
                    stack.push(i);//如果栈里面没有元素说明当前没有左括号和当前右括号匹配,就把当前位置的右括号放到栈里面说明是第一个不匹配的位置
                }else{
//如果栈不为空,那么直接求出有效括号的长度
                     max=Math.max(max,i-stack.peek());
                }
            }
        }
    return max;
    }
}

到了这里，关于两个数组的dp问题(2)--动态规划的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！