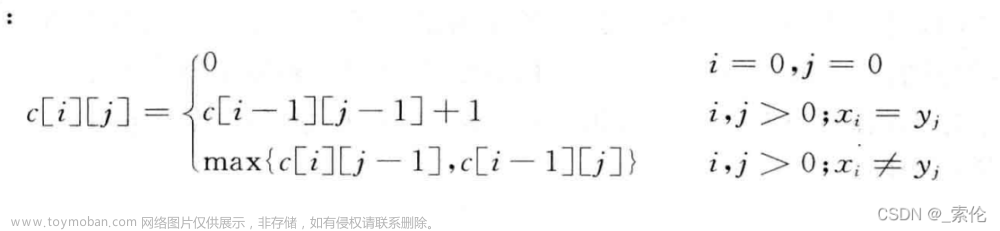说明
最长连续子序列问题算是动态规划问题中的一个小分支,这里单独写一篇文章介绍。至于动态规划基础问题和详细的处理步骤我在我的另一篇文章中详细介绍过。具体解决步骤请移步观看——动态规划基础篇。如果想了解01背包问题和滚动数组相关内容请移步观看——动态规划——01背包问题。
例题讲解
1.最长连续递增序列
给定一个未经排序的整数数组,找到最长且连续递增的子序列,并返回该序列的长度。
连续递增的子序列 可以由两个下标 l 和 r(l < r)确定,如果对于每个 l <= i < r,都有 nums[i] < nums[i + 1] ,那么子序列 [nums[l], nums[l + 1], …, nums[r - 1], nums[r]] 就是连续递增子序列。
提示:
- 1 <= nums.length <= 104
- 109 <= nums[i] <= 109
1.1确定dp(dp table)数组及其下标的含义
dp[i]:以nums[i]结尾的最长的递增且连续的子序列长度为dp[i]。
注意这里的以nums[i]的子序列必须是连续递增序列,例如nums=[1,5,7,4],dp[3]=1,即以nums[3]=4为结尾的连续递增子序列为[4]。
1.2确定递推公式
我们如何得到dp[i],注意dp数组的含义:以nums[i]结尾的最长的递增且连续的子序列长度为dp[i]。因为要求是连续的递增子数列,所以dp[i]只能由dp[i-1]递推得出,如果nums[i]>nums[i-1]显然,dp[i]=dp[i-1]+1,如果nums[i]<=nums[i-1],nums[i]无法接在nums[i-1]后面此种情况直接跳过。
综上分析,递推公式如下:
if(nums[i]>nums[i-1]){
dp[i]=dp[i-1]+1;
}
1.3dp数组初始化
因为以下标i为结尾的数组的连续递增的⼦序列⻓度最少也应该是1,即就是nums[i]这⼀个元素,所以dp[i]初始值应该为1。
1.4代码示例
class Solution {
public int findLengthOfLCIS(int[] nums) {
int len=nums.length;
int[] dp=new int[len];
Arrays.fill(dp,1);
int max=1;
for(int i=1;i<len;i++){
if(nums[i]>nums[i-1]){
dp[i]=dp[i-1]+1;
}
max=Math.max(max,dp[i]);
}
return max;
}
}
注意:这里我来讲一下这段代码" max=Math.max(max,dp[i])"的意义,首先我们将dp数组初始值都设为以,如果nums[i]>nums[i-1],则dp[i]=dp[i-1]+1,但是如果nums[i]<=nums[i-1],我们没有对dp数组做任何处理,这样我们虽然是从i=1开始递推,但是我们不能保证dp[len-1]是最大值,也就是我们需要的结果,因为如果nums[len-1]<=nums[len-2]那么dp[len-1]不会做任何处理,等于初始值1,所以我们不能保证dp数组最后一个值是递推的最终结果,所以我们需要额外借用一个变量max保存最大值。
2.最长递增子序列
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
提示:
- 1 <= nums.length <= 2500
- 104 <= nums[i] <= 104
2.1确定dp(dp table)数组及其下标的含义
dp[i]:以nums[i]结尾的最长的递增子序列长度为dp[i]。
注意这里的以nums[i]的子序列必须是递增序列,例如nums=[1,5,7,4],dp[3]=2,即以nums[3]=4为结尾的递增子序列为[1,4]。
2.2确定递推公式
这道题和第一道例题最大的区别就是,不再要求递增数列是连续的。所以我们要的道dp[i],就需要让nums[i]和前j个元素(j<i)比较,如果nums[i]>nums[j],那么dp[i]=Math.max(dp[i],dp[j]+1)。至于为什么dp[i]=Math.max(dp[i],dp[j]+1),而不是dp[i]=dp[j]+1,这道题讲解最后我会给大家举一个例子帮助大家理解。
综上分析,递推公式如下:
if(nums[i]>nums[j]){
dp[i]=Math.max(dp[i],dp[j]+1);
}
2.3dp数组初始化
因为以下标i为结尾的数组的递增的⼦序列⻓度最少也应该是1,即就是nums[i]这⼀个元素,所以dp[i]初始值应该为1。
2.4代码示例
class Solution {
public int lengthOfLIS(int[] nums) {
int len=nums.length;
int[] dp=new int[len];
Arrays.fill(dp,1);
int max=1;
for(int i=1;i<len;i++){
for(int j=0;j<i;j++){
if(nums[i]>nums[j]) dp[i]=Math.max(dp[i],dp[j]+1);
}
max=Math.max(max,dp[i]);
}
return max;
}
}
虽然现在这道题代码已经写出来了,但是大家可能还会疑问为什么dp[i]=Math.max(dp[i],dp[j]+1),而不是dp[i]=dp[j]+1,因为前面这里我并没有详细展开叙述,而是一笔带过,这里我会该大家举一个具体的例子,帮助大家理解。
假设nums=[1,5,7,4,3,8]
当我们从i=1,j=0开始遍历,显然nums[1]>nums[0],所以dp[1]=Math.max(dp[1],dp[0]+1)=2;
当我们从i=2,j=0开始遍历,显然nums[2]>nuns[0],nums[2]>nums[1],所以最终dp[2]=3;
当我们从i=3,j=0开始遍历,显然nums[3]=4,他只大与nums[0]=1,所以最终dp[3]=2;
当我们从i=4,j=0开始遍历,显然nums[4]=3,他只大与nums[0]=1,所以最终dp[4]=2;
当我们从i=5,j=0开始遍历,此时nums[5]=8,是这个数组中最大数字,当遍历道j=2时,nums[5]=8>nums[2]=7,所以dp[5]=Math.max(dp[5],dp[2]+1)=4,注意这里直接让dp[5]=dp[2]+1也等于4,因为dp[5]初始值为1,但是当遍历到j=3时,nums[5]=8>nums[3]=4,如果直接让dp[5]=dp[3]+1,按照之前的推理,dp[3]=2,那么dp[5]=dp[3]+1=3,显然这是不对的。
所以我们要保存最大的结果就到让dp[5]=Math.max(dp[5],dp[3]+1);
通过这个例子,其实我们也可以发现假如nums=[1,5,7,4],那么dp[3]=2,同样dp数组的最后一个值并不是地推过程中产生的最大值,所以我们同样需要一个额外的变量max保留递推过程中产生的最大值。
3.最长重复子数组
给两个整数数组 nums1 和 nums2 ,返回 两个数组中 公共的 、长度最长的子数组的长度 。
提示:
- 1 <= nums1.length, nums2.length <= 1000
- 0 <= nums1[i], nums2[i] <= 100
3.1确定dp(dp table)数组及其下标的含义
dp[i][j]:代表以 nums1[i-1] 结尾和 nums2[j-1] 结尾构成的最长公共子数组的长度。
例如nums1=[0,1,1,1,1],nums2=[1,0,1,0,1];
公共子数组为nums1中的[0,1]和nums2中的[0,1],但是要注意nums2中的[0,1]由两个一个时以第2个1结尾的[0,1]数组另一个是以第3个1结尾的[0,1]数组。
我们只需要找到最大的公共子数组即可。
3.2确定递推公式
dp[i][j]=dp[i-1][j-1]+1;
3.3dp数组初始化
根据dp[i][j]的定义,dp[i][0] 和dp[0][j]其实都是没有意义的!
但dp[i][0] 和dp[0][j]要初始值,因为 为了⽅便递归公式dp[i][j] = dp[i - 1][j - 1] + 1;
所以dp[i][0] 和dp[0][j]初始化为0。
举个例⼦A[0]如果和B[0]相同的话,dp[1][1] = dp[0][0] + 1,只有dp[0][0]初始为0,正好符合递推公式
逐步累加起来。
3.4代码示例
class Solution {
public int findLength(int[] nums1, int[] nums2) {
int len1=nums1.length,len2=nums2.length;
int[][] dp=new int[len1+1][len2+1];
int res=0;
for(int i=1;i<=len1;i++){
for(int j=1;j<=len2;j++){
if(nums1[i-1]==nums2[j-1]){
dp[i][j]=dp[i-1][j-1]+1;
}
res=Math.max(res,dp[i][j]);
}
}
return res;
}
}
4.最长公共子序列
给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回 0 。
一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
例如,“ace” 是 “abcde” 的子序列,但 “aec” 不是 “abcde” 的子序列。
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。
提示:
- 1 <= text1.length, text2.length <= 1000
- text1 和 text2 仅由小写英文字符组成。
4.1确定dp(dp table)数组及其下标的含义
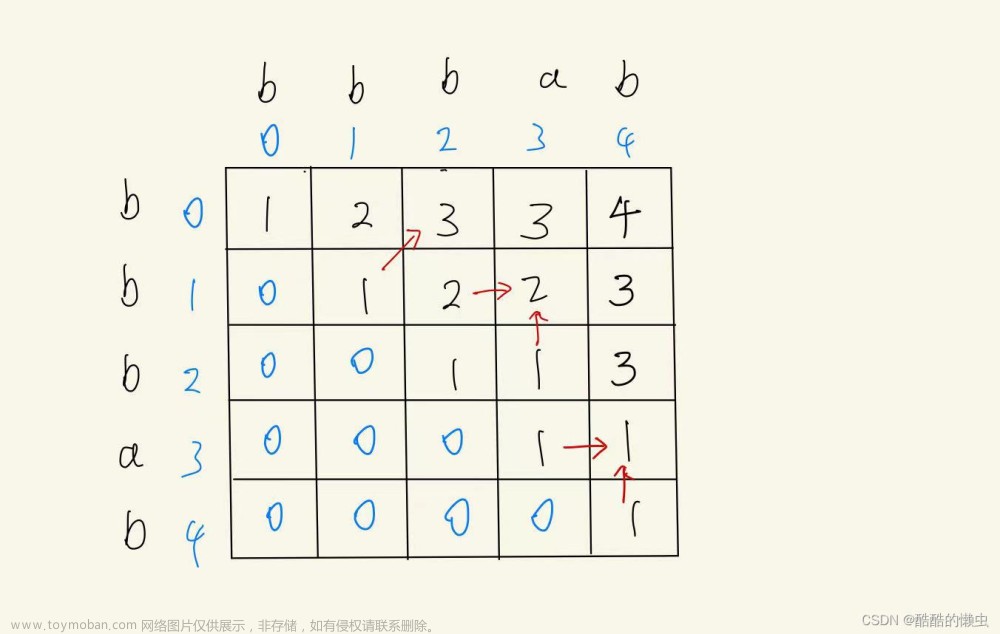
dp[i][j]:表示第一个字符串前i-1个字符和第二个字符串前j-1个字符组成的最长公共字符串的长度。
4.2确定递推公式
如果text1.charAt(i-1)==text.charAt(j-1),显然dp[i][j]=dp[i-1][j-1],如text1=“abde”,text2=“acd”,text1.charAt(2)==text2.charAt(2),显然dp[3][3]=dp[2][2]+1,即"abd"和"acd"组成的最长公共字符串的长度等于"ab"和"ac"组成的公共子串的长度+1;
如果text1.charAt(i-1)==text.charAt(j-1),注意dp数组的含义:表示第一个字符串前i-1个字符和第二个字符串前j-1个字符组成的最长公共字符串的长度。还是上面的例子,dp[2][1]=1,即"ab"和"a"组成的最长公共字符串的长度为1,dp[1][2]=1,即即"a"和"ac"组成的最长公共字符串的长度为1,假设此时i=2,j=2,text1.charAt(i-1)=text1.charAt(1),text2.charAt(j-1)=text1.charAt(1),此时text1.charAt(1)!=text2.charAt(1)即’b’!=‘c’,注意dp[2][2]表示第一个字符串前1个字符和第二个字符串前1个字符组成的最长公共字符串的长度(字符串字符下标从0开始),此时dp[2][2]有两种选择要么dp[2][2]=dp[2][1],要么dp[2][2]=dp[1][2],二者去最大值即可,即dp[2][2]=Math.max(dp[2][1],dp[1][2]);
综上,递推公式为:文章来源:https://www.toymoban.com/news/detail-605593.html
if(text1.charAt(i-1)==text2.charAt(j-1)){
dp[i][j]=dp[i-1][j-1]+1;
}else{
dp[i][j]=Math.max(dp[i][j-1],dp[i-1][j]);
}
4.3dp数组初始化
根据dp[i][j]的定义,dp[i][0] 和dp[0][j]其实都是没有意义的!
但dp[i][0] 和dp[0][j]要初始值,因为 为了⽅便递归公式dp[i][j] = dp[i - 1][j - 1] + 1;
所以dp[i][0] 和dp[0][j]初始化为0。
举个例⼦text1.charAt(0)如果和text2.charAt(0)相同的话,dp[1][1] = dp[0][0] + 1,只有dp[0][0]初始为0,正好符合递推公式
逐步累加起来。文章来源地址https://www.toymoban.com/news/detail-605593.html
4.4代码示例
class Solution {
public int longestCommonSubsequence(String text1, String text2) {
int len1=text1.length(),len2=text2.length();
int[][] dp=new int[len1+1][len2+1];
for(int i=1;i<=len1;i++){
for(int j=1;j<=len2;j++){
if(text1.charAt(i-1)==text2.charAt(j-1)){
dp[i][j]=dp[i-1][j-1]+1;
}else{
dp[i][j]=Math.max(dp[i][j-1],dp[i-1][j]);
}
}
}
return dp[len1][len2];
}
}
到了这里,关于动态规划---最长连续子序列问题的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!