25.4 matlab里面的10中优化方法介绍——最速下降法（matlab程序）-Toy模板网

这篇具有很好参考价值的文章主要介绍了25.4 matlab里面的10中优化方法介绍——最速下降法（matlab程序）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

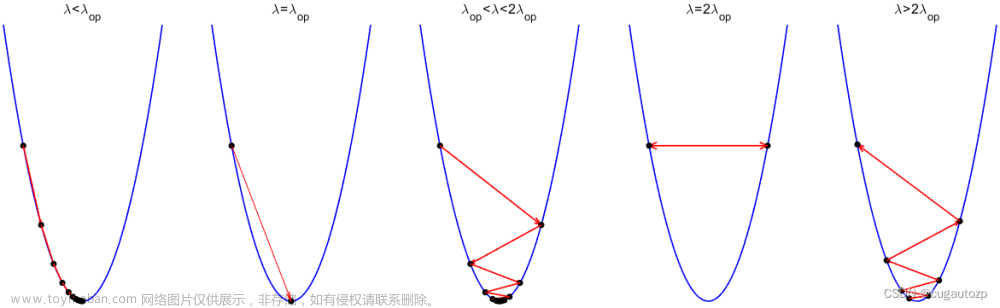
1.简述

matlab实现最速下降法
定义：沿负梯度方向进行搜索的算法（负梯度方向为最速下降方向）
算法步骤：

步0：选取初始点x0，容许误差是e=[0~1],令k=1

步1：计算目标函数的梯度gk=▽f(xk))

若 ||gk||<=e，即达到误差要求,立即停止计算，并输出xk作为近似最优解。

步2:取搜索方向为dk=-gk（即负梯度方向）。

步3：利用线搜索技术确定步长σ

文章来源地址https://www.toymoban.com/news/detail-606534.html

（这里采用Armijo准则来求步长）

步长为α

k=β是给定的，所以要求出mk

Amrijo准则就是

（1）给定βε（0~1），αε（0，0.5），令m=0

（2）若不等式

f(xk+β^m*dk)<=f(xk)*β^m*gk'*dk

成立，则令mk=m，Xk+1=xk+β^m*dk.停止运算，输出mk得到步长

（3）若不满足上述不等式，则令m=m+1，然后回到第二步。

步4：确定步长后，令Xk+1=Xk+σk*dk，k=k+1，转步骤1.

matlab 具体代码如下：

2.代码

主程序：

%% 用最速下降法求最优化解
f1204 = inline('x(1)*(x(1)-5-x(2))+x(2)*(x(2)-4)','x');%目标函数
grad=inline('[2*x(1)-5-x(2),-x(1)+2*x(2)-4]','x'); %目标函数的梯度函数
x0 = [1 4];
TolX = 1e-4;
TolFun = 1e-9;
MaxIter = 100;
dist0=1;
[xo,fo] = Opt_Steepest(f1204,grad,x0,TolX,TolFun,dist0,MaxIter)

子程序：

function [xo,fo] = Opt_Steepest(f,grad,x0,TolX,TolFun,dist0,MaxIter)
% 用最速下降法求最优化解
%输入：f为函数名 grad为梯度函数
%x0为解的初值 TolX,TolFun分别为变量和函数的误差阈值
%dist0为初始步长 MaxIter为最大迭代次数
%输出: xo为取最小值的点 fo为最小的函数值
% f0 = f(x(0))

%%%%%%判断输入的变量数，设定一些变量为默认值
if nargin < 7
MaxIter = 100; %最大迭代次数默认为100
end
if nargin < 6
dist0 = 10; %初始步长默认为10
end
if nargin < 5
TolFun = 1e-8; %函数值误差为1e-8
end
if nargin < 4
TolX = 1e-6; %自变量距离误差
end
%%%%%第一步，求解的初值的函数值
x = x0;
fx0 = feval(f,x0);
fx = fx0;
dist = dist0;
kmax1 = 25; %线性搜索法确定步长的最大搜索次数
warning = 0;
%%%%%迭代计算求最优解

for k = 1: MaxIter
g = feval(grad,x);
g = g/norm(g); %求在x处的梯度方向
%%线性搜索方法确定步长
dist = dist*2; %令步长为原步长的二倍
fx1 = feval(f,x-dist*2*g);
for k1 = 1:kmax1
fx2 = fx1;
fx1 = feval(f,x-dist*g);
if fx0 > fx1+TolFun & fx1 < fx2 - TolFun %fx0 > fx1 < fx2，
den = 4*fx1 - 2*fx0 - 2*fx2;num = den - fx0 + fx2; %二次逼近法
dist = dist*num/den;
x = x - dist*g; fx = feval(f,x); %确定下一点
break;
else
dist = dist/2;
end
end
if k1 >= kmax1
warning = warning + 1; %无法确定最优步长
else
warning = 0;
end
if warning >= 2|(norm(x - x0) < TolX&abs(fx - fx0) < TolFun)
break;
end
x0 = x;
fx0 = fx;
end
xo = x; fo = fx;
if k == MaxIter
fprintf('Just best in %d iterations',MaxIter);
end