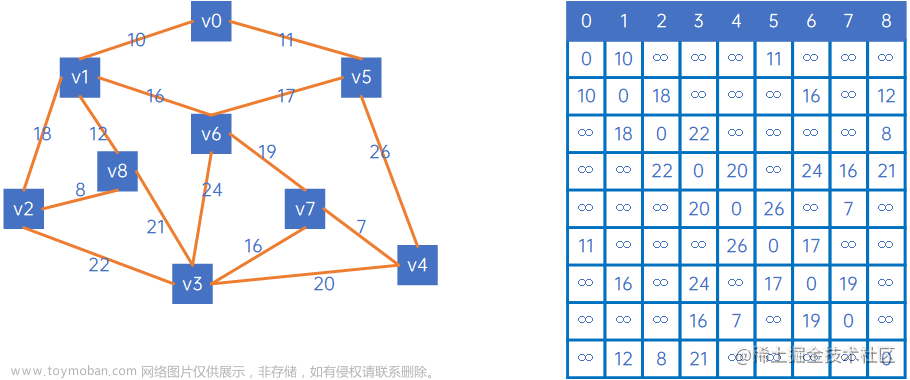
Prim算法:
(只看点,不看边,适合边较多的图,即稠密图)
Kruskal算法:
是一种按权值的递增次序选择合适的边来构造最小生成树的方法;(稀疏图)
Dijkstra算法:
适合带权有向图和带权无向图求单源最短路径;
不适合含负取值的图,求最短路径;
1 . 单选题 简单 7分
对于有n个顶点的带权连通图,它的最小生成树是指图中任意一个______。
A.由n-1条权值最小的边构成的子图
B.由n-l条权值之和最小的边构成的子图
C.由n个顶点构成的极大连通子图
D.由n个顶点构成的极小连通子图,且边的权值之和最小
回答正确
解析文章来源地址https://www.toymoban.com/news/detail-606787.html
每棵生成树中所有边上的权值之和可能不同,其中边上的权值之和最小的生成树称为图的最小生成树;
2 . 单选题 简单 7分
用Prim算法求一个连通的带权图的最小生成树,在算法执行的某时刻,已选取的顶点集合U={1,2,3},已选取的边的集合TE={(1,2),(2,3)},要选取下一条权值最小的边,应当从______ 组边中选取。
A.{(1,4),(3,4),(3,5),(2,5)}
B.{(4,5),(1,3),(3,5)}
C.{(1,2),(2,3),(3,5)}
D.{(3,4),(3,5),(4,5),(1,4)}
回答正确
解析
U={1,2,3},V-U={4,5,……} 候选边只能是这两个顶点集之间的边;
3 . 单选题 简单 7分
用Prim算法求一个连通的带权图的最小生成树,在算法执行的某时刻,已选取的顶点集合U={1,2,3},边的集合TE={(1,2),(2,3)},要选取下一条权值最小的边,不可能从______ 组中选取。
A.{(1,4),(3,4),(3,5),(2,5)}
B.{(1,5),(2,4),(3,5)}
C.{(1,2),(2,3),(3,1)}
D.{(1,4),(3,5),(2,5),(3,4)}
回答正确
解析
4 . 单选题 简单 7分
用Kruskal算法求一个连通的带权图的最小生成树,在算法执行的某时刻,已选取的边集合TE={(1,2),(2,3),(3,5)},要选取下一条权值最小的边,不可能选取的边是______。
A.(1,3)
B.(2,4)
C.(3,6)
D.(1,4)
回答正确
解析
5 . 单选题 简单 7分
对某个带权连通图构造最小生成树,以下说法中正确的是______。
Ⅰ.该图的所有最小生成树的总代价一定是唯一的
Ⅱ.其所有权值最小的边一定会出现在所有的最小生成树中
Ⅲ.用普里姆(Prim)算法从不同顶点开始构造的所有最小生成树一定相同
Ⅳ.使用普里姆算法和克鲁斯卡尔(Kruskal)算法得到的最小生成树总不相同
A.仅Ⅰ
B.仅Ⅱ
C.仅Ⅰ、Ⅲ
D.仅Ⅱ、Ⅳ
回答正确
解析
若有较小的相等权值,最小生成树可能不唯一,但是其代价是唯一的;
第二个的错误是,所有权值最小的边一定会……它也有可能形成环;
第三个,最小生成树一定相同,,,,,
第四个:若是无相同权值,生成树一定相同;但若有较小相等权值,生成树可能会不同;
6 . 单选题 简单 7分
n个顶点e条边的带权有向图采用邻接矩阵存储,求最短路径的Dijkstra算法的时间复杂度为______。
A.O(n)
B.O(n+e)
C.O(n2)
D.O(ne)
回答正确
解析
7 . 单选题 简单 7分
Dijkstra算法是______ 方法求出图中从某顶点到其余顶点的最短路径的。
A.按长度递减的顺序
B.按长度递增的顺序
C.通过深度优先遍历
D.通过广度优先遍历
回答错误
解析
8 . 单选题 简单 7分
用Dijkstra算法求一个带权有向图G中从顶点0出发的最短路径,在算法执行的某时刻,S={0,2,3,4},下一步选取的目标顶点可能是______。
A.顶点2
B.顶点3
C.顶点4
D.顶点7
回答正确
解析
9 . 单选题 简单 7分
用Dijkstra算法求一个带权有向图G中从顶点0出发的最短路径,在算法执行的某时刻,S={0,2,3,4},则以后可能修改最短路径是______。
A.从顶点0到顶点2的最短路径
B.从顶点0到顶点3的最短路径
C.从顶点0到顶点4的最短路径
D.从顶点0到顶点1的最短路径
回答正确
解析
0,2,3,4已经在集合S中,不需要再次去判断到其路径长度;
所以再次判断是判断不在集合S中的定点;
10 . 单选题 简单 7分
有一个顶点编号为0~4的带权有向图G,现用Floyd算法求任意两个顶点之间的最短路径,在算法执行的某时刻,已考虑了0~2的顶点,现考虑顶点3,则以下叙述中正确的是______。
A.只可能修改从顶点0~2到顶点3的最短路径
B.只可能修改从顶点3到顶点0~2的最短路径
C.只可能修改从顶点0~2到顶点4的最短路径
D.所有其他两个顶点之间的路径都可能被修改
回答正确
解析
11 . 单选题 简单 6分
在有向图G的拓扑序列中,若顶点i在顶点j之前,则以下情况不可能出现的是______。
A.G中有边<i,j>
B.G中有一条从顶点i到顶点j的路径
C.G中没有边<i,j>
D.G中有一条从顶点j到顶点i的路径
回答正确
解析
12 . 单选题 简单 6分
若用邻接矩阵存储有向图,矩阵中主对角线以下的元素均为零,则关于该图拓扑序列的结论是______。
A.存在,且唯一
B.存在、且不唯一
C.存在,可能不唯一
D.无法确定是否存在
回答正确
解析
邻接矩阵存储有向图且主对角线以下的元素均为0,说明在此有向图中,1 为起点,n 为终点;
任何一个顶点都不能到达比其他号码小的顶点。在这种有向图中拓扑序列是存在的,但可能唯一,也可能不唯一;
如:只有两个顶点的有向图,拓扑序列就唯一,但是,三个顶点的有向图中拓扑序列就可能不唯一;
13 . 单选题 简单 6分
若一个有向图中的顶点不能排成一个拓扑序列,则可断定该有向图______。
A.是个有根有向图
B.是个强连通图
C.含有多个入度为0的顶点
D.含有顶点数目大于1的强连通分量
回答正确
解析
14 . 单选题 简单 6分
以下关于图拓扑排序的叙述中正确的是______。 Ⅰ.任何无环的有向图,其顶点都可以排在一个拓扑序列中。 Ⅱ.若n个顶点的有向图有唯一的拓扑序列,则其边数必为n-1。 Ⅲ.在一个有向图的拓扑序列中,若顶点a在顶点b之前,则图中必有一条边<a,b>
A.仅Ⅰ
B.仅Ⅰ、Ⅲ
C.仅Ⅱ、Ⅲ
D.Ⅰ、Ⅱ和Ⅲ
回答错误
解析
15 . 多选题 简单 6分
在用Prim和Kruskal算法构造最小生成树时,前者更适合于 ① ,后者更适合于 ② 。
A.有向图
B.无向图
C.稀疏图
D.稠密图文章来源:https://www.toymoban.com/news/detail-606787.html
回答正确
解析
到了这里,关于数据结构作业—第十三周---- Prim算法 Kruskal算法 Dijkstra算法的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!