Leetcode-每日一题【剑指 Offer II 010. 和为 k 的子数组】-Toy模板网

这篇具有很好参考价值的文章主要介绍了Leetcode-每日一题【剑指 Offer II 010. 和为 k 的子数组】。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

题目

给定一个整数数组和一个整数 k ，请找到该数组中和为 k 的连续子数组的个数。

示例 1：

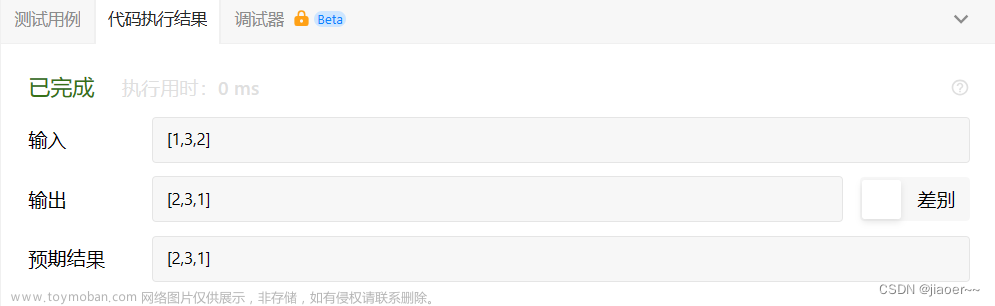
输入:nums = [1,1,1], k = 2
输出: 2
解释: 此题 [1,1] 与 [1,1] 为两种不同的情况

示例 2：

输入:nums = [1,2,3], k = 3
输出: 2

提示:

1 <= nums.length <= 2 * 104
1000 <= nums[i] <= 1000
107 <= k <= 107

解题思路

前置知识

前缀和

前缀和：顾名思义，是要求前缀的总和，什么是前缀，对于一个存放数字的数组而言，前缀就是指的数组的前k项，因此对应的前缀和就是数组前k项的和。前缀和一般用来求数组中连续段子数组的值的和，类似于等差数列中利用等差数列的和来求某一段子数列的和：

举个例子：

我们有一个数组nums = [2,4,6,1,4]

下面我们来计算nums数组的前缀和数组arr，arr[i] = arr[i-1] + nums[i]

第一个元素由于没有前缀所以只能是nums[0],也就是2

第二个元素就等于arr[1] = arr[0] + nums[1]

我们得到的nums的前缀和数组就为 arr = [2，6，12，13，17]

作用：

那么我们得到这个前缀和数组到底有什么用呢？

有了前缀和数组我们就可以方便的计算出，一个数组的区间之内的和，例如我们要求出nums[2]~nums[4] 的和。

nums[2]~nums[4] =nums[2] + nums[3] +nums[4] = arr[4] - arr[1] = 11

可以直接用前缀和数组中的两个元素求出，不用再进行相加操作。这样可以有效的减少我们的重复计算。

代码为：
    public int[] prefix(int[] nums) {
        int[] prefix = new int[nums.length];
        prefix[0] = nums[0];
        for (int i = 1; i < nums.length; ++i) {
            prefix[i] = prefix[i - 1] + nums[i];
        }
        return prefix;
 
    }

1.题目要求我们找到该数组中和为 k 的连续子数组的个数，我们可以先计算出数组的前缀和。

2.然后我们利用两个for循环遍历整个原数组，枚举求出各个区间的和，若和等于k，则answer加一，注意这里，如果区间为[0,n]时，也就是左区间为0时，区间和[0,n] 就等于 arr[n],这个情况比较特殊所以我们要单独计算。最后返回answer即可。

代码实现

class Solution {
    public int subarraySum(int[] nums, int k) {
        int[] sum = new int[nums.length];
        sum[0] = nums[0];
        for(int i = 1; i < nums.length; i++){
            sum[i] = sum[i-1] + nums[i];
        }
        int answer = 0;
        for(int i = 0; i < nums.length; i++){
            if(sum[i] == k){
                answer++;
            }
            for(int j = i + 1; j < nums.length; j++){
                if(  sum[j] - sum[i] == k){
                    answer ++;
                }
            }
        }

        return answer;
    }
}