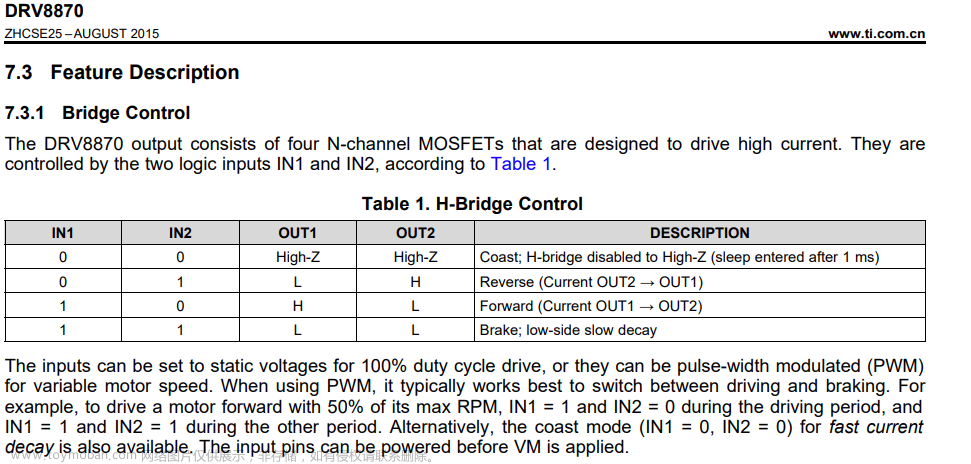
一、位式控制算法(引入PID)
只考察控制对象当前的状态值。

为了能够控制温度,速度等具有惯性性质的利用位式控制算法,框图如上。
以温度控制为例:图如下所示。
用户设定为SV,假设设定温度为80度,通过传感器将控制对象的温度PV进行获取。
(注:执行部件在此处可表示为加热器)
SV>PV时,位式控制算法输出H,加热器开始工作,温度上升。
SV≤PV时,位式控制算法输出L,加热器停止工作,温度慢慢下降。
位式控制算法也称为二位式控制算法,因为输出OUT只有H和L俩种情况,加热器也只有工作和不工作俩种情况。
由于控制对象是有一定的惯性的,当加热器由工作到不工作,水并不会温度立刻停止升温(还有一定的余温)来升温。
当加热器由不工作到工作状况时,水温不会立刻升温,加热器需要时候来升温,然后水开始升温。
核心思想:不断的将现在时刻,控制对象的值和用户设定的值进行比较,通过位式控制算法输出H或L来控制执行部件工作从而来达到和设定值一致的效果。

位式控制算法具有一定的局限性,只能考察当前的状态值,不会考虑其他的状态,会导致工作不平稳,只能满负荷或者停止工作。控制温度在设定范围内很难,于是引入PID算法来使得算法更精确\
二、PID算法:
为了使得控制更加精确引入了PID算法,主要利用偏差然后使用比例,积分,微分的思想来不断调整设定值和获取值之间的偏差。
P就是比例(proportional ) I就是积分(integral) D就是微分(derivative)
PID是三种不同的调节作用,可以使用一个或者多个。例如只使用P,使用P和I,使用P、I和D
| 以烧开水为例子:要烧水温度为50度,如果现在水温度和目标水温度相差不大加热器就“轻轻加热“、如果相差很大就”加足马力加热“ |
KP(比例):就让偏差(目标减去当前)与调节装置的“调节力度”,建立一个一次函数的关系,就可以实现最基本的“比例”控制了~ kP越大,调节作用越激进,kP调小会让调节作用更保守。
| 水温被加热到45度,但是散热和P加热作用一致,KD又觉得温度波动不大,不工作。于是需要KI来将45度和50度之间的误差进行一个积分后调节在P上,当水温到50度时KI调整完毕 |
KI(积分):I的作用就是,减小静态情况下的误差,让受控物理量尽可能接近目标值。
(使用I:需要设定积分限制。防止在刚开始加热时,就把积分量积得太大,难以控制,I越大,积分系数越大,效果越明显)
| 由于很多情况会使得水温在目标水温一直跳变,并且温差很大,于是利用KD,当水温和目标水温相差很小时候,阻止KP的作用,使得水温不变化。于是可以将水温稳定在一个温度左右。 |
KD(微分):当比较接近目标时,P的控制作用就比较小了。越接近目标,P的作用越温柔。有很多内在的或者外部的因素,使控制量发生小范围的摆动。D的作用就是让物理量的速度趋于0,只要什么时候,这个量具有了速度,D就向相反的方向用力,尽力刹住这个变化
(KD相当于是调整KP的抖动问题,阻止KP带来装置抖动,KD越大,防止的力道就越强)

框图中将P,I,D三个部分理解成存储器,将计算出的偏差数据存储在这里。
通过传感器不断读取负载的状态值得到一个数据数列:𝑋1、𝑋2、𝑋3…. 𝑋k−2、𝑋k−1、𝑋k =Pv
通过计算偏差得到历史偏差数据数列:𝐸1、𝐸2、𝐸3…. 𝐸k−2、𝐸k−1、𝐸k会有三种情况

其OUT输出不只是位式控制算法只有H和L,而是输出PWM信号(控制电压有效值)从而控制工作的功率可以改变
速度就是:当速度超过目标值就降低PWM中占空比从而降低速度,当速度值小于目标值就提高PWM占空比提高速度
| 例如设定距离为100m,最开始的时候速度为0,所以err=目标值-实际值=100,通过KP乘以100转化为一定的速度例如50m/s 运行一定时间后则距离减小,则err减小,则速度不断减小,等到到100m处后err=0则速度为0,实现pid的控制过程 |
通过𝐸k乘上一个系数Kp 输出OUT,即OUT1=𝐸k∗Kp。
当;目标值和传感器获取值𝐸k较大,则OUT较大来调整负载,𝐸k偏差很小时则OUT也很小,负载无需很大调整。
(Kp表示放大或缩小的系数,也是我们应该调的P的大小)
比例控制就是当前偏差值比例大小输出控制信号OUT来控制PWM的占空比
缺点:当𝐸k=0时,输出PWM=0,负载会处于停止状态,处于失控状态,由于空气流动等原因容易产生震荡
为了防止系统出现失控,如果只单独使用P算法可以加一个OUT0
I:积分( 离散化便是求和 与历史偏差有关𝐸1、𝐸2、𝐸3…. 𝐸k−2、𝐸k−1、𝐸k)
将历史偏差求代数和后,𝑆k=𝐸1+𝐸2+𝐸3…. 𝐸k−2+𝐸k−1+𝐸k也会出现三种情况,即大于0、等于0、小于0

通过𝑆k乘上Ki来放大输出OUT,即OUT2=𝑆k∗Ki
缺点:只考虑过去的时间,并没有很好的考虑到当前的状态,历史的状态会很影响当前的状态。
把问题控制在没有发生之前,而不是问题发生了才开始控制,往往来不及
在PID调试中,I是最后进行调整的,因为最复杂,涉及到了历史过去的众多状态。(是为了消除静态误差)
D:微分(与最近偏差有关𝐸k−1、𝐸k,涉及到未来的趋势)

𝐷k =0:例如取样三次温度为70,72,74.目标温度为80则利用公式𝐸k−1=2=𝐸k,于是𝐷k =0。
但是实际温度并没有达到目标温度,于是还需要其I来考察历史偏差累加后进行修正,所以D不能独立行动,最少和P一起配合来调整,D来抑制P的偏差变化趋势。
对于变化趋势很有可能是延续到未来的时刻的,利用偏差之差来控制输出
通过Kd可以改变其斜率的大小从而改变其趋势的程度,控制其灵敏度。(D是抑制P的)
微分算法只关心其偏差有没有变化趋势,而不是考察偏差是否存在
积分和微分都是和时间相关的,但是为了简单将时间t设置为单位时间,微分其变化是偏差的变化率。
于是为了系统的多方面考虑,需要结合三者的优缺点从而一起调整系统从而达到我们预期的效果。
PID调参效果演示:

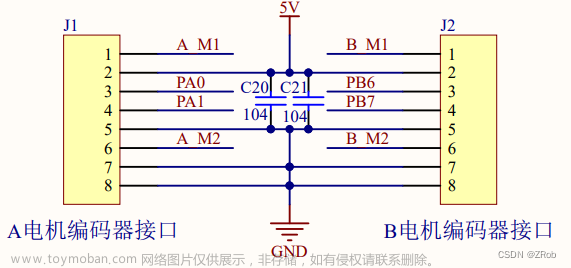
霍尔编码器:
定时器具有特殊的编码器接口来方便的计算转速的大小。
编码器模式下,计数器的计数方向代表的电机的正转与反转,计数的大小代表了转速的大小。
如图:利用俩个脉冲之间的关系来判断是正转还是反转,通过极性的设置可以改变其计数的方向。
编码器有俩路正交的输入信号,理论一个周期捕获一个信号,俩个信号正交90度,通过捕获俩个信号上下边缘,可以在一个周期捕获四个信号 达到四倍频的效果。(捕获到是累计的脉冲数)以边沿和电平的关系当正转或者反转时的关系来更好的理解计数过程。
测速方法:M法(频率测量法,适用高速)
在固定计数周期,统计该段时间内编码器脉冲数,计算速度值

n为计算出的电机转速
C编码器单圈总脉冲数
T0为时间段
M0为在时间T0内统计到的编码器脉冲数
加入单圈编码器脉冲数为2000个,在1.5s内统计到脉冲数为3000个,通过公式计算可以得到,转速为1圈/s
T法(周期测量法,适用低速)
建立已知频率高频脉冲对其计数,计数时间为编码器相邻俩个脉冲间隔时间Te,计数值为M1。编码器单圈总脉冲数为C,已知高频频率为F0则

M/T法(综合M法和T法优势)
既测量编码器脉冲数也测量一定时间内高频脉冲数。在一固定时间内,计数编码器脉冲数为M0,计数已知频率为F0的高频脉冲,计数值为M1,编码器单圈脉冲数为C则

PID代码过程:
1、主要利用定时器输出PWM波来控制电机的速率
2、利用输入捕获来获取当前霍尔编码器的数据,其中定时器有特定的函数来满足编码器的使用。需要函数计算当前的速度。(在TIM.h库中)

3、利用串口助手来调试其中PID的参数,可以利用vofa软件来看波形,还需要设置串口来调节P,I,D的值而不是每次需要编译代码后下载。
4、主要的PID的公式计算。
5、对于PWM和霍尔编码器需要进行一个联合。
(多用函数和宏定义来封装函数)
还未加霍尔编码器让电机转动,不需要将电机pwm函数加入到循环里面一直去执行,因为并没有时刻的去改变速度值,如果需要不断的去读取霍尔编码器的值然后设定速度值就需要加入循环中去执行
PID调参环节:
1、试凑法:根据设计的系统选择合适的采样周期,多次试凑,选择性能较好的一个作为采样周期。先只使用P,从小到大调整,I和D也是如此操作调节到理想的曲线即可

2、临界比例法:将调节器置于纯比例的作用下,从大到小逐渐改变调节器的比例度,得到等幅度的震荡过程叫临界比例度。
3、一般调节法:
针对一般的PID控制系统
a.在输出不振荡时,增大比例系数P。
b.在输出不振荡时,减小积分系数Ki。
c.在输出不振荡时,增大微分系数Kd。
(他们三个任何谁过大都会造成系统的震荡)

PID调节的采样周期如何选择:
选择好采样周期才能更好的判断电机的旋转方向、计算速度等信息
PID调参口诀:

使用MG310电机来进行PID的对象

1、利用定时器产生PWM驱动电机转动
2、使用串口更好的观察PID调参过程,下发指令
3、使用定时器获取霍尔编码器的数据并且计算其电机现在的速度
4、编写PID公式,计算其PID计算过程
5、配置PWM来控制电机正反转
6、主函数初始化、延时函数库。文章来源:https://www.toymoban.com/news/detail-607287.html
.........代码更新整理中文章来源地址https://www.toymoban.com/news/detail-607287.html
到了这里,关于PID理论基础及代码详解【stm32标准库】的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!