熵权法是根据评价指标的变异程度（差异系数）来分配权重，评价指标变异程度越大，所赋权重就越大，并以此对评价对象进行综合评价的方法
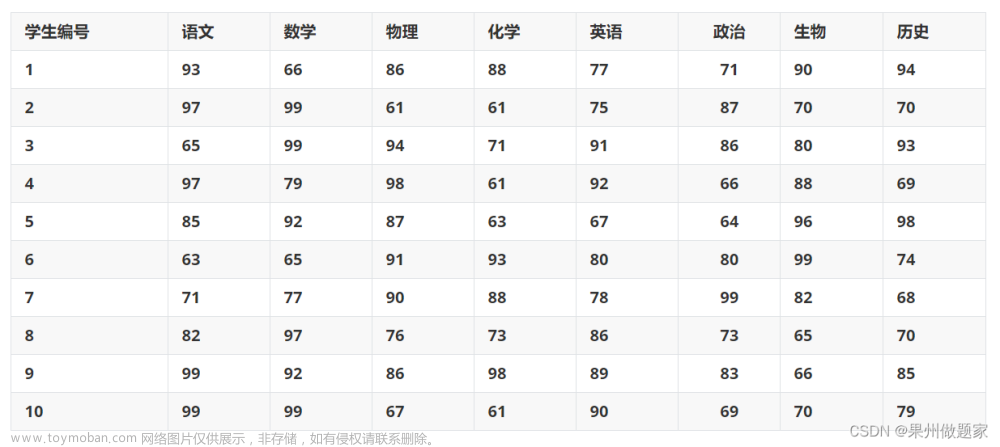
第一步 导入第三方库和案例数据
import numpy as np
import pandas as pd
#按指定路径导入数据，以“地区”为索引（文件路径需按实际情况更换）
data = pd.read_excel(r'C:/Users/AROUS/Desktop/综合评价数据.xlsx', index_col = '地区')
data
第二步 标准化数据（min-max标准化）
使用min-max标准化方法标准化数据后，各评价指标的最大值为1，最小值为0
正向指标（指标值越大越好）的min-max标准化计算公式为：
y i j = x i j − min x i j max x i j − min x i j ( 1 ≤ i ≤ n , 1 ≤ j ≤ m ) y_{ij} = \frac{x_{ij} - \min{x_{ij}}}{\max{x_{ij}} - \min{x_{ij}}} \quad (1 \leq i \leq n,1 \leq j \leq m) yij=maxxij−minxijxij−minxij(1≤i≤n,1≤j≤m)， n n n为评价对象的个数， m m m为评价指标的个数
负向指标（指标值越小越好）的min-max标准化计算公式为：
y i j = max x i j − x i j max x i j − min x i j ( 1 ≤ i ≤ n , , 1 ≤ j ≤ m ) y_{ij} = \frac{\max{x_{ij}} - x_{ij}}{\max{x_{ij}} - \min{x_{ij}}} \quad (1 \leq i \leq n, , 1 \leq j \leq m) yij=maxxij−minxijmaxxij−xij(1≤i≤n,,1≤j≤m)， n n n为评价对象的个数， m m m为评价指标的个数
#定义正向指标min-max标准化函数
def minmax_p(x):
return (x - x.min()) / (x.max() - x.min())
#定义负向指标min-max标准化函数
def minmax_n(x):
return (x.max() - x) / (x.max() - x.min())
#使用正向指标min-max标准化函数标准化数据
data_m = data.apply(minmax_p, axis = 0)
data_m
第三步 计算评价指标的特征比重
第 i i i个评价对象的第 j j j项评价指标的特征比重的计算公式为：
p i j = y i j ∑ i = 1 n y i j p_{ij} = \frac{y_{ij}}{\sum_{i=1}^{n} y_{ij}} pij=∑i=1nyijyij， n n n为评价对象的个数
pij = data_m / data_m.sum()
pij
第四步 计算评价指标的熵值
第 j j j项评价指标的熵值的计算公式为：
e j = − 1 ln ( n ) ∑ i = 1 n p i j ln ( p i j ) e_j = -\frac{1}{\ln(n)} \sum_{i=1}^{n} p_{ij} \ln(p_{ij}) ej=−ln(n)1∑i=1npijln(pij)， n n n为评价对象的个数
#把pij中的0替换为一个非零的极小值，避免出现ln(0)的警告
#函数len用于返回对象的长度或元素个数
pij = pij.replace(0, 1e-100)
ei = -1 / np.log(len(data_m)) * np.sum(pij * np.log(pij), axis = 0)
ei
第五步 计算评价指标的差异系数
第 j j j项评价指标的差异系数的计算公式为：
d j = 1 − e j d_j = 1 - e_j dj=1−ej
di = 1 - ei
di
第六步 计算评价指标的权重
#归一化评价指标的差异系数
w = di / di.sum()
w
文章来源：https://www.toymoban.com/news/detail-607607.html
第七步 计算评价对象的综合得分
data['熵权法得分'] = data_m.dot(w)
data
文章来源地址https://www.toymoban.com/news/detail-607607.html
第八步 导出综合评价结果
data.to_excel('熵权法综合评价结果.xlsx', index = True)
下期预告： P y t h o n 综合评价模型（九） C R I T I C 法 \textcolor{RoyalBlue}{下期预告 ： Python综合评价模型（九）CRITIC法} 下期预告：Python综合评价模型（九）CRITIC法
关注公众号“ T r i H u b 数研社”发送“ 230402 ”获取案例数据和代码 \textcolor{RoyalBlue}{关注公众号“TriHub数研社”发送“230402”获取案例数据和代码} 关注公众号“TriHub数研社”发送“230402”获取案例数据和代码
到了这里，关于Python综合评价模型（八）熵权法的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
