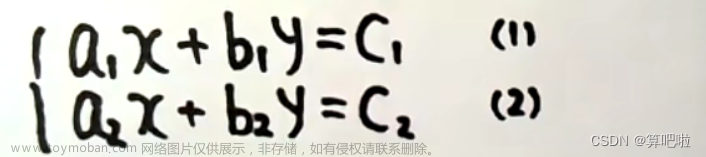数值线性代数：知识框架

7月前作者：JiNan.YouQuan.Soft 分类：Toy博客阅读(28) 违法举报

这篇具有很好参考价值的文章主要介绍了数值线性代数：知识框架。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

记录数值线性代数研究的知识框架。

			软件包
线性方程组	直接法	Guass消元法/LU分解、Cholesky分解	LAPACK oneAPI MKL ARPACK Octave
线性方程组	迭代法	Jacobi迭代、SOR迭代、共轭梯度法
最小二乘
特征值/特征向量	非对称	幂法、QR、Arnoldi分解
特征值/特征向量	对称	QR、Jacobi、二分法、分治法、SVD

参考书籍

Golub G H , Loan C F V .Matrix Computations.Johns Hopkins University Press,1996.

Ford W .Numerical Linear Algebra with Applications using MATLAB. 2014.

徐树方. 数值线性代数(第二版). 北京大学出版社, 2010.

网络资料

LAPACKhttps://www.netlib.org/lapack/index.html

Intel oneAPI MKLhttps://www.intel.com/content/www/us/en/developer/tools/oneapi/onemkl.html

LAPACKhttps://github.com/opencollab/arpack-ng.git

Octavehttps://www.octave.org/文章来源地址https://www.toymoban.com/news/detail-608056.html

到了这里，关于数值线性代数：知识框架的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：如若内容造成侵权/违法违规/事实不符，请点击违法举报进行投诉反馈，一经查实，立即删除！

分享到：

领支付宝红包赞助服务器费用

MATLAB数值分析学习笔记：线性代数方程组的求解和高斯消元法

工程和科学计算的许多基本方程都是建立在守恒定律的基础之上的，比如质量守恒等，在数学上，可以建立起形如 [A]{x}={b} 的平衡方程。其中{x}表示各个分量在平衡时的取值，它们表示系统的状态或响应；右端向量{b}由无关系统性态的常数组成通常表示为外部激励。矩阵

2023年04月15日
浏览(50)
MATLAB数值分析学习笔记：线性代数方程组的求解和高斯-赛德尔方法

迭代法是前面介绍的消元法的有效替代，线性代数方程组常用的迭代法有高斯-赛德尔方法和雅克比迭代法，下面会讲到二者的不同之处，大家会发现两者的实现原理其实类似，只是方法不同，本篇只重点介绍高斯-赛德尔方法。看了我之前的笔记的同学应该已经对迭代法不

2024年02月05日
浏览(43)
线性代数的学习和整理2：线性代数的基础知识(整理ing)

目录 1 写在前面的话 1.1 为什么要先总结一些EXCEL计算矩阵的工具性知识，而不是一开始就从基础学起呢？ 1.2 关于线性代数入门时的各种灵魂发问： 1.3 学习资料 2 什么是线性(关系)？ 2.1 线性的到底是一种什么关系：线性关系=正比例/正相关关系 ≠ 直线型关系 2.2 一次函数

2024年02月14日
浏览(52)
线性代数基础知识

计算机视觉一些算法中常会用到线性代数的一些知识，为了便于理解和快速回忆，博主这边对常用的一些知识点做下整理，主要来源于如下这本书籍。 1. 矩阵不仅仅是数字排列而已，不然也不会有那么大精力研究它。其可以表示一种映射关于映射，变换的一些帖子可以参

2024年02月03日
浏览(41)
线性代数知识

❀关于李永乐-线性代数基础班学习笔记。 1.1.1 二、三阶行列式若有二元一次方程组，进行加减消元：根据相加相减的系数，可以提炼成二阶行列式假设方程组系数行列式不为0，则可让分母做运算。若解三元一次方程组，很自然会出现3个数加加减减。注意只有二三阶才可

2024年02月04日
浏览(33)
【数值计算方法（黄明游）】解线性代数方程组的迭代法（一）：向量、矩阵范数与谱半径【理论到程序】

注意：速读可直接跳转至“4、知识点总结”及“5、计算例题”部分当涉及到线性代数和矩阵理论时，向量、矩阵范数以及谱半径是非常重要的概念，下面将详细介绍这些内容： a. 定义及性质考虑一个 n n n 维向量 x x x ，定义一个实值函数 N ( x ) N(x) N ( x ) ，

2024年01月25日
浏览(34)
线性代数入门：基础知识与实践

线性代数是数学的一个分支，主要研究的是线性方程组和向量空间等概念。它在现代科学和工程领域中具有广泛的应用，如计算机图形学、机器学习、信号处理、金融等。线性代数的核心内容包括向量、矩阵、线性方程组的求解、向量空间等。在本文中，我们将从线性代数的

2024年02月22日
浏览(42)
线性代数-知识点复习（面试用）

整理：Peter1146717850 一、向量与线性组合向量：往什么方向走多么远 e.g. ( 1 2 ) begin{pmatrix} 1 \\\\ 2end{pmatrix} ( 1 2 ) 向量的模：向量的长度向量的加减法：向量对应元素相加减（前提：维度相同） ( a b c ) + ( x y z ) = ( a + x b + y c + z ) begin{pmatrix} a \\\\b \\\\ cend{pmatrix} + begin{pma

2024年04月25日
浏览(25)
深度学习-必备的数学知识-线性代数5

线性代数在数学中，分解通常指的是将一个复杂的对象或结构分解为更简单的部件或组件。这个概念在许多数学领域都有应用。在线性代数中，矩阵分解是常见的一个主题，我们通过分解矩阵来发现它不明显的性质。矩阵有许多种的分解方式：LU分解、QR分解、特征分解、奇

2024年02月02日
浏览(55)
深度学习-必备的数学知识-线性代数（合集）

为方便大家阅读，这里推出一个线性代数的合集。这与之前的内容是一致的。我们在深度学习-简介和深度学习-历史背景中已经初步了解的深度学习。在我们开始学习深度学习前还需要做些准备工作。就是学习应用数学和机器学习基础。想要理解深度学习这些是必不可少的

2024年02月03日
浏览(35)