区间预测 | MATLAB实现QRLSTM长短期记忆神经网络分位数回归多输入单输出区间预测
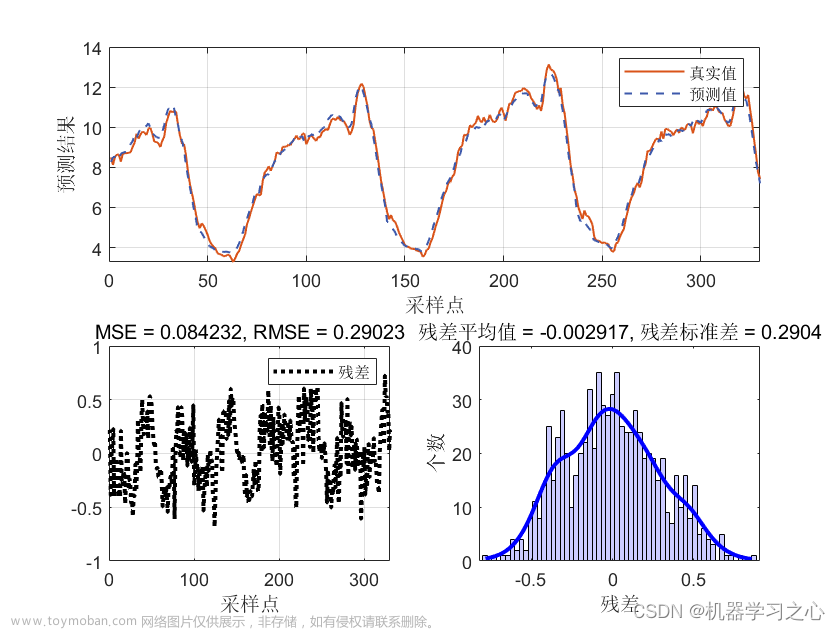
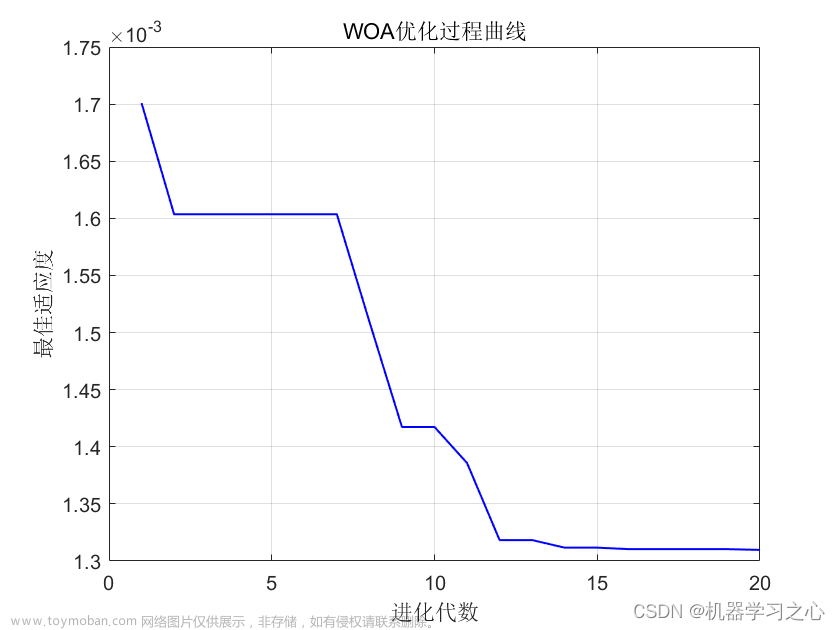
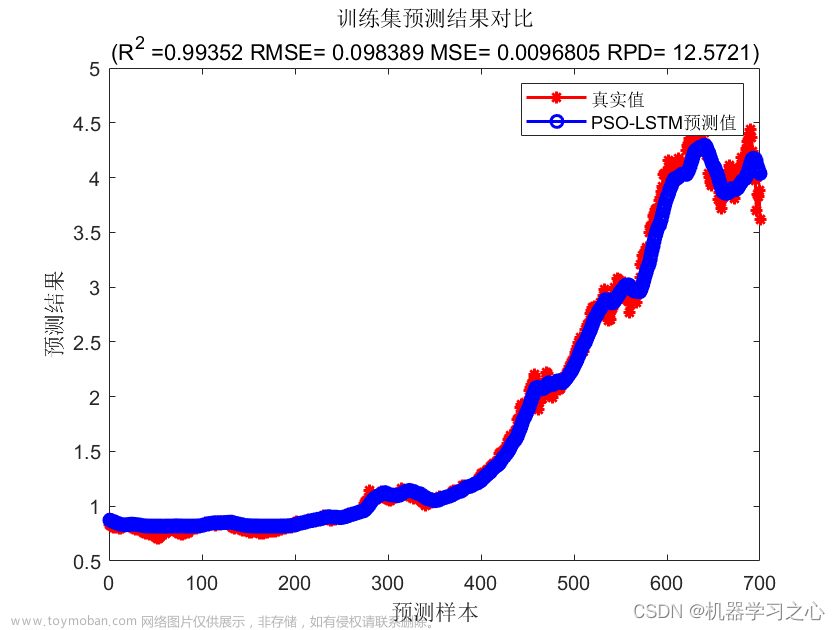
效果一览




基本介绍
MATLAB实现QRLSTM长短期记忆神经网络分位数回归时间序列区间预测
QRLSTM是一种基于长短期记忆(LSTM)神经网络的模型,用于时间序列区间预测。它是使用分位数回归来进行预测的,这意味着它可以预测一系列可能的结果,而不仅仅是单个点预测。
具体来说,QRLSTM使用LSTM网络来学习时间序列的长期和短期依赖关系,然后使用分位数回归来预测一系列可能的结果。分位数回归是一种非常有用的技术,它可以预测出给定置信水平下的上限和下限,这对于时间序列预测非常有用。
QRLSTM模型的预测能力很强,特别是在处理非线性时间序列时。它已经被广泛应用于股票市场、气象预测、交通预测等领域。
模型描述
QRLSTM模型的数学公式如下:
首先,我们定义LSTM网络中的隐藏状态和细胞状态:
h t , c t = LSTM ( x t , h t − 1 , c t − 1 ) h_t,c_t=\text{LSTM}(x_t,h_{t-1},c_{t-1}) ht,ct=LSTM(xt,ht−1,ct−1)
- 其中, x t x_t xt是时间步 t t t的输入, h t − 1 h_{t-1} ht−1和 c t − 1 c_{t-1} ct−1分别是上一时间步的隐藏状态和细胞状态。
然后,我们定义分位数回归的损失函数:
L τ = ∑ i = 1 n ρ τ ( y i − f θ ( x i ) ) \mathcal{L}{\tau}=\sum{i=1}^{n}\rho_{\tau}(y_i-f_{\theta}(x_i)) Lτ=∑i=1nρτ(yi−fθ(xi))
- 其中, τ \tau τ是分位数水平, y i y_i yi是时间序列在时间步 i i i的真实值, f θ ( x i ) f_{\theta}(x_i) fθ(xi)是模型在时间步 i i i的预测值, ρ τ ( u ) \rho_{\tau}(u) ρτ(u)是分位数损失函数:
ρ τ ( u ) = { τ u if u ≥ 0 ( τ − 1 ) u if u < 0 \rho_{\tau}(u)=\begin{cases} \tau u & \text{ if } u \geq 0 \ (\tau-1)u & \text{ if } u < 0 \end{cases} ρτ(u)={τu if u≥0 (τ−1)u if u<0
最终我们的目标是最小化所有分位数水平下的损失函数:
L = ∑ τ ∈ τ 1 , τ 2 , . . . , τ T L τ \mathcal{L}=\sum_{\tau\in{\tau_1,\tau_2,...,\tau_T}}\mathcal{L}_{\tau} L=τ∈τ1,τ2,...,τT∑Lτ
- 其中, τ 1 , τ 2 , . . . , τ T {\tau_1,\tau_2,...,\tau_T} τ1,τ2,...,τT是一组分位数水平。
QRLSTM模型使用随机梯度下降或者其他优化算法最小化上述损失函数,从而得到最优的模型参数。文章来源:https://www.toymoban.com/news/detail-608719.html
程序设计
- 完整程序和数据获取方式1,订阅《LSTM长短期记忆神经网络》(数据订阅后私信我获取):MATLAB实现QRLSTM长短期记忆神经网络分位数回归多输入单输出区间预测,专栏外只能获取该程序。
- 完整程序和数据获取方式2,(资源出下载):MATLAB实现QRLSTM长短期记忆神经网络分位数回归多输入单输出区间预测
% 构建模型
numFeatures = size(XTrain,1); % 输入特征数
numHiddenUnits = 200; % 隐藏单元数
numQuantiles = 1; % 分位数数目
layers = [ ...
sequenceInputLayer(numFeatures)
lstmLayer(numHiddenUnits,'OutputMode','last')
dropoutLayer(0.2)
fullyConnectedLayer(numQuantiles)
regressionLayer];
options = trainingOptions('adam', ...
'MaxEpochs',50, ...
'MiniBatchSize',64, ...
'GradientThreshold',1, ...
'Shuffle','every-epoch', ...
'Verbose',false);
net = trainNetwork(XTrain,YTrain,layers,options); % 训练模型
% 测试模型
YPred = predict(net,XTest); % 预测输出
quantiles = [0.1,0.5,0.9]; % 分位数
for i = 1:length(quantiles)
q = quantiles(i);
epsilon = YTest - YPred(:,i); % 预测误差
lag = 10; % 滞后期数
sigma = median(abs(epsilon(max(1,end-lag+1):end))) * 1.483; % 置信区间
lb = YPred(:,i) - sigma * norminv(1-q/2,0,1); % 置信区间下限
ub = YPred(:,i) + sigma * norminv(1-q/2,0,1); % 置信区间上限
disp(['Quantile:',num2str(q),' MAE:',num2str(mean(abs(epsilon))),' Width:',num2str(mean(ub-lb))]);
end
参考资料
[1] https://blog.csdn.net/kjm13182345320/article/details/127931217
[2] https://blog.csdn.net/kjm13182345320/article/details/127418340文章来源地址https://www.toymoban.com/news/detail-608719.html
到了这里,关于区间预测 | MATLAB实现QRLSTM长短期记忆神经网络分位数回归多输入单输出区间预测的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!