一、二叉树的结构
二叉树的节点结构如下所示
template<typename T>
struct TreeNode
{
T data; //数据
TreeNode* left; //指向左孩子节点的指针
TreeNode* right; //指向右孩子节点的指针
TreeNode(T dat, TreeNode* lft = nullptr, TreeNode* rig = nullptr):data(dat), left(lft), right(rig) {}
};如下所示是一个二叉树,其中的每一个节点都是由上述TreeNode节点的一个具体对象。

二、先序遍历、中序遍历、后序遍历
1、什么是先序遍历
先遍历根(父)节点、再遍历左节点、最后遍历右节点。
注意:这里说的遍历并不是行走。毕竟我们能够先取到的指针只有根节点指针,而如果想找一个节点,则一定要先找到它的根节点。这里的遍历指的是“介绍”这棵树的方式。通常来讲,我们是使用的打印的方式“介绍”一棵树的。
所以,先序遍历展开来讲是:如果一棵树上有根节点,则先输出根节点,再输出左孩子节点、最后输出右孩子节点。
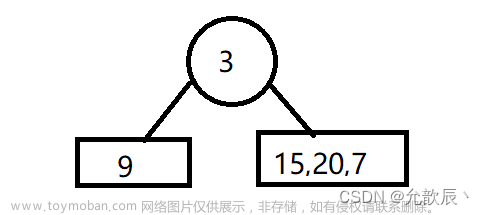
例如,上述图1中的二叉树,先序遍历输出是:3、9、20、15、7
2、什么是中序遍历
先遍历输出左孩子节点,再遍历输出根节点,最后遍历输出右孩子节点。
例如,上述图1中的二叉树,中序遍历输出是:9、3、15、20、7
3、什么是后序遍历
先遍历输出左孩子节点,再遍历输出右孩子节点,最后遍历输出根节点。
例如,上述图1中的二叉树,后序遍历输出是:9、15、7、20、3
三、三种遍历的递归法
1、二叉树的递归序
首先,我们逐步分析二叉树的递归原理。我们取一个临时指针temp,来在二叉树上行进(根-左-右的顺序),则temp的指向顺序、即二叉树的递归序是:
--START
3(根节点)
9(找到3的左孩子、左子树根节点)
9(找9的左孩子,没有,则回到9)
9(找9的右孩子,没有,则回到9)
3(3的左子树遍历完毕,回到3)
20(3的右子树根节点)
15(20的左孩子)
15(15的左孩子,没有,回到15)
15(15的右孩子,没有,回到15)
20(20的左子树遍历完毕,回到20)
7(20的右孩子)
7(7的左孩子,没有,回到7)
7(7的右孩子,没有,回到7)
20(20的右子树遍历完毕,回到20)
3(3的右子树遍历完毕,回到3)
--END
其中的temp指向其实指的是
上述过程用代码实现如下:
void traversal(TreeNode* root) {
//1)程序资源在root节点,判空
if (nullptr == root)
{
return;
}
//2)遍历左子树
traversal(root->left);
//左子树遍历完成,程序资源回到root节点
//3)遍历右子树
traversal(root->right);
//右子树遍历完成,程序资源回到root节点
return;
}2、三种遍历的递归法实现
则我们可以看见规律。二叉树的递归序中,每一个节点都会被遍历3次。每个节点,当其作为root节点、左子树遍历完成、右子树遍历完成的时候,程序资源都会回到这个节点。
1)先序遍历的递归法
而先序遍历,则只要在第一次处于这个节点的时候进行输出即可。见下列代码:
void preorderTraversal(TreeNode* root) {
//根节点为空,直接返回
if (nullptr == root)
{
return;
}
//1)输出
cout << root->val << endl;
//2)遍历左子树
preorderTraversal(root->left);
//3)遍历右子树
preorderTraversal(root->right);
return;
}2)中序遍历的递归法
同理,中序遍历,只要在递归序的基础上,在第二次回到节点时输出即可。见下列代码:
void inorderTraversal(TreeNode* root) {
//根节点为空,直接返回
if (nullptr == root)
{
return;
}
//1)遍历左子树
inorderTraversal(root->left);
//2)输出
cout << root->val << endl;
//3)遍历右子树
inorderTraversal(root->right);
return;
}3)后序遍历的递归法
同理,后序遍历,只要在递归序的基础上,在第三次回到节点时输出即可。见下列代码:
void postorderTraversal(TreeNode* root) {
//根节点为空,直接返回
if (nullptr == root)
{
return;
}
//1)遍历左子树
postorderTraversal(root->left);
//2)遍历右子树
postorderTraversal(root->right);
//3)输出
cout << root->val << endl;
return;
}这样理解,二叉树的递归遍历法是不是非常简单了?
四、三种遍历的非递归法
任何递归函数都可以改成非递归函数。我们使用的递归法,其实是系统帮助我们压栈的一个过程。
1、分析解决方案
我们知道栈的特性是先入后出,如果按照一般遍历顺序根节点-左孩子-右孩子进行压栈,则和上述遍历顺序不符
2、三种遍历的非递归实现
1)先序遍历实现
算法步骤:
a、根节点进栈;
b、弹出并输出栈顶节点tp;
c、栈顶节点tp的左孩子进栈、右孩子进栈;
d、重复上述b、c;
代码实现:文章来源地址https://www.toymoban.com/news/detail-608766.html
void preorderTraversal(TreeNode* root) {
if (nullptr == root)
{
return;
}
stack< TreeNode*> mstack;
mstack.push(root);
while (!mstack.empty())
{
//打印栈顶节点
TreeNode* tp = mstack.top();
cout << tp->val << endl;
//弹出节点
mstack.pop();
//右孩子节点压栈
if (nullptr != tp->right)
{
mstack.push(tp->right);
}
//左孩子节点压栈
if (nullptr != tp->left)
{
mstack.push(tp->left);
}
}
return;
}
2)中序遍历实现
算法步骤:
a、从根节点开始,整棵树的左边界节点依次进栈;
b、弹出并输出栈顶节点tp;
c、栈顶节点tp的右子树左边界节点依次进栈;
d、重复上述b、c;
代码实现:
void inorderTraversal(TreeNode* root) {
TreeNode* tp = root;
stack< TreeNode*> mstack;
//弹出并输出栈顶节点,并对其右孩子节点压栈
while (!mstack.empty() || nullptr != tp)
{
//左边界节点依次进栈
if (nullptr != tp)
{
mstack.push(tp);
tp = tp->left;
}
else
{
//获取栈顶节点指针
tp = mstack.top();
//输出
cout << tp->val << endl;
//弹出节点
mstack.pop();
//如果有右子树,右子树的左边界节点压栈
tp = tp->right;
}
}
return;
}3)后序遍历实现
后序遍历即:左-右-根 的顺序。一般来说,我们一定会先行进到根节点,才能找到其左右子树。所以,我们可以想办法获得 根-右-左的节点遍历,再利用栈的特性反序输出。
算法步骤:
申请两个栈,s1,s2
a、根节点入栈s1;
b、弹出(不输出)栈顶节点tp,压入栈s2;
c、栈顶节点tp的左孩子、右孩子依次进栈s1;
d、重复上述b、c,直到栈s1为空,所有节点进入栈s2;
e、依次弹出并输出栈s2栈顶节点;文章来源:https://www.toymoban.com/news/detail-608766.html
代码实现:
void postorderTraversal(TreeNode* root) {
//根节点为空,直接返回
if (nullptr == root)
{
return;
}
//申请2个栈
stack< TreeNode*> s1, s2;
//根节点压入s1
s1.push(root);
while (!s1.empty())
{
TreeNode* tp = s1.top();
s2.push(tp);
s1.pop();
if (nullptr != tp->left)
{
s1.push(tp->left);
}
if (nullptr != tp->right)
{
s1.push(tp->right);
}
}
//依次弹出并输出s2节点
while (!s2.empty())
{
cout << s2.top()->val << endl;
s2.pop();
}
return;
}到了这里,关于二叉树的先序、中序、后序遍历C++的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!