力扣[24、19、面试题02.07、142]

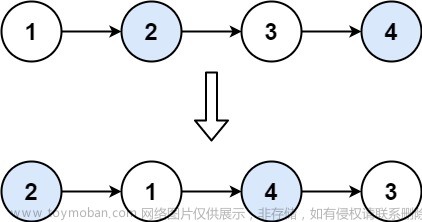
24. 两两交换链表中的节点

题目链接：

解题思路：

递归：自己的

1. 两两交换两个节点，也就是说是成对的交换！每次交换两个，下一次交换的时候，就要从第三个开始。
2. 然后如上图可以看出来：我们可以将链表分为三个部分，已经交换的部分，和接下来准备交换的两个节点！
3. 那么不难想到递归，递归处理两个交换的节点，每级递归都是在做同样的事情！
4. 递归的终止条件：当没有节点交换的时候不就终止了吗，但是要考虑奇数的问题，假设现在有3个节点，1、2两个节点已经完成了交换，现在跳转到第三个节点了，那么发现第三个节点的下一个节点是空节点，所以说终止，只需要判断一下即可，因为奇数的话，前面两两交换，必然有一个落单！终止条件：当前节点为空，或当前节点的下一个节点为空；
5. 递归的返回值：返回的是头节点，即已经处理好的链表的头节点，每次递归的时候，都将当前交换的两个节点的前驱节点作为头节点，进行交换，那么返回的时候也是返回当前的前驱节点，即为头节点！
6. 一级递归的任务：交换两个节点的指向的前提是后面的节点不会丢失。所以说先保留第二个节点，然后将第一个节点的指针指向第三个节点，最后将第二个节点的指针指向第一个节点，即交换完毕！

实现代码：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* swapPairs(ListNode* head) {
        if (head == nullptr || head->next == nullptr) {
            return head;
        }

        ListNode* cur = head->next;
        head->next = swapPairs(head->next->next);
        cur->next = head;
        return cur;     //此时cur才是头节点！
    }
};

复杂度分析：

我们来分析其时间复杂度：

由于在每次递归调用中，我们都会移动到链表的下一个节点，所以我们会遍历整个链表一次。这意味着这个函数的时间复杂度是O(n)，其中n是链表中节点的数量。

空间复杂度方面，由于这是一个递归函数，因此递归调用会在调用栈中占用空间。在最坏的情况下，如果链表中有n个节点，那么我们需要进行n次递归调用，因此空间复杂度也是O(n)。

虚拟头节点：别人的

1. 设置一个虚拟头节点，通过循环两两节点进行交换！
2. 当虚拟头节点之后的两个节点一个为空，则停止循环。也就是说虚拟头节点每次只移动两步。指向的是即将交换的两个节点的前一个节点。
3. 那么交换的操作是：定义两个临时指针，记录交换的两个节点的前面的那个节点，另一个指针记录的交换节点的后面的那个节点的下一个节点！然后利用cur进行操作，先让cur节点的指针指向第节点2，再让节点2的指针指向节点1，最后让节点1的指针指向节点2的后面的节点。
4. 最后让cur指针移动到交换后的节点的上面，方便对后续进行同样的操作！

实现代码：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* swapPairs(ListNode* head) {
        ListNode* dummyHead = new ListNode(0);
        dummyHead->next = head;
        ListNode* cur = dummyHead;

        while (cur->next != nullptr && cur->next->next != nullptr)
        {
            ListNode* tmp1 = cur->next;
            ListNode* tmp2 = cur->next->next->next;

            cur->next = cur->next->next;
            cur->next->next = tmp1; 
            cur->next->next->next = tmp2;

            cur = cur->next->next;
        }
        return dummyHead->next;
    }
};

复杂度分析：

该算法的工作原理是，迭代遍历链表，每次取两个节点，并进行交换。

现在让我们分析时间复杂度和空间复杂度：

时间复杂度：对于这个算法，我们需要遍历所有的节点，所以时间复杂度为O(n)，其中n为链表的长度。

空间复杂度：我们只使用了固定的额外空间，所以空间复杂度为O(1)。

总的来说，这个算法在时间和空间上都非常高效。

题目总结：

画图！

19. 删除链表的倒数第N个节点

题目链接：

解题思路：

正数第x个节点：自己的

给定的是倒数第n个节点，那么我们需要锁定的是倒数第n个节点的前一个节点，以此方便我们好删除。但是如何找到倒数第n个节点呢？大家都知道，遍历一个链表都是从头开始遍历，是正着的，而不是反着遍历的，所以说我们应该将倒数第n个节点转化为正数第xxx个节点。

数学规律：5个节点，现在要删除其倒数第2个节点，那么该节点应该是正数的第（5-2 + 1）个节点，即第4个节点。

通用：假如总节点数为n，给定你倒数第x个节点，那么它是正数的第（n-x+1）个节点。

所以问题来了，给定我们一个链表我们怎么知道链表的节点数一共有多少个呢？
显然只有先遍历一遍，定义一个计数器！

所以说此方法分为两个步骤：
1、先计算节点总数
2、找第正数第（n-x+1）个节点！

但是删除第（n-x+1）个节点的话，需要找它的前一个节点，所以说是找第（n-x）个节点！所以我们的目标是找删除节点的前一个节点

此外还需要考虑删除头节点的情况：即此时的倒数第n个节点，实际上就是第一个节点的时候。

实现代码：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        //考虑只有一个节点的情况！
        
        int cnt=0;
        ListNode* cur = head;

        while (cur != nullptr)
        {
            cnt ++;
            cur = cur->next;
        }

        //考虑删除头节点的情况：即此时的倒数第n个节点，实际上就是第一个节点的时候，
        int rank = cnt - n;

        if (rank == 0) {
            cur = head;
            head = head->next;
            cur->next = nullptr;
            delete cur;
            return head;
        }

        cur = head;
        while ( -- rank)
        {
            cur = cur->next;
        }

        ListNode*tmp = cur->next;
        cur->next = tmp->next;
        tmp->next = nullptr;    //直接删除tmp指向的节点，实际上是没有删除tmp指针的，他可能会乱指
        delete tmp;

        return head;
    }
};

复杂度分析：

首先，该函数计算链表中的节点数，然后找到需要删除的节点，最后删除节点。

现在让我们来分析时间复杂度和空间复杂度：

时间复杂度：该函数包含两个主要步骤。第一个步骤是遍历整个链表以计算节点数，这步操作的时间复杂度是O(n)。第二个步骤是找到需要删除的节点并删除，最多需要再遍历n个节点，所以这步操作的时间复杂度也是O(n)。所以，总的时间复杂度是O(n + n) = O(2n)，但我们通常忽略常数，所以最终的时间复杂度是O(n)。

空间复杂度：该函数只使用了固定数量的额外空间，所以空间复杂度是O(1)。

总的来说，这个函数在时间和空间上都非常高效。

快慢指针：别人的

核心：双指针的经典应用，如果要删除倒数第n个节点，让fast移动n步，然后让fast和slow同时移动，直到fast指向链表末尾。删掉slow所指向的节点就可以了。
当你正序遍历的情况，想让一个指针指向倒数第n个值，那么就只需要让一个fast指针先走n步，然后slow指针最初在起点，这样的话，slow 和 fast指针就保持着n步的距离，最后slow必然可以指向倒数第n个节点！

这是有数学证明的，这里就不证明了！先记住！

而删除节点的话，最好找到删除节点的前一个节点，那么就让fast走先走n+1步即可！和slow拉开n+1步的距离，这样的话两个指针就拉开距离，使得slow只能走到倒数第n+1个节点！即倒数第n个节点的前一个节点！

实现代码：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        
        ListNode* dummyHead = new ListNode(0);
        dummyHead->next = head;
        ListNode* slow = dummyHead;
        ListNode* fast = dummyHead;
        n ++;
        
        while (n -- && fast != nullptr) {
            fast = fast->next;
        }

        while (fast != nullptr) {
            fast = fast->next;
            slow = slow->next;
        }

        ListNode* cur = slow->next;
        slow->next = cur->next;
        cur->next = nullptr;
        delete cur;

        return dummyHead->next;
    }
};

题目总结：

C++ 和 C需要手动管理内存，而java和python则不需要，是自动管理内存的！

面试题 02.07. 链表相交

题目链接：

解题思路：

别人的：

其实就是要知道如何找到相交节点的数学规律：
我们求出两个链表的长度，并求出两个链表长度的差值。
首先得定义两个指针，分别指向两个链表的头部，curA和curB吧，然后求出差值后，再让curA移动到curB末尾对齐的位置。
那么就可以开始判断了两个指针是否在交点处呢？

推荐
数学证明题解
有趣的题解

实现代码：

class Solution:
    def getIntersectionNode(self, headA: ListNode, headB: ListNode) -> ListNode:
        dis = self.getLength(headA) - self.getLength(headB)
        
        # 通过移动较长的链表，使两链表长度相等
        if dis > 0:
            headA = self.moveForward(headA, dis)
        else:
            headB = self.moveForward(headB, abs(dis))
        
        # 将两个头向前移动，直到它们相交
        while headA and headB:
            if headA == headB:
                return headA
            headA = headA.next
            headB = headB.next
        
        return None
    
    def getLength(self, head: ListNode) -> int:
        length = 0
        while head:
            length += 1
            head = head.next
        return length
    
    def moveForward(self, head: ListNode, steps: int) -> ListNode:
        while steps > 0:
            head = head.next
            steps -= 1
        return head

题目总结：

面试题掌握得不是太好！只弄明白了为什么会存在相遇，但是没有明白卡尔的做法为什么这么做。为什么A要从B的末尾开始！

142. 环形链表 II

题目链接

解题思路：

自己的：

首先我们看图：

L：从起点到环口的节点个数；
S1：从环口到相遇点的节点个数；
S2：从相遇点到环的起点的节点个数；

然后
之后补充吧！

实现代码：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        ListNode* slow, *fast;
        slow = fast = head;
        while (fast != NULL && fast->next != NULL)
        {
            fast = fast->next->next;
            slow = slow->next;

            if (slow == fast) {
                slow = head;
                while (slow != fast) {
                    slow = slow->next;
                    fast = fast->next;

                }
                return fast;
            }
        }
        return NULL;
    }
};

题目总结：

无！文章来源地址https://www.toymoban.com/news/detail-609413.html

到了这里，关于力扣[24、19、面试题02.07、142]的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！