中缀表达式转后缀表达式，使用逆波兰计算。可以计算小数-Toy模板网

这篇具有很好参考价值的文章主要介绍了中缀表达式转后缀表达式，使用逆波兰计算。可以计算小数。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

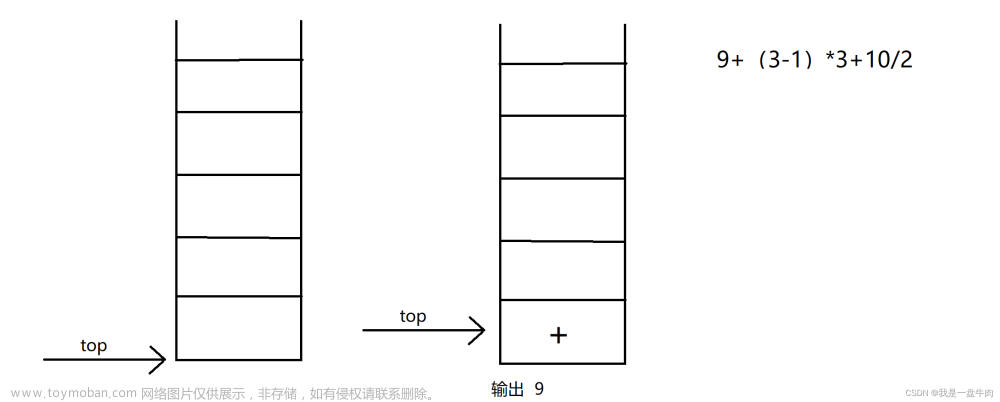
1、使用方法

传递一个分开保存符号与数字的List即可：List SumNumber;

获取参数的构造方法如下：

    public ReversePolish(List<String> sumNumber) {
        SumNumber = sumNumber;
    }

要求的List保存数据的方式如下：
例如：1+2+3
中缀表达式转后缀表达式，使用逆波兰计算。可以计算小数,数据结构,java,算法,数据结构
然后使用 EvaluatePostfixExpressions方法传递出一个保存好结果的String。文章来源地址https://www.toymoban.com/news/detail-609572.html

2、代码实现

package com.example.computermoblie;

import java.math.BigDecimal;
import java.math.RoundingMode;
import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.List;
import java.util.PriorityQueue;
import java.util.Queue;
import java.util.Stack;

public class ReversePolish {
    public List<String> SumNumber;


    Stack<BigDecimal> SymbolStack = new Stack<>();

    //表示没有计算错误的情况
    private boolean Error = false;

    public static final int LeftBrack = 0;   //左括号优先级
    public static final int AandS = 1;   //加减法
    public static final int MandD = 2;   //乘除
    public static final int RightBrack = 3;   //右括号优先级

    //中缀转后缀
    public Queue<String> InfixToSuffix() {
        Queue<String> queue = new ArrayDeque<>();
        Stack<String> swapStack = new Stack<>();

        for (int i = 0; i < SumNumber.size(); i++) {
            String isStr = SumNumber.get(i);

            if (!IsSymbol(isStr)) {
                queue.add(isStr); // 将数字直接添加到输出队列中
            } else {
                if (swapStack.isEmpty() || isStr.equals("(")) {
                    swapStack.push(isStr);
                } else if (isStr.equals(")")) {
                    if(!swapStack.isEmpty()){
                        while (!swapStack.peek().equals("(")) {
                            queue.add(swapStack.pop());
                        }
                        swapStack.pop(); // 弹出 "("
                    }
                } else {
                    while (!swapStack.isEmpty() && JudgmentPriority(swapStack.peek(), isStr)) {
                        queue.add(swapStack.pop());
                    }
                    swapStack.push(isStr);
                }
            }
        }

        while (!swapStack.isEmpty()) {
            queue.add(swapStack.pop());
        }

        return queue;
    }

    public String EvaluatePostfixExpressions() {
        Error = false;  // 表示运算未发现错误
        BigDecimal ret = null; // 表示最后的运算结果
        Queue<String> queue = InfixToSuffix();  // 获取后缀表达式

        Log.d("WQWQ",queue.toString());

        while (!queue.isEmpty()) {
            String str = queue.remove();

            if (!IsSymbol(str)) {
                //保存数据
                try {
                    BigDecimal number = new BigDecimal(str);
                    SymbolStack.push(number);
                } catch (NumberFormatException e) {
                    Log.d("Number","出现空值");
                }
            } else {
                if (SymbolStack.size() < 2) {
                    Error = true; // 栈中元素不足2个，运算错误
                    break;
                }

                BigDecimal op2 = SymbolStack.pop();
                BigDecimal op1 = SymbolStack.pop();
                BigDecimal result = null;

                switch (str) {
                    case "+":
                        result = op1.add(op2);
                        break;
                    case "-":
                        result = op1.subtract(op2);
                        break;
                    case "×":
                        result = op1.multiply(op2);
                        break;
                    case "÷":
                        if (op2.compareTo(BigDecimal.ZERO) == 0) {
                            Error = true; // 除数为零，运算错误
                            break;
                        }
                        result = op1.divide(op2, 3, RoundingMode.HALF_UP);
                        break;
                    default:
                        Error = true; // 非法的运算符，运算错误
                        break;
                }

                if (Error) {
                    break;
                } else {
                    SymbolStack.push(result);
                }
            }
        }

        if (Error) {
            return "Error"; // 出现错误后直接返回错误信息
        } else {
            if (!SymbolStack.isEmpty()) {
                ret = SymbolStack.pop();
            }
            // 使用toEngineeringString()方法将结果输出为工程计数法
            return ret.toEngineeringString();
        }
    }

    public ReversePolish(List<String> sumNumber) {
        SumNumber = sumNumber;
    }

    //判断是否为符号
    public boolean IsSymbol(String str) {
        boolean isSymbole = false;
        if (str.equals("+")) {
            isSymbole = true;
        } else if (str.equals("-")) {
            isSymbole = true;
        } else if (str.equals("×")) {
            isSymbole = true;
        } else if (str.equals("÷")) {
            isSymbole = true;
        } else if (str.equals("(")) {
            isSymbole = true;
        } else if (str.equals(")")) {
            isSymbole = true;
        }

        return isSymbole;
    }

    //判断优先级
    public boolean JudgmentPriority(String PreantStr, String SunStr) {
        //默认PreantStr优先级小于SunStr
        boolean value = false;

        if (SymbolValue(PreantStr) >= SymbolValue(SunStr)) {
            value = true;
        }

        return value;
    }

    //判断属于什么符号
    public int SymbolValue(String str) {
        int Value = LeftBrack;

        if (str.equals("+")) {
            Value = AandS;
        } else if (str.equals("-")) {
            Value = AandS;
        } else if (str.equals("×")) {
            Value = MandD;
        } else if (str.equals("÷")) {
            Value = MandD;
        } else if (str.equals("(")) {
            Value = LeftBrack;
        } else if (str.equals(")")) {
            Value = RightBrack;
        }
        return Value;
    }

    public List<String> getSumNumber() {
        return SumNumber;
    }
}