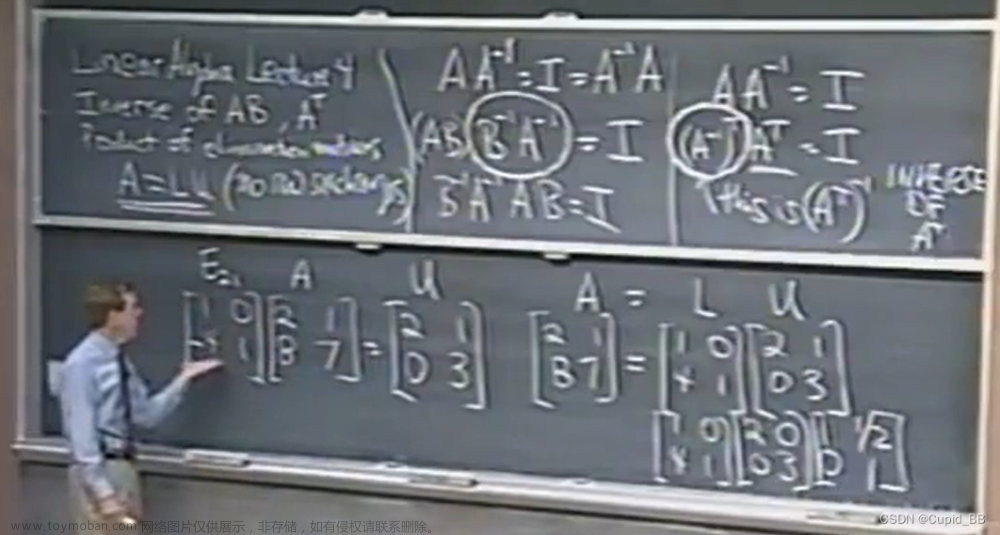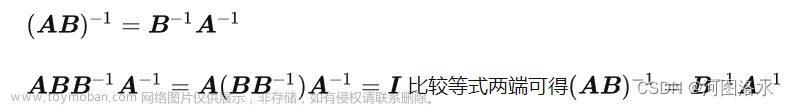2022.10.15 ~ 2022.11.
立个flag，每天一到两刷。
第一章 方程组的几何解释
行图像和列图像（2 x 2的例子）：
行图像：
对于行图像，n=2，即两方程两未知数，两条直线的交点就是方程的解。
列图像
该方程的目的是什么？
目的是寻找正确的线性组合。上图红框部分就是列向量的线性组合。
x=1，y=2的线性组合可以得出b。而所有的线性组合可以求出所有可能的右侧向量。
行图像和列图像（3 x3 的例子）：
行图像
解第二个方程得到三个点，这三个点组成一个平面。
所有满足方程的点组成平面。对于线性方程，所有解的图像就是一个平面。
所以，3 x 3问题的每一行都是三维空间的一个平面。两个平面相交于一条直线，因此三维空间中的两个方程确定一条直线。三个平面相交于一点。
对于三维问题，行图像由三个平面构成，只要计算正确，三个平面必然相交于一点，这就是解。
列图像
现在问题是：根据上图的方程，将三个向量进行组合，求得右侧向量。
现在考虑，不管b是多少，是否都能求解方程？这等价于，对于任意b，是否能求解Ax=b？用“线性组合”的语言来问这个问题，就是说列的向量组合是否能覆盖整个三维空间？（任意b，也就是三维空间的任意点）
答案是不能。举个例子，在三维空间中，如果三个列向量都在同一平面，那么其组合也在该平面上，这时候不管怎么组合，都得不出它们平面以为的向量。这个时候若b出现在平面外，则没有解。也就是说当组合不在同一平面内时，才能覆盖整个三维空间。
线性相关＝同一平面＝满秩＝行列式不等于0。
当你有多个向量，并且可以移除其中一个而不减小张成的空间，当这种情况发生时，我们称它们是“线性相关”的。
另一方面，如果所有向量都给张成的空间增添了新的维度，它们被称为“线性无关”的。
矩阵乘向量
第一种方法，一次取一列。（视频作者表示更喜欢这种）
取1个第一列，2个第二列，然后相加。也就是看作A各列的线性组合。
在对比前面的方程组(下图)，就豁然开朗了。Ax=b，x矩阵就是A各列的线性组合的解。
第二种方法，一次取一行。
这个方法就是我们国内经典的矩阵乘法，就不列举了。
第一章总结
矩阵可以分为行矩阵和列矩阵形式：
行矩阵看的话
- 两个变量就是二维空间，也就是线，两线成一点。
- 三个变量就是三维空间，也就是面，三面成一点。
列矩阵看的话
- 两个变量是两个向量的和。
- 三个变量是三个向量的和。
列矩阵形式更符合我们的式子Ax＝b，更方便看和理解，但是行矩阵是国内通用写法。
对于三维空间，如果有一个变量是没有用或者与前面重叠，那么三维被压为二维，这个时候我们求出的就是线，而非点（两面交一线）。因此不是所有b都是可以求出的。
第二章 矩阵消元
矩阵A首先通过消元得到上三角矩阵，记为U。
2.1 消元失效
那么，其实也是存在消元失效的例子的，什么是消元失败呢？
上面的例子，消元失效指的是不能得到三个主元。那么假设上面A矩阵第一行变成[0,2,1]，即方程一中没有x。这意味着就无解了嘛？
不是的，我们只需要进行行交换即可。所以如果0占据了主元的位置，这时就需要交换行。
行交换可以解决主元为0的“暂时性失效”，但当底下的行中再也没有非0元素时，消元就彻底失效了。
把方程组和解也加到矩阵里面称为“增广矩阵”。
那么我们通过增广矩阵得到了矩阵U和矩阵C，接着把结果写成方程：
2.2 回代
那么怎么求解上面那个U和C得到的方程呢？先从第三个方程得到z，再通过z和第二个方程得到y，以此类推。这就是回代。
什么是“回代”？
它是反向求解方程的简单步骤。因为方程组是三角的，所以反向。
24:10
2.3 行变换和列变换
【矩阵乘向量】看作是“矩阵列的线性组合”
【向量乘矩阵】看作是“矩阵行的线性组合”
在左边用矩阵做乘法，进行的是行变换。
在右边用矩阵做乘法，进行的是列变换。
文章来源：https://www.toymoban.com/news/detail-609607.html
这里就是一次取一列，取这一列乘0 = 0，取这一列乘1 = 。所以结果矩阵的第一列为 文章来源地址https://www.toymoban.com/news/detail-609607.html
到了这里，关于MIT线性代数详细笔记（更新中）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
