1. Toy模板网首页
  2. > Toy博客

C数据结构与算法——队列 应用（C语言纯享版 迷宫）

7月前 作者：小丶象 分类：Toy博客 阅读(31) 违法举报

这篇具有很好参考价值的文章主要介绍了C数据结构与算法——队列 应用（C语言纯享版 迷宫）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

实验任务

(1) 掌握顺序循环队列及其C语言的表示；
(2) 掌握入队、出队等基本算法的实现；
(3) 掌握顺序循环队列的基本应用（求解迷宫通路）。

实验内容

  • 使用C语言实现顺序循环队列的类型定义与算法函数；
  • 编写main()函数并根据需要修改、补充相关的类型定义与函数，以实现“求解迷宫通路”问题：
  • 求解迷宫通路问题描述：
    • 给定一个M×N的迷宫图，指定一个入口与一个出口；
    • 规定行走规则为：按“上右下左”优先顺序向相邻空位移动1格，用（i，j）表示迷宫中的第i行第j列的一个方块
    • 在迷宫外围加上围墙；
  • 实现指定入口和出口的固定迷宫；
  • 实现随机入口和出口的固定迷宫；
  • 实现障碍、入口和出口都随机的迷宫。

实验源码

注意：必须在Dos窗口下运行，并且以管理员身份打开Dos窗口最佳

#include <stdio.h>
#include <time.h>
#include "windows.h"

#define MAXSIZE 1000
#define ROW 15
#define LINE 15
#define RATIO 0.6875 // 44/64的比例
#define COORDINATE -1 // 坐标默认 值
#define DISTOP 5 // 迷宫距离顶端距离格数

#define PASS 0 // 通路
#define WALL 1 // 墙
#define ENTRY 2 // 入口
#define EXIT 3 // 出口
#define DEAD 5 // 死路

// 延时设置
int walkDelay = 500;
int dirDelay = 1000;

typedef struct Box {
    int x;           // 点的横坐标（行）
    int y;           // 点的纵坐标（列）
    int pre;         // 上一个点的下标
} Box;

typedef struct {
    Box *base;
    int front;
    int rear;
} SqQueue;

void Map(int map[][LINE]); // 生成地图

void KnuthShuffle(int map[], int length); // 洗牌算法

void swapInt(int *a, int *b); // 辅助洗牌算法 交换

void PrintMap(int map[][LINE]); // 打印迷宫地图

boolean InitQueue(SqQueue *queue); // 循环队列的初始化

void Walk(SqQueue *queue, int in_x, int in_y, int map[][LINE]); // 移动迷宫

boolean EnQueue(SqQueue *queue, Box node); // 循环队列入队列

boolean IsFull(SqQueue *queue); // 判队满

boolean IsEmpty(SqQueue *queue); // 判队空

Box DeQueue(SqQueue *queue); // 循环队列出队列

void ShowPath(SqQueue *queue, int end); // 求解最短路径

void Color(short x); // 自定义函根据参数改变颜色

void DirTest(int map[][LINE], int dir, int j, int k); // 方向试探

void DeadPath(int j, int k); // 置为死路

void GotoXY(int x, int y); // 将光标移至屏幕 第x列，第y行 处

void DisplayQueue(SqQueue *queue); // 队列动态展示

void HideCursor(void); // 隐藏光标

/**
 * <h2>顺序队列实验</h2>
 * <h3>随机迷宫问题</h3>
 * <h3>注意：请在Dos窗口下运行</h3>
 * <h4>非循环队列，并不是真的退出队列</h4>
 * @return 0
 */
int main() {

    GotoXY(0, 0);
    Color(9);
    printf("  使用队列解决迷宫通路问题 \n");
    GotoXY(0, 1);
    printf("==============================\n");
    GotoXY(0, 2);
    Color(12);
    printf("Ｘ--走过的无效通路");
    Color(9);
    printf("  囚--起点\n");
    GotoXY(0, 3);
    Color(13);
    printf("Ｏ--走过的有效通路");
    Color(11);
    printf("  口--终点\n");
    GotoXY(0, 4);
    printf("------------------------------\n");

    srand(time(NULL));

    int map[ROW][LINE];
    Map(map);
    PrintMap(map);

    SqQueue queue;
    if (!(InitQueue(&queue))) {
        printf("队列初始化失败~~\n");
        return 0;
    }

    int in_x, in_y;
    for (int i = 0; i < ROW; i++) {
        for (int j = 0; j < LINE; j++) {
            if (map[i][j] == ENTRY) {
                in_x = i;
                in_y = j;
            }
        }
    }

    HideCursor();
    DisplayQueue(&queue);
    Walk(&queue, in_x, in_y, map);

    getchar();
}

void Map(int map[][LINE]) {
    int length = (ROW - 2) * (LINE - 2); // 8 * 8 内区域
    int randArr[length];
    for (int i = 0; i < length; i++) {
        if (i == 0) {
            randArr[i++] = ENTRY;
            randArr[i++] = EXIT;
        }
        if (i < (length * RATIO) + 2) {
            randArr[i] = PASS;
        } else {
            randArr[i] = WALL;
        }
    }
    KnuthShuffle(randArr, length); // 打乱 内区域
    // 赋值整张地图
    for (int i = 0; i < ROW; i++) {
        for (int j = 0; j < LINE; j++) {
            // 这里一个小技巧：只要前面四个表达式一个为假，说明未到边界赋值，保证Length不会越界
            if (i != 0 && i != ROW - 1 && j != 0 && j != LINE - 1 && length--) {
                map[i][j] = randArr[length];
            } else {
                map[i][j] = WALL;
            }
        }
    }
}

void KnuthShuffle(int map[], int length) {
    for (int i = length - 1; i >= 1; i--) {
        swapInt(&map[i], &map[rand() % (i + 1)]);
    }
}

void swapInt(int *a, int *b) {
    int t;
    t = *a;
    *a = *b;
    *b = t;
}

void PrintMap(int map[][LINE]) {
    for (int i = 0; i < ROW; i++) {
        for (int j = 0; j < LINE; j++) {
            GotoXY(j * 2, i + DISTOP);
            switch (map[i][j]) {
                case PASS:
                    printf("　");
                    break;
                case WALL:
                    Color(10);
                    printf("围");
                    break;
                case ENTRY:
                    Color(9);
                    printf("囚");
                    break;
                case EXIT:
                    Color(11);
                    printf("口");
                    break;
            }
        }
        printf("\n");
    }
    Sleep(3000);
}

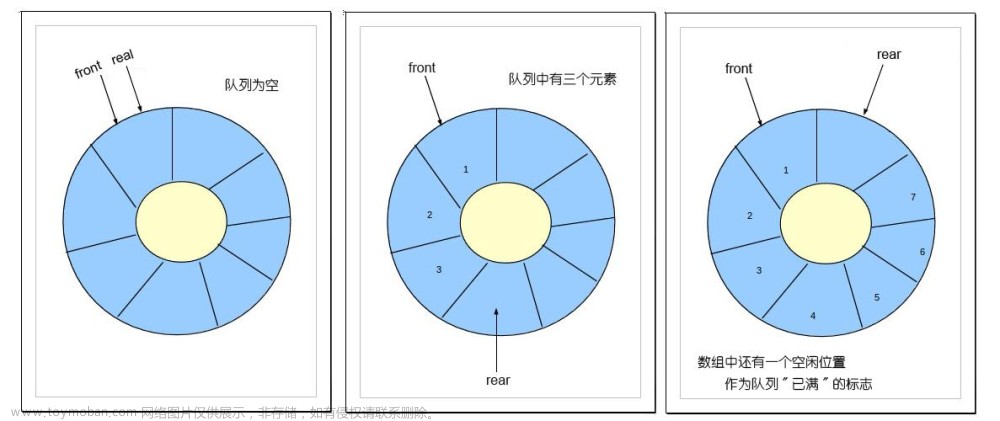
boolean InitQueue(SqQueue *queue) {
    queue->base = (Box *) malloc(sizeof(Box) * MAXSIZE);
    if (!(queue->base)) {
        return FALSE;
    }
    queue->front = queue->rear = 0;
    return TRUE;
}

void Walk(SqQueue *queue, int in_x, int in_y, int map[][LINE]) {
    // 起点先入队列
    Box node; // 生成当前位置(起点)
    node.x = in_x;
    node.y = in_y;
    node.pre = COORDINATE; // 起点位置下标 -1

    EnQueue(queue, node); // 起点入队列

    while (!(IsEmpty(queue))) { // 无路可走的情况，回到起点
        node = DeQueue(queue); // 取出队头位置 队头指针front++

        if (map[node.x][node.y] == EXIT) { // 判断当前位置是否是终点
            ShowPath(queue, queue->front);
            return;
        }
        int dir; // 装方向
        Box tNode; // 生成下一个位置
        for (dir = 0; dir < 4; dir++) { // 判断当前位置各个方向是否可走
            switch (dir) {
                case 0:
                    tNode.x = node.x - 1;
                    tNode.y = node.y;
                    DirTest(map, dir, node.x, node.y);
                    break;
                case 1:
                    tNode.x = node.x;
                    tNode.y = node.y + 1;
                    DirTest(map, dir, node.x, node.y);
                    break;
                case 2:
                    tNode.x = node.x + 1;
                    tNode.y = node.y;
                    DirTest(map, dir, node.x, node.y);
                    break;
                case 3:
                    tNode.x = node.x;
                    tNode.y = node.y - 1;
                    DirTest(map, dir, node.x, node.y);
                    break;
            }
            if (map[tNode.x][tNode.y] == PASS || map[tNode.x][tNode.y] == EXIT) { // 判断这个方向 是否可走
                tNode.pre = queue->front - 1; // 把节点位置的下标给 新位置
                EnQueue(queue, tNode); // 入队
                if (map[tNode.x][tNode.y] == PASS) {
                    map[tNode.x][tNode.y] = DEAD;
                    DeadPath(tNode.x, tNode.y);

                }
            }
        }
    }
    // 这里加二号条件的原因是：此程序使用的是终点出队列即停止，但是也不排除 到终点即为空
    if (IsEmpty(queue) && map[node.x][node.y] != EXIT) {
        GotoXY(0, ROW + DISTOP + 2);
        Color(12);
        printf("\t无路可走，死翘翘了~~\n");
    }
}

boolean EnQueue(SqQueue *queue, Box node) {
    if (IsFull(queue)) {
        return FALSE;
    }
    queue->base[queue->rear] = node; // 新元素插入队尾
    queue->rear = queue->rear + 1; // 队尾指针加 1
    DisplayQueue(queue);
    return TRUE;
}

boolean IsFull(SqQueue *queue) {
    return queue->rear + 1 == queue->front; // 非循环队列
}

boolean IsEmpty(SqQueue *queue) {
    return queue->rear == queue->front;
}

Box DeQueue(SqQueue *queue) {
    Box box = queue->base[queue->front++];
    DisplayQueue(queue);
    return box; // 取出队头元素，并把其出队列
}

void ShowPath(SqQueue *queue, int end) {
    int i, tmp;
    for (i = end - 1; i >= 0;) {
        tmp = queue->base[i].pre;
        queue->base[i].pre = COORDINATE;
        i = tmp;
    }
    int count = 0, ti;
    for (i = 1; i < end; i++) { // i = 1, 保证不是终点即可
        if (queue->base[i].pre == COORDINATE) {
            if (count == 0) {
                GotoXY(LINE * 2 + 35, DISTOP - 1);
                printf("↓ 路径打印 ↓");
                GotoXY(LINE * 2 + 35, DISTOP);
                printf("|__i__j__pre__|");
            }
            count++;
            GotoXY(LINE * 2 + 35, DISTOP + count);
            printf("|_____________|\n");
            Color(11);
            GotoXY(LINE * 2 + 35 + 3, DISTOP + count);
            printf("%d", queue->base[i].x);
            GotoXY(LINE * 2 + 35 + 7, DISTOP + count);
            printf("%d", queue->base[i].y);
            GotoXY(LINE * 2 + 35 + 10, DISTOP + count);
            printf("%d", queue->base[i].pre);
            if (count == 1) {
                ti = i;
                continue;
            }
            GotoXY(queue->base[ti].y * 2, queue->base[ti].x + DISTOP);
            Color(15);
            if (queue->base[i].x - queue->base[ti].x == -1 &&
                queue->base[i].y - queue->base[ti].y == 0) {
                printf("↑");
            } else if (queue->base[i].x - queue->base[ti].x == 0 &&
                       queue->base[i].y - queue->base[ti].y == 1) {
                printf("→");
            } else if (queue->base[i].x - queue->base[ti].x == 1 &&
                       queue->base[i].y - queue->base[ti].y == 0) {
                printf("↓");
            } else {
                printf("←");
            }
            ti = i;
        }
    }
}

void Color(short x) {
    if (x >= 0 && x <= 15) { // 参数在0-15的范围颜色
        SetConsoleTextAttribute( // 调用设置控制台文本属性函数(调用获取句柄函数(不理解), 不理解)
                GetStdHandle(STD_OUTPUT_HANDLE), x);    // 只有一个参数，改变字体颜色
    } else { // 默认的颜色白色
        SetConsoleTextAttribute(GetStdHandle(STD_OUTPUT_HANDLE), 7);
    }
}

void DirTest(int map[][LINE], int dir, int j, int k) {
    GotoXY(k * 2, j + DISTOP);
    Color(15);
    switch (dir) {
        case 0:
            printf("↑");
            break;
        case 1:
            printf("→");
            break;
        case 2:
            printf("↓");
            break;
        case 3:
            printf("←");
            break;
    }
    Sleep(dirDelay);
    GotoXY(k * 2, j + DISTOP);
    Color(13);
    switch (map[j][k]) {
        case ENTRY:
            Color(9);
            printf("囚");
            break;
        case DEAD:
            Color(12);
            printf("Ｘ");
            break;
    }
}

void DeadPath(int j, int k) {
    GotoXY(k * 2, j + DISTOP);
    Color(12);
    printf("Ｘ");
    Sleep(walkDelay);
}

void GotoXY(int x, int y) {
    COORD pos = {x, y}; // 坐标
    HANDLE hOut = GetStdHandle(STD_OUTPUT_HANDLE); // 获取句柄（标准输出句柄）
    SetConsoleCursorPosition(hOut, pos); // 设置控制台光标位置
}

void DisplayQueue(SqQueue *queue) {
    int len = ROW - 1;
    Color(12);
    GotoXY(LINE * 2 + 10, DISTOP);
    printf("|__i__j__di__| <- top");
    for (int j = 1; j <= len; j++) {
        GotoXY(LINE * 2 + 10, DISTOP + j);
        printf("|____________|\n");
    }
    int length = queue->rear;
    for (int i = 0; i < length; i++, len--) {
        if (len == 0) {
            len = ROW - 1;
            for (int j = 1; j <= len; j++) {
                GotoXY(LINE * 2 + 10, DISTOP + j);
                printf("|____________|\n");
            }
        }
        Color(11);
        GotoXY(LINE * 2 + 10 + 3, DISTOP + len);
        printf("%d", queue->base[i].x);
        GotoXY(LINE * 2 + 10 + 7, DISTOP + len);
        printf("%d", queue->base[i].y);
        GotoXY(LINE * 2 + 10 + 10, DISTOP + len);
        printf("%d", queue->base[i].pre);
    }
}

void HideCursor(void) {
    CONSOLE_CURSOR_INFO cursor_info = {1, 0};
    SetConsoleCursorInfo(GetStdHandle(STD_OUTPUT_HANDLE), &cursor_info);
}

实验结果

C数据结构与算法——队列 应用（C语言纯享版 迷宫）,C,c语言,开发语言,学习,经验分享,算法,数据结构文章来源地址https://www.toymoban.com/news/detail-609734.html

到了这里，关于C数据结构与算法——队列 应用（C语言纯享版 迷宫）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处： 如若内容造成侵权/违法违规/事实不符，请点击违法举报进行投诉反馈，一经查实，立即删除！

分享到：
领支付宝红包 赞助服务器费用

相关文章

  • 【脚踢数据结构】图（纯享版）

    【脚踢数据结构】图（纯享版）

    (꒪ꇴ꒪ )，Hello我是 祐言QAQ 我的博客主页：C/C++语言，Linux基础，ARM开发板，软件配置等领域博主🌍 快上🚘，一起学习，让我们成为一个强大的攻城狮！ 送给自己和读者的一句鸡汤🤔： 集中起来的意志可以击穿顽石! 作者水平很有限，如果发现错误，可在评论区指正，感谢

    2024年02月12日
    浏览(21)
  • 【数据结构与算法分析】使用C语言实现队列的两种（带头结点与不带头结点）链式存储，并且给出一种循环队列的设计思想

    【数据结构与算法分析】使用C语言实现队列的两种（带头结点与不带头结点）链式存储，并且给出一种循环队列的设计思想

      当我们编写程序时，经常需要处理各种数据结构。队列是一种常见的数据结构，它有着广泛的应用场景。队列的基本操作包括入队和出队，应用于模拟等待队列、消息队列、计算机缓存等场合。   在实际编程中，我们可以用不同的数据结构来实现队列。本文主要介绍了

    2024年02月08日
    浏览(43)
  • 《数据结构、算法与应用C++语言描述》-列车车厢重排问题

    《数据结构、算法与应用C++语言描述》-列车车厢重排问题

    完整可编译运行代码见：Github::Data-Structures-Algorithms-and-Applications/_10Train_carriages_rearrangement/ 一列货运列车有 n 节车厢，每节车厢要停靠在不同的车站。假设 n个车站从 1 到n 编号，而且货运列车按照从n到1的顺序经过车站。车厢的编号与它们要停靠的车站编号相同。为了便于从

    2024年04月10日
    浏览(45)
  • 【数据结构和算法】--队列的特殊结构-循环队列

    【数据结构和算法】--队列的特殊结构-循环队列

    循环队列是队列的一种特殊结构，它的 长度是固定的 k ，同样是 先进先出 ，理论结构是 首尾相连的环形循环结构 。其理论结构大致如下： 具体结构描述可以参考 LeetCode : 622. 设计循环队列的题目要求，大致如下： 设计你的循环队列实现。 循环队列是一种 线性数据结构 ，

    2024年02月04日
    浏览(35)
  • 数据结构——队列（C语言）

    数据结构——队列（C语言）

    本篇文章将解决一下几个问题： 队列是什么？ 如何实现一个队列？ 什么场景下会用队列？ 队列：一种只允许一端进行插入数据操作，在另一端进行删除操作的特殊线性表。队列具有先进先出（FIFO）入队列：进行插入操作的一端称为队尾，出队列的一端叫做队头。  队列也

    2024年02月11日
    浏览(27)
  • 数据结构学习记录——图应用实例-拯救007（问题描述、解题思路、伪代码解读、C语言算法实现）

    数据结构学习记录——图应用实例-拯救007（问题描述、解题思路、伪代码解读、C语言算法实现）

    目录 问题描述  解题思路 伪代码  总体算法 DFS算法 伪代码解读 总体算法 DFS算法 具体实现（C语言） 在老电影“007之生死关头”（Live and Let Die）中有一个情节，007被毒贩抓到一个鳄鱼池中心的小岛上，他用了一种极为大胆的方法逃脱 —— 直接踩着池子里一系列鳄鱼的大脑

    2024年02月05日
    浏览(50)
  • 【头歌】数据结构-队列的应用

    【头歌】数据结构-队列的应用

      第1关：循环队列 任务描述 本关任务：编写一个循环队列，实现入队、出队操作，判断队空、队满等特殊情况。 相关知识 为了完成本关任务，你需要掌握：1.循环队列定义，2.入队、出队的定义，3.队空、队满的情况。 循环队列定义 循环队列将数组存储区看成是一个首尾相

    2024年02月08日
    浏览(31)
  • 【数据结构和算法】--队列

    【数据结构和算法】--队列

    队列是只允许在一端进行插入数据操作，在另一端进行删除数据操作的特殊线性表，队列具有 先进先出 FIFO(First In First Out) 的原则。 入队列 ：进行 插入操作的一端称为队尾 。 出队列 ：进行 删除操作的一端称为队头 。 队列结构联想起来也非常简单，如其名，队列就相当于

    2024年02月05日
    浏览(32)
  • 队列——“数据结构与算法”

    队列——“数据结构与算法”

    各位CSDN的uu们你们好呀，又好久不见啦，最近有点摆烂，甚是惭愧！！！！今天，小雅兰的内容是队列，下面，让我们进入队列的世界吧！！！ 队列 队列的概念及结构 队列：只允许在一端进行插入数据操作，在另一端进行删除数据操作的特殊线性表，队列具有先进先出FIF

    2024年02月06日
    浏览(31)
  • 算法与数据结构-队列

    算法与数据结构-队列

      队列跟栈一样，也是一种操作受限的线性表数据结构。不过，队列是先进者先出。   栈只支持两个基本操作：入栈 push()和出栈 pop()。队列跟栈非常相似，支持的操作也很有限，最基本的操作也是两个：入队 enqueue()，放一个数据到队列尾部；出队 dequeue()，从队列头部取

    2024年02月12日
    浏览(32)

觉得文章有用就打赏一下文章作者

支付宝扫一扫打赏

博客赞助

微信扫一扫打赏

请作者喝杯咖啡吧~博客赞助

支付宝扫一扫领取红包，优惠每天领

二维码1

领取红包

二维码2

领红包