1. Toy模板网首页
  2. > Toy博客

最优化方法

9月前 作者：温九味闻醉 分类：Toy博客 阅读(36) 违法举报

这篇具有很好参考价值的文章主要介绍了最优化方法。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

一. 图论

1.最小生成树

图的生成树是它的一颗含有其所有顶点的无环连通子图,一 幅加权图的最小生成树(MST)是它的一颗权值(树中的所有边的权值之和) 最小的生成树
• 适用场景：道路规划、通讯网络规划、管道铺设、电线布设等

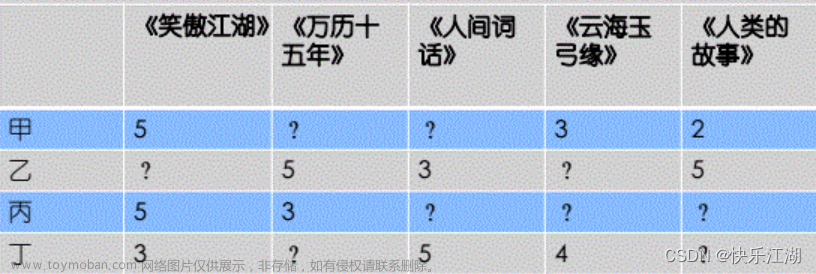
题目数据
kruskal算法
稀疏图，按边大小排序

#include<bits/stdc++.h>
using namespace std;
const int maxn=5e3+3,maxm=2e5+5;

int n,m;
struct node{
    int fr,to,val;
    inline bool operator<(node b)const {
        return val<b.val;
    }
}e[maxm<<1];
int k,fa[maxn];
inline void add(int x,int y,int z){e[++k]=(node){x,y,z};}

inline int find(int x){
    return fa[x]==x?x:fa[x]=find(fa[x]);
}
int main()
{
    scanf("%d %d",&n,&m);
    int x,y,z;
    for(int i=1;i<=m;i++) 
    {
      	scanf("%d %d %d",&x,&y,&z);
        add(x,y,z);
        add(x,y,z);//无向图 
    }
    sort(e+1,e+k+1); //边排序
    
    for(int i=1;i<=n;i++)fa[i]=i;//并查集初始化
    int cnt=0,ans=0;
    for(int i=1;i<=k;i++)
    {
        int x=find(e[i].fr),y=find(e[i].to);
        if(x!=y)
        {
            fa[x]=y;//连边
            ans+=e[i].val;
            ++cnt;
            if(cnt==n-1)break;
        }
    }
    if(cnt==n-1)printf("%d",ans);
    else puts("orz");//图不连通
    return 0;
}

prim
稠密图

#include<bits/stdc++.h>
#define re return
#define inc(i,l,r) for(int i=l;i<=r;++i)
using namespace std;

const int maxn=5e3+3,maxm=2e5+5;
int inf=5e8;
int n,m,d[maxn][maxn],dis[maxn],vis[maxn];
int main()
{
   // freopen("a.in","r",stdin);
   	scanf("%d %d",&n,&m);
    int x,y,z;
    inc(i,1,n)inc(j,1,n)d[i][j]=inf;
    inc(i,1,m)
    {
        scanf("%d %d %d",&x,&y,&z);
        d[x][y]=d[y][x]=min(d[x][y],z);
    }
    
    vis[1]=1;//将1号点加入图中 
    inc(i,2,n)dis[i]=d[1][i];//dis初始化为1到各个点之间的最短距离 
    
    int ans=0,cnt=n-1;
    while(cnt--)//需要进行n-1次循环 
    {
        int now,minn=inf;
        inc(i,1,n)
        if(!vis[i]&&dis[i]<minn)minn=dis[i],now=i;//找当前最短距离点 now
        
     
        if(minn==inf)
        {
        	printf("orz");
        	re 0;
		}   
		vis[now]=1;
        ans+=dis[now];
        
        inc(i,1,n)dis[i]=min(dis[i],d[now][i]);
    }
    printf("%d",ans);
    re 0;
}

2.网络流

通常可以把这些边想象成道路，流量就是这条道 路的车流量，容量就是道路可承受的最大的车流量 • 适用场景：企业生产运输问题、交通拥堵优化问题等

最大流
题目数据

#include<bits/stdc++.h>
#define re return
#define inc(i,l,r) for(int i=l;i<=r;++i)
using namespace std;
template<typename T>inline void rd(T&x)
{
	char c;bool f=0;
	while((c=getchar())<'0'||c>'9')if(c=='-')f=1;
	x=c^48;
	while((c=getchar())>='0'&&c<='9')x=x*10+(c^48);
	if(f)x=-x;
}
const int maxn=1e4+4,maxm=1e5+5; 
int n,m,hd[maxn],s,t;
struct node{
	int to,nt,w;
}e[maxm<<1];
int k=1;
inline void add(int x,int y,int z)
{
	e[++k]=(node){y,hd[x],z};hd[x]=k;
	e[++k]=(node){x,hd[y],0};hd[y]=k;
}

int deep[maxn],cur[maxn];
inline bool bfs()
{
	inc(i,1,n)deep[i]=0;
	deep[s]=1;
	queue<int>q;
	q.push(s);
	while(!q.empty())
	{
		int x=q.front();
		q.pop();
		for(int i=hd[x];i;i=e[i].nt)
		{
			int v=e[i].to;
			if(!deep[v]&&e[i].w)
			{
				deep[v]=deep[x]+1;
				if(v==t)re 1;
				q.push(v);
			}
		}
	}
	re 0;
}

inline int dfs(int x,int flow)
{
	if(x==t)re flow;
	int delta=flow;
	for(int &i=cur[x];i;i=e[i].nt)
	{
		int v=e[i].to;
		if(deep[v]==deep[x]+1&&e[i].w)
		{
			int d=dfs(v,min(e[i].w,delta));
			e[i].w-=d;e[i^1].w+=d;
			delta-=d;
			if(!delta)re flow;
		}
	}
	re flow-delta;
}
int main()
{
	rd(n),rd(m),rd(s),rd(t);
	int x,y,w;
	inc(i,1,m)
	{
		rd(x),rd(y),rd(w);
		add(x,y,w);
	}
	
	int ans=0;
	while(bfs())
	{
		inc(i,1,n)cur[i]=hd[i];
		ans+=dfs(s,2147483647);
	}
	printf("%d",ans);
	re 0;
}

最小费用最大流
最大流量的基础上要求最小的费用，有边权值
题目数据

#include<bits/stdc++.h>
#define re return
#define inc(i,l,r) for(int i=l;i<=r;++i)
using namespace std;
template<typename T>inline void rd(T&x)
{
	char c;bool f=0;
	while((c=getchar())<'0'||c>'9')if(c=='-')f=1;
	x=c^48;
	while((c=getchar())>='0'&&c<='9')x=x*10+(c^48);
	if(f)x=-x;
}
const int maxn=5e3+3;

int k=1,n,m,s,t;
int dis[maxn],ord[maxn],hd[maxn],flow[maxn],vis[maxn];
int smoney,sflow;

struct node{
	int flow,to,nt,cost;
}e[100005];
inline void add(int u,int v,int w,int f)
{
	e[++k].to=v;e[k].nt=hd[u];e[k].flow=w;e[k].cost=f;hd[u]=k;
}

inline bool spfa()
{
	queue<int>q;
	memset(dis,0x3f3f3f3f,sizeof dis);
	memset(vis,0,sizeof vis);
	q.push(s);
	dis[s]=0;
	flow[s]=0x3f3f3f3f;
	while(!q.empty())
	{
		int x=q.front();
		q.pop();
		vis[x]=0;
		for(int i=hd[x];i;i=e[i].nt)
		{
			int v=e[i].to,w=e[i].flow,f=e[i].cost;
			if(w&&dis[v]>dis[x]+f)
			{
				if(!vis[v])
				{
					vis[v]=1;
					q.push(v);
				}
				flow[v]=min(flow[x],w);
				dis[v]=dis[x]+f;
				ord[v]=i;
			}
		}
	}
	re dis[t]!=0x3f3f3f3f;
}

inline void vivi()
{
	int x=t;
	while(x!=s)
	{
		int i=ord[x];
		e[i].flow-=flow[t];
		e[i^1].flow+=flow[t];
		x=e[i^1].to;
	}
	sflow+=flow[t];
	smoney+=flow[t]*dis[t];
}
int main()
{
//	freopen("a.in","r",stdin);
	rd(n),rd(m),rd(s),rd(t);
	int u,v,w,f;
	inc(i,1,m)
	{
		rd(u),rd(v),rd(w),rd(f);
		add(u,v,w,f);
		add(v,u,0,-f);
	}
	while(spfa())
		vivi();
	printf("%d %d",sflow,smoney);
	re 0;
}

3.最短路

主要包括Dijkstra算法和Floyd算法两种，用于求解 两点间的最短距离 • 适用场景：路径规划问题，如修建道路、设定救援路线等
题目数据
最优化方法,数学建模,图论,算法,深度优先

spfa

单源最短路
容易被卡

#include<bits/stdc++.h>
#define re return
#define inc(i,l,r) for(int i=l;i<=r;++i)
using namespace std;
template<typename T>inline void rd(T&x)
{
    char c;bool f=0;
    while((c=getchar())<'0'||c>'9')if(c=='-')f=1;
    x=c^48;
    while((c=getchar())>='0'&&c<='9')x=x*10+(c^48);
    if(f)x=-x;
}

const int maxn=1e4+5,maxm=5e5+5;
int n,m,hd[maxn];
struct node{
    int to,nt,val;
}e[maxm<<1];
int k,s;
inline void add(int x,int y,int z){
    e[++k]=(node){y,hd[x],z};hd[x]=k;
}

#define ll long long
ll inf=2147483647,dis[maxn],vis[maxn];
inline void spfa()
{
    inc(i,1,n)dis[i]=inf;
    dis[s]=0;
    queue<int>q;
    q.push(s);
    while(!q.empty())
    {
        int x=q.front();
        q.pop();
        vis[x]=0;
        for(int i=hd[x];i;i=e[i].nt)
        {
            int v=e[i].to;
            if(dis[v]>dis[x]+e[i].val)
            {
                dis[v]=dis[x]+e[i].val;
                if(!vis[v])
                {
                    vis[v]=1;
                        q.push(v);    
                }
            }
        }
    }
}

int main()
{
   // freopen("a.in","r",stdin);
    rd(n),rd(m),rd(s);
    int x,y,z;
    inc(i,1,m)
    {
        rd(x),rd(y),rd(z);
        add(x,y,z);
    }
    
    spfa();
    
    inc(i,1,n)printf("%lld ",dis[i]);
    re 0;
}

dijsktra

单源最短路
无负边

#include<bits/stdc++.h>
#define re return
#define inc(i,l,r) for(int i=l;i<=r;++i)
using namespace std;
template<typename T>inline void rd(T&x)
{
    char c;bool f=0;
    while((c=getchar())<'0'||c>'9')if(c=='-')f=1;
    x=c^48;
    while((c=getchar())>='0'&&c<='9')x=x*10+(c^48);
    if(f)x=-x;
}

const int maxn=1e4+5,maxm=5e5+5;
int n,m,hd[maxn];
struct node{
    int to,nt,val;
}e[maxm<<1];
int k,s;
inline void add(int x,int y,int z){
    e[++k]=(node){y,hd[x],z};hd[x]=k;
}

#define ll long long
ll inf=2147483647,dis[maxn];
struct KKK{
int x,val;
inline bool operator<(KKK u)const 
{
    re val>u.val;
}
};
inline void dij()
{
    inc(i,1,n)dis[i]=inf;
    dis[s]=0;
    priority_queue<KKK>q;
    q.push((KKK){s,0});
    while(!q.empty())
    {
        KKK u=q.top();
        q.pop();
        int x=u.x;
        if(dis[x]!=u.val)continue;
        for(int i=hd[x];i;i=e[i].nt)
        {
            int v=e[i].to;
            if(dis[v]>dis[x]+e[i].val)
            {
                dis[v]=dis[x]+e[i].val;
                q.push((KKK){v,dis[v]});
            }
        }
    }
}

int main()
{
    //freopen("a.in","r",stdin);
    rd(n),rd(m),rd(s);
    int x,y,z;
    inc(i,1,m)
    {
        rd(x),rd(y),rd(z);
        add(x,y,z);
    }
    
    dij();
    
    inc(i,1,n)printf("%lld ",dis[i]);
    re 0;
}

floyd

O(n^3)
多源最短路

#include<bits/stdc++.h>
using namespace std;
#define inf 1234567890
#define maxn 10005
inline int read()
{
    int x=0,k=1; char c=getchar();
    while(c<'0'||c>'9'){if(c=='-')k=-1;c=getchar();}
    while(c>='0'&&c<='9')x=(x<<3)+(x<<1)+(c^48),c=getchar();
    return x*k;
}//快读
int a[maxn][maxn],n,m,s;
inline void floyd()
{
    for(int k=1;k<=n;k++)
    //这里要先枚举k（可以理解为中转点）
	{
        for(int i=1;i<=n;i++)
		{
            if(i==k||a[i][k]==inf)
            {
                continue;
			}
			for(int j=1;j<=n;j++)
			{
                a[i][j]=min(a[i][j],a[i][k]+a[k][j]);
                //松弛操作，即更新每两个点之间的距离
                //松弛操作有三角形的三边关系推出
                //即两边之和大于第三边
            }
        }
    }
}
int main()
{
    n=read(),m=read(),s=read();
    for(int i=1;i<=n;i++)
	{
        for(int j=1;j<=n;j++)
		{
            a[i][j]=inf;
        }
    }
	//初始化，相当于memset(a,inf,sizeof(a))
    for(int i=1,u,v,w;i<=m;i++)
	{
        u=read(),v=read(),w=read();
        a[u][v]=min(a[u][v],w);
        //取min可以对付重边
    }
    floyd();
    a[s][s]=0;
    for(int i=1;i<=n;i++)
    {
        printf("%d ",a[s][i]);
    }
    return 0;
}

二、动态规划

dp数学建模的应用不多，感觉主要还是各种环境下的一个背包（多维dp），对于状压，数位都不怎么涉及
总的思想来说偏向背包较为单一，找递归方程时的问题主要在于结合其他信息，可能涉及到概率（马尔科夫链），图（偏向树形dp之类的）

  1. 背包
    采药
    一维
#include<bits/stdc++.h>
using namespace std;
int a[100001];
int o;
int main()
{
	int t,m;
	cin>>t>>m;
int w[m+1],v[m+1];
for(int i=1;i<=m;i++)
cin>>w[i]>>v[i];
	
	for(int j=1;j<=t;j++)	
	for(int k=1;k<=m;k++)
		{
		    a[j]=o;
		    if(j>=w[k])
		    {a[j]=max(a[j],a[j-w[k]]+v[k]); 
		    o=max(o,a[j]);}
		}
			
	cout<<a[t];
	return 0;
}

二维

#include<bits/stdc++.h>
using namespace std;
int a[101][1001];
int main()
{
int n,m;
cin>>n>>m;
int w[m+1];
int v[m+1];
for(int i=1;i<=m;i++)
cin>>w[i]>>v[i];

for(int i=1;i<=m;i++)
for(int j=1;j<=n;j++)
{ a[i][j]=a[i-1][j];
if(j>=w[i])a[i][j]=max(a[i-1][j-w[i]]+v[i],a[i][j]); 

}
cout<<a[m][n];
return 0;
}

2.树形dp
在连通图上dp
没有上司的舞会

#include<bits/stdc++.h>
using namespace std;
int f[6005][3],head[6005],cc[6005],in[6005];
int n,a,b,c;

void dfs(int x)
{   
	for(int i=head[x];i!=0;i=cc[i])
 	{	
 	  dfs(i);
	 f[x][1]=f[x][1]+f[i][0];
	 f[x][0]+=max(f[i][0],f[i][1]);
	}
}

int main()
{  

scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%d",&f[i][1]);

for(int i=1;i<n;i++)
{scanf("%d%d",&a,&b); 
cc[a]=head[b];
head[b]=a;in[a]=1;}

for(int i=1;i<=n;i++)
if(in[i]==0){c=i;break;}
dfs(c);
printf("%d",max(f[c][1],f[c][0]));

return 0;
}

三、启发式算法

模拟退火
模拟退火算法（Simulate Anneal，SA）是一种通用概率演算法，用来在一个大的搜寻空间内找寻命题的最优解。
https://www.cnblogs.com/flashhu/p/8884132.html文章来源地址https://www.toymoban.com/news/detail-609899.html

#include<bits/stdc++.h>
#define re return
#define st static
#define mem(a,b) memset((a),(b),sizeof(a))
#define inc(i,l,r) for(register int i=l;i<=r;++i)
#define dec(i,l,r) for(register int i=l;i>=r;--i)

using namespace std;
int n,x[1005],y[1005],w[1005];
double EPS=10e-15,D=0.975;

double calc(double x0,double y0)
{
	double res=0;
	inc(i,1,n)res+=sqrt((x[i]-x0)*(x[i]-x0)+(y[i]-y0)*(y[i]-y0))*w[i];
	re res;
}

int main()
{
//	freopen("in.txt","r",stdin);
	double x1=0,y1=0,x0,y0,bx,by,res,ans,best,time=2;
	scanf("%d",&n);
	inc(i,1,n){
		scanf("%d%d%d",&x[i],&y[i],&w[i]);
		bx+=x[i];by+=y[i];
	}
	
	best=calc(bx/=n,by/=n);//用平均值作为最初解
	srand(20130317);
	while(time--)
	{
		x1=bx,y1=by,ans=best;
		for(double T=100000;T>EPS;T*=D)
		{
			x0=x1+T*(2*rand()-RAND_MAX);y0=y1+T*(2*rand()-RAND_MAX);
			res=calc(x0,y0);
			if(res<best){best=res;bx=x0;by=y0;}
			if(res<ans||exp((ans-res)/T)>(double)(rand())/RAND_MAX)
			{ans=res;x1=x0;y1=y0;}
		}
	}
	printf("%.3lf %.3lf",bx,by);
	re 0;
}

到了这里，关于最优化方法的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处： 如若内容造成侵权/违法违规/事实不符，请点击违法举报进行投诉反馈，一经查实，立即删除！

分享到：
领支付宝红包 赞助服务器费用

相关文章

  • 最优化：建模、算法与理论（最优性理论2

    最优化：建模、算法与理论（最优性理论2

    考虑优化问题 min ⁡ x ∈ R n 1 2 ∣ ∣ x − y ∣ ∣ 2 2 , s . t . A x = b min_{x{in}R^n}frac{1}{2}||x-y||_2^2,\\\\ s.t.{quad}Ax=b x ∈ R n min ​ 2 1 ​ ∣∣ x − y ∣ ∣ 2 2 ​ , s . t . A x = b 其中 A ∈ R m × n , b ∈ R m , y ∈ R n A{in}R^{m times n},b{in}R^m,y{in}R^n A ∈ R m × n , b ∈ R m , y ∈ R n 为给定的矩阵

    2024年02月07日
    浏览(43)
  • 图论第一次作业（教材：图论与网络最优化算法龚劬编著）

    图论第一次作业（教材：图论与网络最优化算法龚劬编著）

    5.证明K维超立方体 的顶点是 ，边数是 ，且是二部图，其中， 的顶点集 ，且两顶点相邻当且仅当着两个k维序列正好有一对应项不相同。 8.任何两个以上的人组成的人群中，至少有两个人，他们的朋友数一样多。 11.设 是平面上的点集，其中任意两点间的距离至少是1，证明：

    2024年02月08日
    浏览(42)
  • 最优化：建模、算法与理论（典型优化问题

    最优化：建模、算法与理论（典型优化问题

    4.1.1 基本形式和应用背景 再次说明一下，其实这本书很多的内容之前肯定大家都学过，但是我觉得这本书和我们之前学的东西的出发角度不一样，他更偏向数学，也多一个角度让我们去理解 线性规划问题的一般形式如下： min ⁡ x ∈ R n c T x s . t . A x = b G x ≤ e (4.1.1) min_{x{

    2024年02月09日
    浏览(250)
  • 数学学习——最优化问题引入、凸集、凸函数、凸优化、梯度、Jacobi矩阵、Hessian矩阵

    数学学习——最优化问题引入、凸集、凸函数、凸优化、梯度、Jacobi矩阵、Hessian矩阵

    例如：有一根绳子，长度一定的情况下，需要如何围成一个面积最大的图像？这就是一个最优化的问题。就是我们高中数学中最常见的最值问题。 最优化问题的一般形式是： m i n ​ f ( x ) x ∈ C min​f(x) \\\\ x in C min ​ f ( x ) x ∈ C 其中， f f f 是目标函数， A A A 是约束条件，

    2024年02月15日
    浏览(42)

  • 机器学习笔记之最优化理论与方法(一)最优化问题概述

    从本节开始，将对 最优化理论与方法 进行简单认识。 无论是 最优化理论 还是 最优化方法 ，讨论的 对象 都是 最优化问题 。 关于 最优化问题 的一种简单描述：最优化问题本质上属于 决策问题 。 例如 路径选择 问题：确定达到目的地最佳路径的计量标准 。其中问题的 目

    2024年02月11日
    浏览(45)
  • （最优化理论与方法）第一章最优化简介-第二节：最优化典型实例之稀疏优化和低秩矩阵恢复

    （最优化理论与方法）第一章最优化简介-第二节：最优化典型实例之稀疏优化和低秩矩阵恢复

    考虑下面线性方程组的求解问题，其中 x ∈ R n , b ∈ R m xin R^{n},bin R^{m} x ∈ R n , b ∈ R m ，矩阵 A ∈ R m × n Ain R^{m×n} A ∈ R m × n ，且向量 b b b 的维数远小于向量 x x x 的维数，也即 m m m n n n A x = b Ax=b A x = b 在相关问题中，当我们建立这样的模型后，常常希望 解出向量

    2024年02月08日
    浏览(45)
  • 无约束最优化方法

    无约束最优化方法

    求解无约束最优化的基本思路 给定初始点 x 0 ∈ R n , k = 0 x_0in mathbb{R}^n,k=0 x 0 ​ ∈ R n , k = 0 判断当前解是否满足终止准则，若满足则停止迭代，若不满足则转3. 确定 f ( x ) f(x) f ( x ) 在 x k x_k x k ​ 点的下降方向 确定步长 λ k lambda_k λ k ​ ，使 f ( x k + λ k d k ) f(x_k+lambda_

    2023年04月08日
    浏览(96)
  • 最优化方法

    最优化方法

    1.最小生成树 图的生成树是它的一颗含有其所有顶点的无环连通子图,一 幅加权图的最小生成树(MST)是它的一颗权值(树中的所有边的权值之和) 最小的生成树 • 适用场景：道路规划、通讯网络规划、管道铺设、电线布设等 题目数据 kruskal算法 稀疏图，按边大小排序 prim 稠密图

    2024年02月15日
    浏览(36)

  • 张益唐：数学的浪漫 —— 人工智能的很多东西实际上就是一种最优化问题

    张益唐，美国加州大学圣塔芭芭拉分校数学系终身教授。张益唐的研究方向是数论。2013年4月17日，他在《数学年刊》发表 《质数间的有界间隔》 ，在 孪生素数猜想 这一数论重大难题上取得重要突破。2022年，张益唐表示，在本质上，他已经证明了朗道-西格尔零点猜想，引发

    2024年02月07日
    浏览(51)

  • 【人工智能的数学基础】多目标优化的帕累托最优(Pareto Optimality)

    寻找多目标优化问题的帕累托最优解. paper：

    2024年02月07日
    浏览(38)

觉得文章有用就打赏一下文章作者

支付宝扫一扫打赏

博客赞助

微信扫一扫打赏

请作者喝杯咖啡吧~博客赞助

支付宝扫一扫领取红包，优惠每天领

二维码1

领取红包

二维码2

领红包