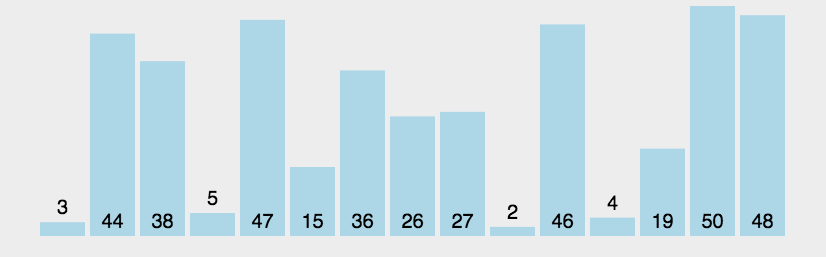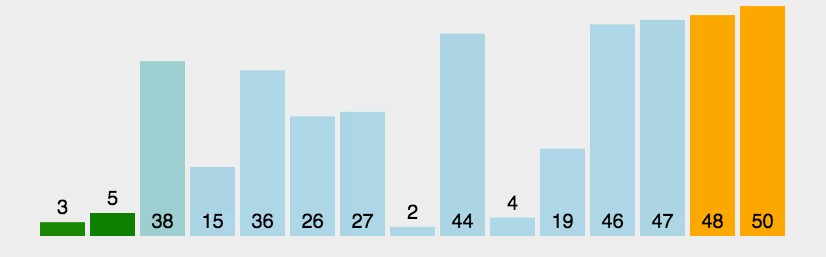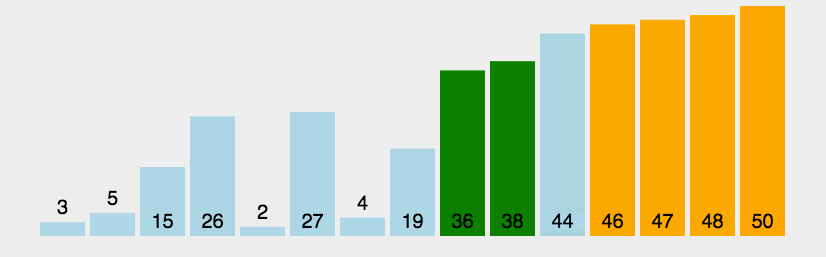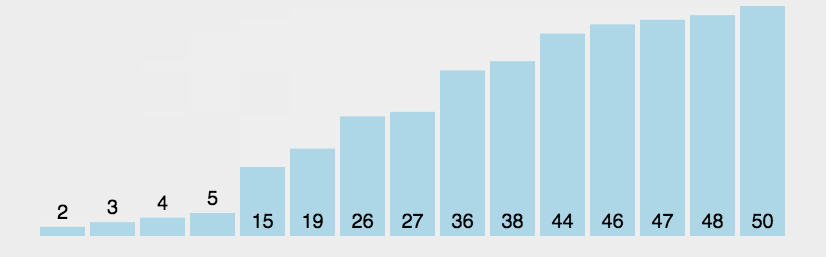Java语言常用的算法

Java语言常用的算法包括：

1. 排序算法：冒泡排序、选择排序、插入排序、希尔排序、归并排序、快速排序、堆排序等。

2. 查找算法：顺序查找、二分查找、哈希查找等。

3. 字符串匹配算法：暴力匹配、KMP算法、Boyer-Moore算法等。

4. 图论算法：最短路径算法、最小生成树算法、拓扑排序等。

5. 动态规划算法：背包问题、最长公共子序列、最长上升子序列等。

6. 贪心算法：最小生成树、单源最短路径等。

7. 分治算法：快速排序、归并排序等。

8. 网络流算法：最大流问题、最小割问题等。

9. 数学算法：欧几里得算法、素数判断、大数计算等。

以上仅是Java语言中常用的一些算法，还有很多其他的算法可以应用于Java开发中。

下面我将为您介绍一些Java常用算法，并提供相应的代码示例。

1. 排序算法

排序算法是计算机科学中的一种基本算法，它可以将一组数据按照一定的顺序排列。常见的排序算法有冒泡排序、选择排序、插入排序、归并排序、快速排序、堆排序等。这些算法的复杂度不同，有些是稳定排序，有些不是，也有些适用于小规模数据，有些适用于大规模数据。

1.1 冒泡排序
冒泡排序是最简单的排序算法之一，其基本思想是将相邻的两个元素进行比较，如果顺序不对就交换它们的位置。该算法的时间复杂度为O(n^2)。

public static void bubbleSort(int[] arr) {
    int n = arr.length;
    for (int i = 0; i < n - 1; i++) {
        for (int j = 0; j < n - i - 1; j++) {
            if (arr[j] > arr[j + 1]) {
                int temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
            }
        }
    }
}

1.2 选择排序
选择排序的基本思想是每次选择未排序序列中最小的元素，将其放到已排序序列的末尾。该算法的时间复杂度也为O(n^2)。

public static void selectionSort(int[] arr) {
    int n = arr.length;
    for (int i = 0; i < n - 1; i++) {
        int minIndex = i;
        for (int j = i + 1; j < n; j++) {
            if (arr[j] < arr[minIndex]) {
                minIndex = j;
            }
        }
        int temp = arr[i];
        arr[i] = arr[minIndex];
        arr[minIndex] = temp;
    }
}

1.3 插入排序
插入排序的基本思想是将未排序序列中的每个元素插入到已排序序列的合适位置。该算法的时间复杂度也为O(n^2)。

public static void insertionSort(int[] arr) {
    int n = arr.length;
    for (int i = 1; i < n; i++) {
        int key = arr[i];
        int j = i - 1;
        while (j >= 0 && arr[j] > key) {
            arr[j + 1] = arr[j];
            j--;
        }
        arr[j + 1] = key;
    }
}

1.4 快速排序
快速排序的基本思想是选择一个基准元素，将序列分成两部分，一部分元素比基准元素小，一部分元素比基准元素大，然后分别对这两部分进行快速排序。该算法的时间复杂度为O(nlogn)。

public static void quickSort(int[] arr, int left, int right) {
    if (left >= right) {
        return;
    }
    int pivot = arr[left];
    int i = left;
    int j = right;
    while (i < j) {
        while (i < j && arr[j] >= pivot) {
            j--;
        }
        arr[i] = arr[j];
        while (i < j && arr[i] <= pivot) {
            i++;
        }
        arr[j] = arr[i];
    }
    arr[i] = pivot;
    quickSort(arr, left, i - 1);
    quickSort(arr, i + 1, right);
}

2. 查找算法

查找算法，也称为搜索算法，是计算机科学中的一种基本算法，它用于在数据集合中查找特定元素的位置或存在性。常见的查找算法有线性查找、二分查找、哈希查找等。

2.1 二分查找
二分查找，也称为折半查找，它要求数据集合必须是有序的，它的基本思想是将数据集合分成两半，如果目标元素比中间元素小，就在前半部分继续查找，否则在后半部分继续查找，直到找到目标元素或数据集合为空。二分查找的时间复杂度为O(logn)。

public static int binarySearch(int[] arr, int target) {
    int left = 0;
    int right = arr.length - 1;
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (arr[mid] == target) {
            return mid;
        } else if (arr[mid] < target) {
            left = mid + 1;
        } else {
            right = mid - 1;
        }
    }
    return -1;
}

2.2 线性查找
线性查找是最简单的查找算法之一，它的基本思想是从数据集合的第一个元素开始逐个比较，直到找到目标元素或遍历完整个数据集合。线性查找的时间复杂度为O(n)。

public class LinearSearch {
    public static int linearSearch(int[] arr, int target) {
        // 遍历整个数组
        for (int i = 0; i < arr.length; i++) {
            if (arr[i] == target) {
                // 找到目标元素，返回索引
                return i;
            }
        }
        // 没有找到目标元素，返回-1
        return -1;
    }

    public static void main(String[] args) {
        int[] arr = {1, 2, 3, 4, 5};
        int target = 3;
        int index = linearSearch(arr, target);
        if (index == -1) {
            System.out.println("目标元素不存在");
        } else {
            System.out.println("目标元素在数组中的位置为：" + index);
        }
    }
}

3. 字符串匹配算法

字符串匹配算法是计算机科学中的一种算法，用于在一个字符串中查找一个子串的出现位置。字符串匹配算法可以应用于文本搜索、数据处理、图形处理等领域。在实际应用中，常用的字符串匹配算法包括暴力匹配算法、KMP算法、Boyer-Moore算法、Rabin-Karp算法等。

3.1 KMP算法
KMP算法，即Knuth-Morris-Pratt算法，是一种高效的字符串匹配算法。它的基本思想是，利用已知信息，尽量减少模式串与文本串的匹配次数。具体实现中，KMP算法利用了前缀和后缀的概念，对模式串进行预处理，以便在匹配过程中快速调整模式串的位置。KMP算法的时间复杂度是O(m+n)，其中m和n分别为模式串和文本串的长度。

public static int kmp(String s, String p) {
    int[] next = getNext(p);
    int i = 0, j = 0;
    while (i < s.length() && j < p.length()) {
        if (j == -1 || s.charAt(i) == p.charAt(j)) {
            i++;
            j++;
        } else {
            j = next[j];
        }
    }
    if (j == p.length()) {
        return i - j;
    } else {
        return -1;
    }
}

private static int[] getNext(String p) {
    int[] next = new int[p.length()];
    next[0] = -1;
    int i = 0, j = -1;
    while (i < p.length() - 1) {
        if (j == -1 || p.charAt(i) == p.charAt(j)) {
            i++;
            j++;
            if (p.charAt(i) != p.charAt(j)) {
                next[i] = j;
            } else {
                next[i] = next[j];
            }
        } else {
            j = next[j];
        }
    }
    return next;
}

4. 图论算法

图论算法主要是用来处理图结构的算法，图结构是由节点（顶点）和边（连接节点的线）构成的。

4.1 Dijkstra算法

public static void dijkstra(int[][] graph, int start) {
    int n = graph.length;
    boolean[] visited = new boolean[n];
    int[] dist = new int[n];
    Arrays.fill(dist, Integer.MAX_VALUE);
    dist[start] = 0;
    for (int i = 0; i < n; i++) {
        int u = -1;
        for (int j = 0; j < n; j++) {
            if (!visited[j] && (u == -1 || dist[j] < dist[u])) {
                u = j;
            }
        }
        visited[u] = true;
        for (int v = 0; v < n; v++) {
            if (graph[u][v] != 0 && !visited[v]) {
                dist[v] = Math.min(dist[v], dist[u] + graph[u][v]);
            }
        }
    }
}

5. 动态规划算法

动态规划算法是一种解决多阶段决策过程最优化问题的数学方法。它的基本思想是将复杂问题分解成若干个简单子问题，并且保存子问题的解，避免重复计算，最终得到原问题的解。

动态规划算法的应用范围非常广泛，例如：

a.最长公共子序列：用于比较两个字符串的相似度。

b.背包问题：求在给定容量和物品重量、价值的情况下，如何选择物品才能使得总价值最大。

c.最短路径问题：Dijkstra算法和Floyd算法就可以用动态规划的思想来解决。

d.编辑距离问题：用于计算两个字符串之间的编辑距离。

e.序列对齐问题：用于比较两个序列的相似度。

f.字符串匹配问题：例如正则表达式匹配问题。

g.图像处理问题：例如图像边缘检测问题。

动态规划算法的优点是可以避免重复计算，使得算法效率更高。但是它的缺点也很明显，那就是需要耗费较多的空间来存储子问题的解。在实际应用中需要权衡利弊，选择合适的算法来解决问题。

5.1 背包问题

public static int knapsack(int[] weight, int[] value, int capacity) {
    int n = weight.length;
    int[][] dp = new int[n + 1][capacity + 1];
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= capacity; j++) {
            if (j >= weight[i - 1]) {
                dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i - 1]] + value[i - 1]);
            } else {
                dp[i][j] = dp[i - 1][j];
            }
        }
    }
    return dp[n][capacity];
}

6. 贪心算法

贪心算法是一种基于贪心策略的算法，它的基本思想是通过局部最优解来推导全局最优解。贪心算法通常采用贪心策略来进行问题求解，即在每个阶段选择当前状态下最优的解决方案，而不考虑后续的影响。

贪心算法的应用范围非常广泛，例如：

a.最小生成树：Prim算法和Kruskal算法就是基于贪心思想来求解最小生成树问题的。

b.单源最短路径问题：Dijkstra算法就是基于贪心思想来求解单源最短路径问题的。

c.背包问题：虽然动态规划算法也可以解决背包问题，但是贪心算法通常也可以得到较优解。

d.哈夫曼编码问题：用于数据压缩中，通过构造哈夫曼树来实现数据压缩。

e5.区间覆盖问题：例如求解最少需要几个区间才能覆盖一个线段的问题。

f.任务调度问题：例如在有限的时间内，如何安排多个任务的执行顺序，才能使得任务的完成时间最短。

贪心算法的优点是求解速度快，通常比其他算法效率高。但是贪心算法的缺点也很明显，那就是无法保证得到最优解，只能得到一个较优解。在实际应用中需要根据具体问题选择合适的算法来解决。

6.1 零钱兑换

public static int coinChange(int[] coins, int amount) {
    Arrays.sort(coins);
    int ans = 0;
    for (int i = coins.length - 1; i >= 0; i--) {
        if (amount == 0) {
            break;
        }
        if (coins[i] <= amount) {
            int count = amount / coins[i];
            ans += count;
            amount -= count * coins[i];
        }
    }
    if (amount != 0) {
        ans = -1;
    }
    return ans;
}

7. 分治算法

分治算法是一种递归的算法思想，其基本思想是将一个大问题分解为若干个小问题，分别解决这些小问题，最后将小问题的解合并起来得到大问题的解。通常情况下，分治算法的效率很高，因为它能够避免重复计算，而且能够充分利用多核处理器的并行处理能力。

分治算法通常分为三个步骤：

分解：将原问题分解成若干个规模较小、相互独立且与原问题性质相同的子问题。

解决：递归地求解各个子问题。当子问题的规模足够小时，直接求解。

合并：将各个子问题的解合并成原问题的解。

经典的分治算法有很多，比如快速排序、归并排序、二分查找等等。在实际应用中，分治算法也可以用来解决很多实际问题，比如在计算机图形学中，将一个大的图形对象分解成若干个小的三角形对象，每个小对象单独处理后再合并成一个大对象。

7.1 归并排序

public static void mergeSort(int[] arr, int left, int right) {
    if (left >= right) {
        return;
    }
    int mid = left + (right - left) / 2;
    mergeSort(arr, left, mid);
    mergeSort(arr, mid + 1, right);
    int[] temp = new int[right - left + 1];
    int i = left, j = mid + 1, k = 0;
    while (i <= mid && j <= right) {
        if (arr[i] <= arr[j]) {
            temp[k++] = arr[i++];
        } else {
            temp[k++] = arr[j++];
        }
    }
    while (i <= mid) {
        temp[k++] = arr[i++];
    }
    while (j <= right) {
        temp[k++] = arr[j++];
    }
    System.arraycopy(temp, 0, arr, left, temp.length);
}

8. 网络流算法

网络流算法是一类用来解决网络流问题的算法，其中最著名的算法是最大流算法。网络流问题是指在一个有向图中，每条边都有一个容量限制，同时给定一个源点和汇点，要求从源点到汇点找到一条最大流的路径，使得经过这条路径的总流量最大。

最大流算法的基本思想是从源点开始，沿着增广路径不断增加流量，直到无法再找到增广路径为止。增广路径是指一条从源点到汇点的路径，其上所有边的剩余容量都大于零。为了寻找增广路径，最大流算法使用了广度优先搜索、深度优先搜索等算法。

除了最大流算法，还有一些其他的网络流算法，比如最小割算法、费用流算法等等。这些算法都是基于网络流问题的基本概念和原理，通过不同的算法思想和技巧来解决不同的网络流问题。网络流算法在实际应用中有很多应用，比如在电力系统中，用来优化电力网络的输电能力；在运输规划中，用来优化货物的运输方案等等。

8.1 最大流

public static int maxFlow(int[][] graph, int s, int t) {
    int n = graph.length;
    int[][] res = new int[n][n];
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            res[i][j] = graph[i][j];
        }
    }
    int[] parent = new int[n];
    int maxFlow = 0;
    while (bfs(res, s, t, parent)) {
        int pathFlow = Integer.MAX_VALUE;
        for (int v = t; v != s; v = parent[v]) {
            int u = parent[v];
            pathFlow = Math.min(pathFlow, res[u][v]);
        }
        for (int v = t; v != s; v = parent[v]) {
            int u = parent[v];
            res[u][v] -= pathFlow;
            res[v][u] += pathFlow;
        }
        maxFlow += pathFlow;
    }
    return maxFlow;
}

private static boolean bfs(int[][] graph, int s, int t, int[] parent) {
    int n = graph.length;
    boolean[] visited = new boolean[n];
    Queue<Integer> queue = new LinkedList<>();
    queue.offer(s);
    visited[s] = true;
    parent[s] = -1;
    while (!queue.isEmpty()) {
        int u = queue.poll();
        for (int v = 0; v < n; v++) {
            if (!visited[v] && graph[u][v] > 0) {
                queue.offer(v);
                visited[v] = true;
                parent[v] = u;
            }
        }
    }
    return visited[t];
}

9. 数学算法

数学算法是指在数学领域中用来解决问题的一类算法，它们通常涉及到一些高级的数学概念和技巧。数学算法在计算机科学、物理学、工程学、统计学等领域都有广泛的应用，比如在密码学中用来加密和解密数据、在计算机图形学中用来进行几何变换和图形优化、在金融学中用来进行风险分析和投资决策等等。

常见的数学算法有很多，以下是其中几个例子：

求解方程和方程组的算法，如高斯消元法、迭代法等。

最优化问题的算法，如线性规划、非线性规划等。

数值积分和微分的算法，如辛普森法、龙格-库塔法等。

离散数学的算法，如图论、组合数学等。

概率和统计的算法，如蒙特卡罗方法、马尔可夫链蒙特卡罗方法等。

这些数学算法都是基于不同的数学原理和概念，通过不同的算法思想和技巧来解决不同的数学问题。在实际应用中，选择适当的数学算法可以大大提高计算效率和准确性，因此数学算法在科学计算、数据分析、金融投资等领域都有着广泛的应用。

9.1 素数判断

public static boolean isPrime(int n) {
    if (n <= 1) {
        return false;
    }
    for (int i = 2; i * i <= n; i++) {
        if (n % i == 0) {
            return false;
        }
    }
    return true;
}

以上就是Java常用算法的一些示例代码，希望对您有所帮助。文章来源地址https://www.toymoban.com/news/detail-610304.html

到了这里，关于Java语言常用的算法的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！