0 图的应用
1 生成树
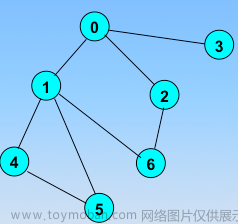
生成树：所有顶点均由边连接在一起，但不存在回路的图。
也就是两个条件，顶点条件和边数条件，顶点都要保持连通，边数达到最少，没有回路。
如右边的图，随便再加一条边就有回路了。
所有生成树都具有以下的共同特点：
- 生成树的顶点个数与图的顶点个数相同；
- 生成树是图的极小连通子图，去掉一条边则非连通；
- 一个有 n n n个顶点的连通图的生成树有 n − 1 n-1 n−1条边；
- 生成树中任意两个顶点间的路径是唯一的；
- 含有
n
n
n个顶点
n
−
1
n-1
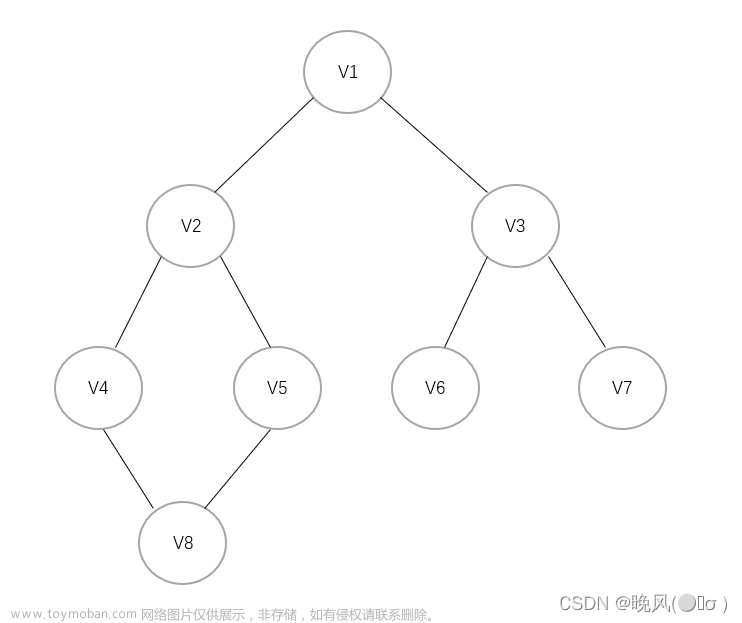
n−1条边的图不一定是生成树，如下图所示
因为生成树是连通的，每个顶点都要用边相连，上图是不连通的，有两个连通分量。
1.1 无向图的生成树
生成树要包含所有顶点，那么对图进行遍历，把走过的边全部加入到图当中。
遍历则采用DFS与BFS都可以。
用DFS生成的生成树就是DFS生成树。
用BFS生成的生成树就是BFS生成树。
综上
1.2 最小生成树
最小生成树：给定一无向网络在该网的所有生成树中，使得各边权值之和最小的那棵生成树称为该网的最小生成树，也叫最小代价生成树。
最小生成树可能是不唯一的。
1.2.1 构造最小生成树
构造最小生成树的算法很多，其中多数算法都利用了MST(Minimum Spanning Tree)的性质。
MST性质：
其实就是贪心算法，不断去找权值最小的边。
设
N
=
(
V
,
E
)
N=(V, E)
N=(V,E)以目是一个连通网，
U
U
U是顶点集
V
V
V的一个非空子集。若边
(
u
,
v
)
(u, v)
(u,v)是一条具有最小权值的边，其中
u
∈
U
,
v
∈
V
−
U
u∈U,v∈V-U
u∈U,v∈V−U则必存在一棵包含边
(
u
,
v
)
(u,v)
(u,v)的最小生成树。
举例
现在
U
=
{
v
1
}
U=\{v_1\}
U={v1}，所以
V
−
U
=
{
v
2
,
v
3
,
v
4
,
v
5
,
v
6
}
V-U=\{v_2,v_3,v_4,v_5,v_6\}
V−U={v2,v3,v4,v5,v6}，所以
u
∈
U
,
v
∈
V
−
U
u∈U,v∈V-U
u∈U,v∈V−U当中，其中从
v
1
v_1
v1到
v
3
v_3
v3是最小的，权值为1，存在这个权值最小的边，这条边一定会包含在某个最下生成树当中。
1.2.2 Prim算法构造最小生成树
算法思想：
1.2.3 Kruskal算法构造最小生成树
相比Prim算法更加贪心，直截了当贪心，前提不成环。这次开始就把所有顶点都加入到最小生成树上面去。不过并不包括边，这时边的集合都是空集，没包含边，彼此之间不连通。
然后直接在边集合当中选权值最小的边，直接加入。
以此类推，选到所有顶点都连通为止（前提不能形成回路）（n个点，n-1条边）。
1.2.4 两种算法的比较
Prim是选择点加入的，而Kruskal是选择边的。选择边的时候和顶点数是没关系的。
1.3 最短路径
1.3.1 两点间最短路径
从起点走向终点，并非要n个节点都包括，也并非要n-1条边。
直到找到路径长度最短的一条路径。
这种最短路径也称为单源的最短路径，采用Dijkstra算法。
1.3.2 某源点到其他各点最短路径
所有顶点的最短路径，统一使用Floyd弗洛伊德算法。
1.3.3 Dijkstra
其时间复杂度为
O
(
n
3
)
O(n^3)
O(n3)
按照路径长度递增次序产生最短路径，启发式贪心算法。
启发式算法，先找最短的，后面再及时更新，具体过程可以看王老师的视频。
1.3.4 Floyd
其时间复杂度为 O ( n 3 ) O(n^3) O(n3)
算法思想：
- 逐个顶点试探
- 从少，到的所有可能存在的路径中
- 选出一条长度最短的路径
求最短路径的步骤：
初始时设置一个
n
n
n阶方阵，令其对角线元素（到自身的路径）为0，若存在弧
<
v
i
,
v
j
>
<v_i, v_j>
<vi,vj>，则对应元素为权值；否则为
∞
∞
∞。
逐步试着在原直接路径中增加中间顶点，若加入中间顶点后路径变短，则修改之；否则，维持原值。所有顶点试探完毕，算法结束。
1.4 拓扑排序
1.4.1 有向无环图DAG
AOV网以顶点表示活动；AOE网用弧表示活动（子工程）。
AOV网用来解决拓扑排序，AOE网用来解决关键路径问题。
拓扑排序的一个小例子：
1.4.2 AOV网
问题：如何判断AOV网中是否存在回路？
答：
所有顶点都能加入拓扑排序的话，就一定没有网。
拓扑排序。
将网变成一个线性序列的过程就是拓扑排序。
拓扑排序的步骤：
- 首先构建好AOV网
- 在有向图中选一个没有前驱的顶点且输出（例如C1和C9）
- 假设选了C1，在有向图当中删除该顶点和所有以它为尾的弧（C1发出的弧）（即C1与C2，C4，C12的弧）
- 重复上述两步，直至全部顶点均已输出；或者当图中不存在无前驱的顶点为止
1.5 关键路径
制定计划，查找关键路径。
关键路径就是从源点到汇点路径长度（权值之和）最长（大）的路径。
按照任务需求，构建有权图。
举例：
对于上方AOE网，我们关心两个问题：
- 完成整项女程至少需要多少时间？
- 哪些活动是影响工程进度的关键？
以上答为关键路径与路径长度。文章来源：https://www.toymoban.com/news/detail-611500.html
1.5.1 求解关键路径
四个有用的量：
求关键路径的步骤：
文章来源地址https://www.toymoban.com/news/detail-611500.html
到了这里，关于DSA之图（4）：图的应用的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
