多重背包问题——单调队列优化-Toy模板网

这篇具有很好参考价值的文章主要介绍了多重背包问题——单调队列优化。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

一、多重背包问题

我们在之前的文章中曾经讲解过多重背包问题，当时我们讲解了两种方法，一种方法就是三重循环，这种方法最为朴素好想。但是这种方法的时间复杂度非常高，后来我们想到了二进制优化的方式。那么今天我们将再介绍一种更好的优化方式——单调队列优化。

在讲解这种优化方式之前，建议大家先去看看作者之前对另外两种方法的讲解，传送门：多重背包问题（详解二进制优化原理）

二、单调队列优化

1、思路

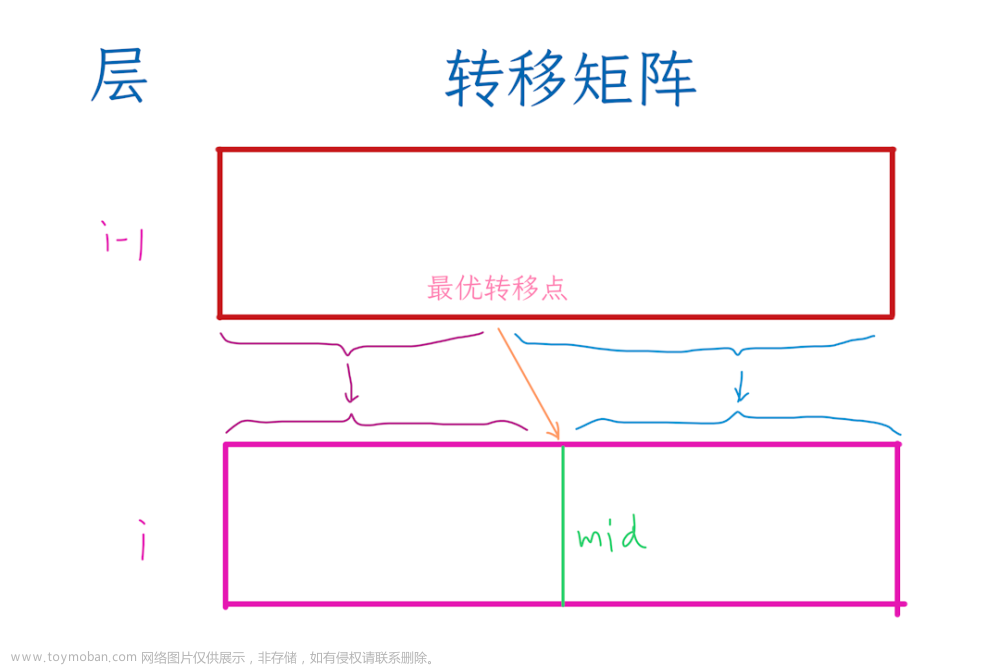
我们观察一下多重背包问题中的转移方程，如下图所示：
单调队列优化多重背包,# DP与贪心题目,算法
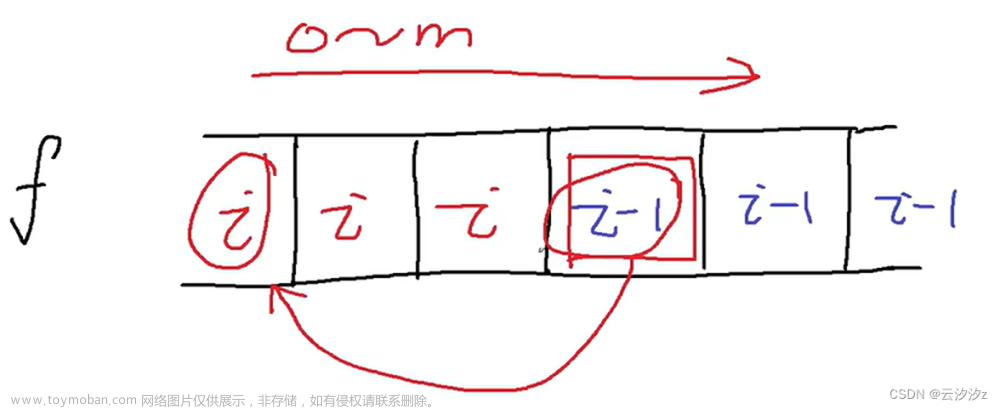
我们发现j,j-v等等都是同余于v的。也就是说，我们的转移方程只会用到余数相等的状态。基于这个观点，我们将容量从0–m按照余数分类。
就像图中的黑色笔记。

那么对于任意一个状态，在容量允许的条件下，我们会向前数s个，（s是物品的个数，这里最多数s个，如果容量装不下了就会小于s个）。然后我们在这s个余数相同的状态中选出一个最大值。如图中的红色框所示。我们可以将这个框看作一个滑动窗口，因为随着图中系数y的增加，这个窗口也在向右移动，即滑动。

那么我们如何构造这个滑动窗口呢？

我们刚刚将0到m之间的数字按照余数分为了若干组，那么现在我们拿出一组写成转移方程，观察一下如何构造滑动窗口。如下图所示：
单调队列优化多重背包,# DP与贪心题目,算法
我们的单调队列存储的是下标，也就是说下标对应着一个固定的状态值。但我们看图中的状态，下标为x的状态所对应的值都不一样。也就是说下标所对的状态都变，既然在变，我们的窗口中的值就很难比较大小。

因此，我们需要经过一个变化，让窗口内下标所对的状态值不变。那么怎么变呢？很简单，我们将后面加的几w提出来。

单调队列优化多重背包,# DP与贪心题目,算法
此时我们就发现，我们max中比较的对象都一致了，这样的话，我们就可以将这些数构造成一个单调减的滑动窗口。

我们还可以观察到，窗口内的状态在不断地-w，但是系数都不同，那么这个系数有什么规律呢？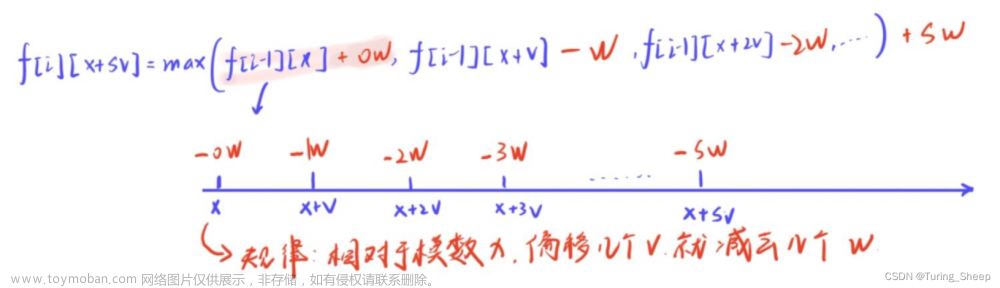
单调队列优化多重背包,# DP与贪心题目,算法知道这个规律的目的在于滑动窗口内元素的比较。比如我们碰到一个新的状态值，我们需要计算出其相对于余数的偏移量然后对这个状态进行减几个w的操作，之后这个值才能放到窗口内。

此时我们将x+sv换成j，因为我们循环中肯定是用j来枚举的，所以换成j来表达易于后面写代码。
单调队列优化多重背包,# DP与贪心题目,算法
但是我们还还有不选这个物品的情况，需要将其加入到队列中，即下图所示，

我们需要利用这个式子判断f[i-1][j]是否有可能是最大值，即将这个数加入队列中。然后我们就可以根据最值更新f[i][j]了，即：

 f[i][j]=f[i-1][q[hh]]+((j-q[hh])/v[i])*w[i];

接下来我们就可以写代码了，按照余数分组，按照偏移量构造队列，选出最值得到当前状态。文章来源地址https://www.toymoban.com/news/detail-611870.html

2、代码

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=1e3+10,M=2e4+10;
int f[N][M],v[N],w[N],s[N],q[M];
int n,m;
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)scanf("%d%d%d",v+i,w+i,s+i);
    for(int i=1;i<=n;i++)
    {
        for(int x=0;x<v[i];x++)
        {
            int hh=0,tt=-1;
            for(int j=x;j<=m;j+=v[i])
            {
                if(hh<=tt&&q[hh]<j-s[i]*v[i])hh++;
                while(hh<=tt&&f[i-1][q[tt]]-(q[tt]-x)/v[i]*w[i]<f[i-1][j]-(j-x)/v[i]*w[i])tt--;
                q[++tt]=j;
                f[i][j]=f[i-1][q[hh]]+((j-q[hh])/v[i])*w[i];
            }
        }
    }
    cout<<f[n][m]<<endl;
    return 0;
}