前置知识:
01背包问题:动态规划之01背包模型_如何何何的博客-CSDN博客
完全背包问题:动态规划之完全背包模型_如何何何的博客-CSDN博客
多重背包问题:动态规划之多重背包模型_如何何何的博客-CSDN博客
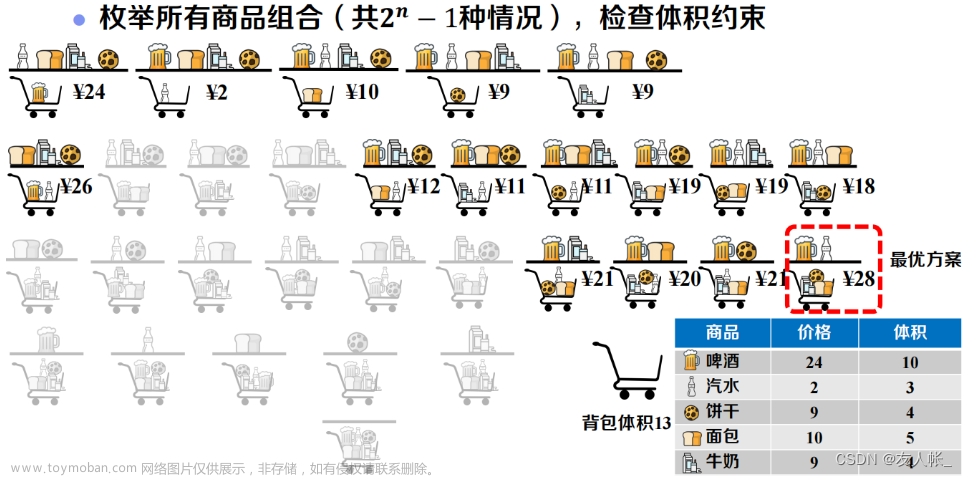
二维费用背包问题:
二维费用即背包问题有两个限制条件。
例题:
有 N 件物品和一个容量是 V 的背包,背包能承受的最大重量是 M;
每件物品只能用一次。体积是 vi,重量是 mi,价值是 wi;
输出最大价值。
输入格式:
第一行三个整数,N,V,M,用空格隔开,分别表示物品件数、背包容积和背包可承受的最大重量;
接下来有 N 行,每行三个整数 vi,mi,wi,用空格隔开,分别表示第 i 件物品的体积、重量和价值。
输出格式:
输出一个整数,表示最大价值。
思路:
该题为二维费用的01背包。f[i][j][k] 表示前 i 个物品,背包体积为 j ,承重为 k 的时候的最大价值;
在01背包基础上加上一重循环即可;
由于n*3的空间太大,所以直接使用空间优化后的01背包。
代码模板如下:
#include<iostream>
using namespace std;
int f[1010][1010];
int N, V, M;
int main() {
cin >> N >> V >> M;
int v, m, w;
for (int i = 0; i < N; i++) {
cin >> v >> m >> w;
for (int j = V; j >= v; j--)
for (int k = M; k >= m; k--)
f[j][k] = max(f[j][k], f[j - v][k - m] + w);
}
cout << f[V][M];
return 0;
}例题1 . 宠物小精灵之收服:
宠物小精灵之收服 - C语言网 (dotcpp.com)
二维费用的 01 背包问题,像普通 01 背包一样做就行,只是加一层循环,最后输出f[n][m](n个球,m个体力),要输出剩下的体力值,遍历f[n][0]~f[n][m]即可。
题目要求当体力为0的时候算抓捕失败,把m-1当做m带入计算即可。
AC代码如下:
#include<iostream>
using namespace std;
const int N=1010;
int f[N][N];
int n,m,k;//拥有的球数和体力值、精灵数
int main(){
cin>>n>>m>>k;
int a,b;//每只精灵需要的球数和照成的伤害
for(int i=0;i<k;i++){//遍历精灵
cin>>a>>b;
for(int j=n;j>=a;j--)//遍历球数
for(int u=m-1;u>=b;u--)//遍历体力
f[j][u]=max(f[j][u],f[j-a][u-b]+1);
}
int tmp=0;
for(int i=m;i>=0;i--)
if(f[n][i]==f[n][m-1])tmp=i;
cout<<f[n][m-1]<<" "<<m-tmp;
}潜水员:
信息学奥赛一本通 T1271-潜水员 - C语言网 (dotcpp.com)
二维费用的 01 背包问题。f[i][j][k] 代表只看前 i 个气缸,氧气至少为 j ,氮气至少为 k 时的最大重量(注意氧气和氮气可以多);
选第i个:
f[i][j][k] = f[i - 1][j - o2[i]][k - n2[i]]不选第i个:
f[i][j][k] = f[i - 1][j][k]。本题要求的是最小值, 每个状态为了不被0影响,需要把所有状态更新为INF,特别的,f[0][0][0]=0;
由于是最少需要的氧气和氮气,所以氮气和氧气超出了也是可以的,相当于背包容量不够了也是可以装当前这个物品的,在更新的时候需要额外更新一些状态,比如我们只需要5的氧气,但是当前物品的氧气为8,我们也是可以选择的,f[i][5][j] = f[i-1][0][j] + w。文章来源:https://www.toymoban.com/news/detail-611954.html
AC代码如下:
#include<iostream>
#include<cstring>
using namespace std;
const int N = 1010;
int f[N][N];//o2,n2
int n, m;//o2,n2
int main() {
cin >> n >> m;
int s, o2, n2, m2;
cin >> s;
memset(f, 0x3f, sizeof f);
f[0][0] = 0;
for (int i = 0; i < s; i++) {
cin >> o2 >> n2 >> m2;
for (int j = n; j >= 0; j--)
for (int k = m; k >= 0; k--)
f[j][k] = min(f[j][k], f[max(j - o2, 0)][max(k - n2, 0)] + m2);
}
cout << f[n][m];
return 0;
}
文章来源地址https://www.toymoban.com/news/detail-611954.html
到了这里,关于动态规划之二维费用的背包模型的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!