0 分类
闭环锁相环技术的主要方案有:
| 类型 | 描述 |
|---|---|
| 1、乘法鉴相器锁相环 | 该锁相环是硬件锁相设计的基础,其基本原理是计算输入信号与输出信号的乘积,经过滤波器和鉴相器输出后,得出输入输出信号的相位差,经过反馈使输出信号锁定输入信号,实现锁相功能。但是这种锁相环为了较好的滤除效果,会降低系统带宽,导致锁相速度受到限制。 |
| 2、单同步坐标系软件锁相环(SSRF-PLL) | 该锁相环技术是软件锁相环技术研究的基础,利用坐标变换和PI控制器,使输出信号跟踪电网电压信号。 |
| 3、基于对称分量的单同步坐标系软件锁相环 | 在 SSRF-PLL 锁相环中加入对称分量法计算方法,达到锁相目的。基本结构中采用了全通滤波器,导致了锁相方法无法达到频率的自适应,其应用领域也受到很大限制。 |
| 4、基于双同步坐标系的解耦软件锁相环(DDSRF-PLL) | 针对三相不平衡电网电压,DDSRF-PLL 主要采用正负序解耦的结构,这种结构能够在电网不平衡时分离电网电压正、负序分量。 |
| 5、基于二阶广义积分软件锁相环(SOGI-PLL) | 针对三相不平衡电网电压,及一些多变的电网电压环境下,SOGI能够在电网不平衡时分离电网电压正、负序分量,同时实现频率跟踪,其锁相精度也高。 |
https://blog.csdn.net/weixin_31054839/article/details/113707862
1、PLL
- 输入为:电网交流电压
- 输出为:同相交流电压、正交信号
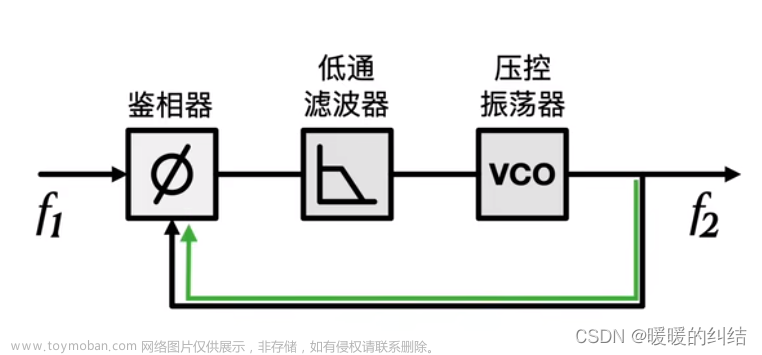
锁相环(phase locked loop)是一种利用相位同步产生的电压,去调谐压控振荡器以产生目标频率的负反馈控制系统。学过自动控制原理的人都知道,这是一种典型的反馈控制电路,利用外部输入的参考信号控制环路内部振荡信号的频率和相位,实现输出信号频率对输入信号频率的自动跟踪,一般用于闭环跟踪电路。是无线电发射中使频率较为稳定的一种方法,主要有VCO(压控振荡器)和PLL IC(锁相环集成电路),压控振荡器给出一个信号,一部分作为输出,另一部分通过分频与PLL IC所产生的本振信号作相位比较,为了保持频率不变,就要求相位差不发生改变,如果有相位差的变化,则PLL IC的电压输出端的电压发生变化,去控制VCO,直到相位差恢复,达到锁相的目的。能使受控振荡器的频率和相位均与输入信号保持确定关系的闭环电子电路。
1.1 系统结构
由三部分构成:我想知道最后反馈的是什么!!!!!
答:最后反馈的是相位,通过使输出相位
θ
\theta
θ控制在目标值wt(也就是输出的wt和输入的wt一直保持一致,那么两者的相位差一直保持为初始相位差),最后达到频率相等,那么最后。
- 鉴相器(PD,Phase Detector)
- 环路滤波器(LF,Loop Filter)
- 压控振荡器(VCO,Voltage Controlled Oscillator)
有的资料在反馈回路中还包括分频器1/N1
| 环节 | 输入 | 输出 |
|---|---|---|
| 鉴相器 | 交流电压 | V d V_d Vd和 V q V_q Vq |
| 环路滤波器(也就是PI环节) | V q V_q Vq | 未知 |
| VCO(也就是积分环节) | 未知 | θ \theta θ |
PLL只是输出到
θ
\theta
θ,其他的都是其他环节处理的了!
最后将
θ
\theta
θ变为PWM波是其他的环节。
总的来说,PLL就是调节输入输出的频差为0的,鉴相器就是通过相乘求得相位差**(还是频差呢?)**;环路滤波器就是积分器,将输入的交流信号积分成直流信号,最后输出VSO的控制电压信号;VCO最后控制频差。
当输入输出相位差恒定时(也就是频率相等),
假设输入信号为:
u
i
(
t
)
=
U
m
s
i
n
[
ω
i
t
+
θ
i
(
t
)
u_i(t)=U_msin[\omega_it+\theta_i(t)
ui(t)=Umsin[ωit+θi(t)
输出信号为:
u
o
(
t
)
=
U
o
m
s
i
n
[
ω
o
t
+
θ
o
(
t
)
u_o(t)=U_omsin[\omega_ot+\theta_o(t)
uo(t)=Uomsin[ωot+θo(t)
式中的
ω
o
\omega_o
ωo为压控振荡器在输入控制电压为零或为直流电压时的振荡角频率,称为电路的固有振荡角频率。
-
模拟乘法器
模拟乘法器的输出电压 u D u_D uD为:

-
低通滤波器LF
低通滤波器LF将上式中的和频分量滤掉,剩下的差频分量作为压控振荡器的输入控制电压 u C ( t ) u_C(t) uC(t)。即 u C ( t ) u_C(t) uC(t)为:
式中的ωi为输入信号的瞬时振荡角频率,θi(t)和θo(t)分别为输入信号和输出信号的瞬时相位。
瞬时相位差θd为:
-
对两边求微分,可得频差的关系式为:

上式等于零,说明锁相环进入相位锁定的状态,此时输出和输入信号的频率和相位保持恒定不变的状态, u C ( t ) u_C(t) uC(t)为恒定值。当上式不等于零时,说明锁相环的相位还未锁定,输入信号和输出信号的频率不等, u C ( t ) u_C(t) uC(t)随时间而变。
输入信号的相位差和LF输出信号关系图 -
VCO
压控振荡器的压控特性如图8-4-3所示,该特性说明压控振荡器的振荡频率ωu以ω0为中心,随输入信号电压uc(t)的变化而变化。该特性的表达式为
ω u ( t ) = ω o + K o u C ( t ) \omega_u(t)=\omega_o+K_ou_C(t) ωu(t)=ωo+KouC(t)
上式说明当 u C ( t ) u_C(t) uC(t)随时间而变时,压控振荡器的振荡频率 ω u \omega_u ωu也随时间而变,锁相环进入“频率牵引”,自动跟踪捕捉输入信号的频率,使锁相环进入锁定的状态,并保持 ω 0 = ω i \omega_0=\omega_i ω0=ωi的状态不变。
https://www.electricaltechnology.org/2019/02/phase-locked-loop-pll.html
https://www.cirmall.com/articles/31424/
https://www.eet-china.com/mp/a119921.html
2、SOGI-based PLL 未完待续
未完待续
[1]杨勇,李世华,朱彬彬,陶雪慧,赵方平,王志冰.基于双阶广义积分的单相光伏并网逆变器灵活功率控制[J].电网技术,2014,38(04):952-958.DOI:10.13335/j.1000-3673.pst.2014.04.020
[1]李永刚,杨雅菲,姜玉霞.弱电网下SOGI-PLL参数对LCL型并网逆变器稳定性影响及参数优化[J].河南理工大学学报(自然科学版),2021,40(04):126-134.DOI:10.16186/j.cnki.1673-9787.2020030094 .
https://liquidsdr.org/blog/pll-howto/
https://imperix.com/doc/implementation/sogi-pll#Simulink-implementation-of-a-SOGI-PLL
2.1 结构理解
首先SOGI只是上文PLL中鉴相器的一部分。
鉴相器:交流电压 =>
V
d
V_d
Vd和
V
q
V_q
Vq
SOGI:交流电压 =>
V
α
V_\alpha
Vα和
V
β
V_\beta
Vβ
因此,SOGI + 【
α
β
\alpha\beta
αβ =>
d
q
dq
dq变换】= 鉴相器
下图中阴影部分为SOGI(Second Oder Generalized Integrator),剩下的部分为滤波器部分。
以及:图xxx
另外一个理解方式为:
1、这个是SOGI的结构
2、这个是基于SOGI实现的带通滤波器。
基于SOGI实现的带通滤波器如图2所示,通过该二阶带通滤波器(BPF),可以实现滤除电网谐波,留下基波分量,同时生成两个相互正交的信号。
https://blog.csdn.net/sinat_40597468/article/details/125582569
2.2 C语言实现
2.2.1 通过控制框图直接实现
1、第一种
x_a=(ualfa_0 - SOGI_ualfa.integral_2)*k_sogi;
SOGI_ualfa.integral_2=SOGI_ualfa.integral_2+w0_sogi*(x_a-SOGI_ualfa.integral_3)*T_ADC;
ualfa_1 = SOGI_ualfa.integral_2;
SOGI_ualfa.integral_3 = SOGI_ualfa.integral_3 + w0_sogi*SOGI_ualfa.integral_2*T_ADC;
ualfa_q = SOGI_ualfa.integral_3;
//参考来源 => https://blog.csdn.net/sinat_40597468/article/details/125582569
其中:ualfa_0对应图xxx中
V
α
V_\alpha
Vα;SOGI_ualfa.integral_2对应图xxx中的
I
2
I_2
I2;SOGI_ualfa.integral_3对应图图xxx中的
I
3
I_3
I3;ualfa_1对应图xxx中的
V
α
′
V _\alpha^{'}
Vα′;ualfa_q对应图xxx中的
q
V
α
′
qV _\alpha^{'}
qVα′;T_ADC为采样时间;
这里:k_sogi=1;w0_sogi = 314.15926;
2、第二种。
这个是包含了SOGI + 后续的
α
\alpha
α、
β
\beta
β转换 + PLL的整个过程。
void PLL(float v_s1)
{
//SOGI正交变换得到两个正交量v1_s(α)、v2_s(β)
v0_s = ((v_s1-v1_s)*K-v2_s)*W;
v1_s += v0_s*Ts;//得到V1(s)(α)
v3_s += v1_s*Ts;
v2_s = v3_s*W;//得到V2(s)(β)
//αβ/dq变换及PI运算
v_q = sin(phase_angle)*(-1)*v1_s + cos(phase_angle)*v2_s;
v_d = <u>cos</u>(phase_angle)*v1_s + sin(phase_angle)*v2_s;//如果不需要就删掉
d_v_q = v_q_ref - v_q;//error
v_q_temp += (d_v_q-d_v_q1) * Kp_PLL + d_v_q * Ki_PLL ;
d_v_q1 = d_v_q;
if(v_q_temp > 20 * pi)
v_q_temp = 20 * pi;
else if(v_q_temp < -20*pi)
v_q_temp = -20 * pi; //用于对误差参数的限幅,防止误差参数过大造成不能输出正常大小的phase_angle最终不能正常进行锁相
//由转速得到相角,并取模
phase_angle += Ts * (100 * pi + v_q_temp);//这里输出的角度是累计误差的角度,同时也是信号当前的角度
if(phase_angle > 2 * pi)
{
phase_angle -= 2 * pi;
}
if(phase_angle < 0)
{
phase_angle += 2 * pi;
}
angles[resultsIndex] = phase_angle;
}
参考来源 => https://zhuanlan.zhihu.com/p/358573305
2.2.2 通过离散SOGI的传递函数来实现
参考来源 => https://www.cnblogs.com/swear/p/12682551.html
2.2.2.1 传递函数
由SOGI的结构图可以得到传递函数:(没有推过,但是好多来源都是这样写的该传递函数)
- 同相传递函数:
H d ( s ) = v ′ v ( s ) = k ω n s s 2 + k ω n s + ω n 2 (1) H_{d}(s)=\frac{v^{\prime}}{v}(s)=\frac{k \omega_{n} s}{s^{2}+k \omega_{n} s+\omega_{n}^{2}} \tag{1} Hd(s)=vv′(s)=s2+kωns+ωn2kωns(1) - 正交信号传递函数:
H q ( s ) = q v ′ v ( s ) = k ω n 2 s 2 + k ω n s + ω n 2 (2) H_{q}(s)=\frac{q v^{\prime}}{v}(s)=\frac{k \omega_{n} ^2}{s^{2}+k \omega_{n} s+\omega_{n}^{2}} \tag{2} Hq(s)=vqv′(s)=s2+kωns+ωn2kωn2(2)
2.2.2.2 离散化
离散化有两种形式:
①利用不同离散化方法的公式来手动离散,从s域 => z域 => 差分方程 来进行离散化;
②利用MATLAB离散。
参考:https://blog.csdn.net/qq_42370406/article/details/127061779?spm=1001.2014.3001.5501
-
手动离散:
离散方法为双线性变换:
s = 2 T s z − 1 z + 1 (3) s=\frac{2}{T_{s}}\frac{z-1}{z+1} \tag{3} s=Ts2z+1z−1(3)
可得,同相传递函数和正交信号传递函数的z域形式为(过程参考该节后面的来源):
H d ( z ) = ( x x + y + 4 ) + ( − x x + y + 4 ) z − 2 1 − ( 2 ( 4 − y ) x + y + 4 ) z − 1 − ( x − y − 4 x + y + 4 ) z − 2 = b 0 + b 2 z − 2 1 − a 1 z − 1 − a 2 z − 2 (7) H_{d}(z)=\frac{\left(\frac{x}{x+y+4}\right)+\left(\frac{-x}{x+y+4}\right) z^{-2}}{1-\left(\frac{2(4-y)}{x+y+4}\right) z^{-1}-\left(\frac{x-y-4}{x+y+4}\right) z^{-2}}=\frac{b_{0}+b_{2} z^{-2}}{1-a_{1} z^{-1}-a_{2} z^{-2}} \tag{7} Hd(z)=1−(x+y+42(4−y))z−1−(x+y+4x−y−4)z−2(x+y+4x)+(x+y+4−x)z−2=1−a1z−1−a2z−2b0+b2z−2(7)
H q ( z ) = ( k ⋅ y x + y + 4 ) + 2 ( k ⋅ y x + y + 4 ) z − 1 + ( k ⋅ y x + y + 4 ) z − 2 1 − ( 2 ( 4 − y ) x + y + 4 ) z − 1 − ( x − y − 4 x + y + 4 ) z − 2 = q b 0 + q b 1 z − 1 + q b 2 z − 2 1 − a 1 z − 1 − a 2 z − 2 (8) H_{q}(z)=\frac{\left(\frac{k \cdot y}{x+y+4}\right)+2\left(\frac{k \cdot y}{x+y+4}\right) z^{-1}+\left(\frac{k \cdot y}{x+y+4}\right) z^{-2}}{1-\left(\frac{2(4-y)}{x+y+4}\right) z^{-1}-\left(\frac{x-y-4}{x+y+4}\right) z^{-2}}=\frac{q b_{0}+q b_{1} z^{-1}+q b_{2} z^{-2}}{1-a_{1} z^{-1}-a_{2} z^{-2}} \tag{8} Hq(z)=1−(x+y+42(4−y))z−1−(x+y+4x−y−4)z−2(x+y+4k⋅y)+2(x+y+4k⋅y)z−1+(x+y+4k⋅y)z−2=1−a1z−1−a2z−2qb0+qb1z−1+qb2z−2(8)
式(7)和式(8)可化简为:
U o ( z ) U i ( z ) = b 0 + b 2 z − 2 1 − a 1 z − 1 − a 2 z − 2 (9) \frac{U_{o}(z)}{U_{i}(z)}=\frac{b_{0}+b_{2} z^{-2}}{1-a_{1} z^{-1}-a_{2} z^{-2}} \tag{9} Ui(z)Uo(z)=1−a1z−1−a2z−2b0+b2z−2(9)
U q o ( z ) U i ( z ) = = q b 0 + q b 1 z − 1 + q b 2 z − 2 1 − a 1 z − 1 − a 2 z − 2 (10) \frac{U_{qo}(z)}{U_{i}(z)}==\frac{q b_{0}+q b_{1} z^{-1}+q b_{2} z^{-2}}{1-a_{1} z^{-1}-a_{2} z^{-2}} \tag{10} Ui(z)Uqo(z)==1−a1z−1−a2z−2qb0+qb1z−1+qb2z−2(10)
根据式(9)和式(10),得同相传递函数和正交信号传递函数的差分方程形式为(过程参考该节后面的来源):
U o ( k ) − a 1 U o ( k − 1 ) − a 2 U o ( k − 2 ) = b 0 U i ( k ) + b 2 U i ( k − 2 ) (11) \ U_{o} (k)-a_{1}U_{o} (k-1)-a_{2}U_{o} (k-2)=b_{0}U_{i}(k)+b_{2}U_{i}(k-2) \tag{11} Uo(k)−a1Uo(k−1)−a2Uo(k−2)=b0Ui(k)+b2Ui(k−2)(11)
U q o ( k ) − a 1 U q o ( k − 1 ) − a 2 U q o ( k − 2 ) = q b 0 U i ( k ) + q b 1 U i ( k − 1 ) + q b 2 U i ( k − 2 ) (12) \ U_{qo} (k)-a_{1}U_{qo} (k-1)-a_{2}U_{qo} (k-2)=qb_{0}U_{i}(k)+qb_{1}U_{i}(k-1)+qb_{2}U_{i}(k-2) \tag{12} Uqo(k)−a1Uqo(k−1)−a2Uqo(k−2)=qb0Ui(k)+qb1Ui(k−1)+qb2Ui(k−2)(12) -
MATLAB离散:
离散代码为:
%%定义s为传递函数
s = tf('s');
%%定义各参数
k = 0.5;
Wn = 100*pi; %%50Hz
Ts = 1e-4; %%10kHz
%%写出传递函数
Hd_s = k*Wn*s/(s^2+k*Wn*s+Wn^2);
Hq_s = k*Wn^2/(s^2+k*Wn*s+Wn^2);
Hd_z = c2d(Hd_s,Ts,'tustin')
Hq_z = c2d(Hq_s,Ts,'tustin')
运行结果:
Hd_z =
0.007791 z^2 - 0.007791
-----------------------
z^2 - 1.983 z + 0.9844
Sample time: 0.0001 seconds
Discrete-time transfer function.
Hq_z =
0.0001224 z^2 + 0.0002448 z + 0.0001224
---------------------------------------
z^2 - 1.983 z + 0.9844
Sample time: 0.0001 seconds
Discrete-time transfer function.
MATLAB离散化的系数为:
2.2.2.3 SOGI的代码实现
无论通过上述两种哪种方式,最后都求得差分方程的系数,因此接下来可以通过代码来进行实现SOGI的结果:
%%
%%函数声明
function [uo,quo] = Orthogonal_Generator(ui,Ts,w,k)
%%
%%定义各中间变量
persistent x;
persistent y;
persistent temp;
persistent b0;
persistent b2;
persistent a1;
persistent a2;
persistent qb0;
persistent qb1;
persistent qb2;
persistent u0; %%代表ui(k)
persistent u1; %%代表ui(k-1)
persistent u2; %%代表ui(k-2)
persistent osg_u0; %%代表uo(k)
persistent osg_u1; %%代表uo(k-1)
persistent osg_u2; %%代表uo(k-2)
persistent osg_qu0; %%代表uqo(k)
persistent osg_qu1; %%代表uqo(k-1)
persistent osg_qu2; %%代表uqo(k-2)
%%
%%初始化各中间变量
if isempty(x) x= 0;
end
if isempty(y) y= 0;
end
if isempty(temp) temp= 0;
end
if isempty(b0) b0= 0;
end
if isempty(b2) b2= 0;
end
if isempty(a1) a1= 0;
end
if isempty(a2) a2= 0;
end
if isempty(qb0) qb0= 0;
end
if isempty(qb1) qb1= 0;
end
if isempty(qb2) qb2= 0;
end
if isempty(u0) u0= 0;
end
if isempty(u1) u1= 0;
end
if isempty(u2) u2= 0;
end
if isempty(osg_u0) osg_u0= 0;
end
if isempty(osg_u1) osg_u1= 0;
end
if isempty(osg_u2) osg_u2= 0;
end
if isempty(osg_qu0) osg_qu0= 0;
end
if isempty(osg_qu1) osg_qu1= 0;
end
if isempty(osg_qu2) osg_qu2= 0;
end
%%
%%各系数赋值
x = 2*k*w*Ts;
y = w*Ts*w*Ts;
temp = 1/(x+y+4.0);
b0 = x*temp;
b2 = (-1.0)*b0;
a1 = (2.0)*(4.0-y)*temp;
a2 = (x-y-4)*temp;
qb0 = (k*y)*temp;
qb1 = qb0*(2.0);
qb2 = qb0;
%%
%%计算过程,对应式11离散序列
u0 = ui;
osg_u0 = (b0*(u0-u2)) + (a1*osg_u1) + (a2*osg_u2);
osg_u2 = osg_u1;
osg_u1 = osg_u0;
%%对应式12离散序列
osg_qu0 = (qb0*u0) + (qb1*u1) + (qb2*u2) + (a1*osg_qu1) + (a2*osg_qu2);
osg_qu2 = osg_qu1;
osg_qu1 = osg_qu0;
%%更新序列值
u2 = u1;
u1 = u0;
%%输出
uo =osg_u0;
quo =osg_qu0;
2.2.2节 通过离散传递函数来实现
参考来源 => https://www.cnblogs.com/swear/p/12682551.html
可以参考:https://blog.csdn.net/qq_42370406/article/details/127061779?spm=1001.2014.3001.5501
2.3 仿真验证
2.3.1 代码验证
对于d轴,
从增益中可以看出:1、观察单个曲线,在基频50Hz 处输出信号,相对于输入信号的相移为0。这也就解释了为什么v’ 与v 同幅同相位;偏离50Hz时,增益会立刻衰减,这也就是为什么利用SOGI能实现滤波的原因。 这种算法能够实现,当输出电压AD 采样存在干扰时,也能够实现准确的dq 分量计算。2、观察多个曲线,k是控制宽带的,k越大,宽带越大。
对于q轴的单个图像:
| 频率 | 增益 | 相位 |
|---|---|---|
| 小于50Hz | 可能放大、不变和衰减 | 滞后,且滞后角度小于90° |
| 50Hz | 1 | 滞后90° |
| 大于50Hz | 衰减 | 滞后,且滞后角度大于90°,小于180° |
对于q轴的多个图像:k控制的是增益放大或衰减的速度,以及相位滞后的程度。k太小,q轴会有宽带,且k越小,宽带越窄。
对于同一组下的dq轴分析(k=0.3,w=2pi50)
从图中,可以发现在42.8Hz时有:
| 名称 | 增益 | 相位 |
|---|---|---|
| d轴 | -3.16dB(衰减为输入幅值的0.695倍,计算公式为10^(-3.16/20)) | 45.4°(超前45.4/360*(1/42.8)=2.947ms) |
| q轴 | -1.73dB(衰减为输入幅值的0.819倍) | -44.4° |
以上表格的内容是通过传递函数算出的,下面将通过simulink的仿真对该数据进行验证。
2.3.2 simulink验证-模块搭建
模型:
输入为50Hz,幅值为10的正弦波时,对于幅值:dq轴两个波形都是10;对于相位:d轴和输入波同相位,q轴滞后d轴90°。
输入为42.8Hz,幅值为10的正弦波时,对于幅值:d轴幅值为6.928,略小于计算值6.95,q轴幅值为8.094,略小于计算值8.19。
对于相位:d轴超前输入波形2.93ms,为45.15°(计算公式为2.93×0.001÷(1/42.8) ×360),略小于计算值45.4°。d轴滞后输入波形2.87ms,为-44.22°,略低于计算值-44.4°。

2.3.3 simulink验证-传递函数

输入为50Hz,幅值为10的正弦波时,对于幅值:dq轴两个波形都是10;对于相位:d轴和输入波同相位,q轴滞后d轴90°。
输入为42.8Hz,幅值为10的正弦波时,对于幅值:d轴幅值为6.928,略小于计算值6.95,q轴幅值为8.094,略小于计算值8.19。
对于相位:d轴超前输入波形3ms,为46.22°(计算公式为2.93×0.001÷(1/42.8) ×360),略大于计算值45.4°。d轴滞后输入波形2.86ms,为-44.06°,略低于计算值-44.4°。
 文章来源:https://www.toymoban.com/news/detail-612954.html
文章来源:https://www.toymoban.com/news/detail-612954.html
2.3.4 simulink验证-C语言
-
https://www.cirmall.com/articles/31424/ ↩︎文章来源地址https://www.toymoban.com/news/detail-612954.html
到了这里,关于锁相环技术知识的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!