【图论】三种中心性 —— 特征向量、katz 和 PageRank-Toy模板网

这篇具有很好参考价值的文章主要介绍了【图论】三种中心性 —— 特征向量、katz 和 PageRank。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

维基百科：在图论和网络分析中，中心性指标为图中相应网络位置的节点分配排名或数值。中心性这一概念最初起源于社交网络分析，因此很多衡量中心性的术语也反映了其社会学背景。

不同中心性指标对 “重要” 的衡量方式不同，因此适用于不同的情形。katz 和 PageRank 都可以视为特征向量中心性的变体。

一、特征向量中心性（eigenvector centrality）

特征向量这一概念最早应该是在线性代数这门课程中接触到的，而取名中的特征向量也与它最初的概念相关，我们先回顾下什么是 “特征值” 和 “特征向量”。

1.1 线性代数中的特征向量

定义：设 A 是 n 阶方阵，若存在向量使得，则称 x 为 A 的特征向量，为 A 的特征值（严格定义请参考权威文献）。

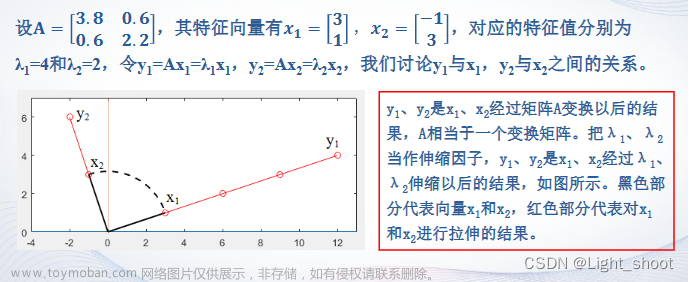
由定义可见，特征向量的本质是它与原矩阵相乘后，得到的矩阵与特征向量方向相同，仅存在缩放关系（即倍的缩放），该缩放比例称为特征值。进一步延伸，原矩阵无论乘上多少特征向量，其方向都是确定的。回顾一道求特征值和特征向量的简单例题，可以更好回忆相关概念，求的特征向量和特征值。

解得两个特征值 2 或 4，则应有

解得 $【图论】三种中心性 —— 特征向量、katz 和 PageRank,图论,图论$ ，因此可取特征值 2 的特征向量为

求特征值 4 的特征向量同理。

1.2 图论中的特征向量中心性

定义：图 G = (V, E)，定义其邻接矩阵 A，表示节点 v 和 t 不相连，表示节点 v 和 t 相连，则节点 v 的中心性 x 的分数计算式为

单纯看公式会觉得不好理解，结合具体的例子可以马上掌握，它在本质上是求图 G 邻接矩阵的特征向量，只不过在算法设计中，通常不是通过数学方式求得，而是采用迭代逼近的方式得到一个近似解。特征向量中心性的核心思想是，一个结点的邻居越重要，该结点就越重要。下面是一个经典的分析图，

【图论】三种中心性 —— 特征向量、katz 和 PageRank,图论,图论

各节点上的数字表示该结点的权重，以 5 作为节点 1，按顺时针标记各节点，且中心节点记为节点 5，则得到邻接矩阵为

第一轮迭代，邻接矩阵乘上各结点的分数

迭代完成后，各结点分数发生变化，效果为节点“吸收”了邻接节点的分数，邻接节点分数高的，迭代后分数就高。且经过多轮迭代后，各节点间的相对分数将不再发生变化，即收敛，仅存在绝对分数的缩放，此时我们就得到了最终的中心性分数矩阵，而该矩阵是邻接矩阵的特征向量。

【图论】三种中心性 —— 特征向量、katz 和 PageRank,图论,图论

二、katz 中心性

针对特征向量中心性无法用于有向图的不足，提出了 katz 中心性。

2.1 理解特征向量中心性的不足

每篇博客都说了，特征向量中心性不能用于有向图，但是为什么呢，这个结论怎么来的？

此处稍微探究下，我的理解不一定是对的，但特征向量中心性确实存在一些问题。首先观察上一节中邻接矩阵的特点，它是沿着主对角线对称的矩阵。这是可以理解的，无向图的连通性肯定是对称的。而特征向量中心性算法的本质是求邻接矩阵的特征向量，当邻接矩阵的性质发生变化时，特征向量必然会受影响。

在有向图中没有沿主对角线对称这一性质，那么对于只有出度、没有入度的节点，就存在一个致命问题，它的分数一直被出度节点吸收，而它自身分数将归零（以下图为例）。这显然是不合理的，这也是我理解的特征向量中心性计算方式不足的原因。

【图论】三种中心性 —— 特征向量、katz 和 PageRank,图论,图论

2.2 katz 中心性的改进思路

首先看看它的中心性计算公式，

$【图论】三种中心性 —— 特征向量、katz 和 PageRank,图论,图论$ .

或不考虑 k，

$【图论】三种中心性 —— 特征向量、katz 和 PageRank,图论,图论$ .

比较和特征向量中心性的不同，katz 引入了两个新的变量，分别是衰减因子和基本偏移量 。第一个求和号中的 k 表示 k-hop，即只考虑与节点 v 距离在 k 以内（通常以一个节点作为一个单位距离）的节点分数，该思路在特征向量中心性中也是可行的，只是在上一节中未列出来。k 取 1 时就表示只考虑直接相连的节点。

衰减因子随着 k 增大呈指数级减小，其设计思路是距离越近的节点对分数的影响应更大，反之应有衰减；
偏移量是为了避免出现 2.1 中讨论的分数归零现象；
可能较难理解，其实就是在 k 距离内的邻接矩阵，如 k = 1 就是与节点 v 直接相连的邻接矩阵，k = 2 就是与节点 v 隔一个节点相连的邻接矩阵。

通过例子理解先跳过，可以自己搜索具体的计算例子。

三、PageRank 中心性（PageRank centrality）

PageRank 应该是这三者中最出名的，主要用于谷歌的网页排序。

3.1 PageRank 中心性思想

一样先看 PageRank 的计算公式，

$【图论】三种中心性 —— 特征向量、katz 和 PageRank,图论,图论$ .

相比于 katz 中心性，可以发现它只是对每个节点的分数除以，即该节点的出度。这样调整的出发点是，katz 中心性中某个高分节点会较大地影响所有与其相邻的节点，结合社交网络的背景，比如名人的朋友并不都是名人。用出度稀释高分节点的分数可以避免部分节点拥有很强的影响力。文章来源地址https://www.toymoban.com/news/detail-615047.html

到了这里，关于【图论】三种中心性 —— 特征向量、katz 和 PageRank的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！